Метод Монте-Карло

2. Метод Монте-Карло

Различные методы и приборы для определения параметров и характеристик случайных процессов можно объединить в две группы. Первую группу составляют приборы для определения корреляционных функций (корреляторы), спектральных плотностей (спектрометры), математических ожиданий, дисперсий, законов распределения и прочих случайных процессов и величин.

Все приборы первой группы можно разделить на две подгруппы. Одни определяют характеристики записанных случайных сигналов за достаточно большое время, намного превышающее время реализации самого случайного процесса. Другие (они в последнее время вызывают наибольший интерес) позволяют получать характеристики случайного процесса оперативно, в такт с поступлением информации при натурных испытаниях новых систем управления, так как, пользуясь их показаниями, можно непосредственно изменять процесс управления и в ходе эксперимента наблюдать за результатами этих изменений.

Вторая группа содержит методы и приборы, предназначенные для исследования случайных процессов и главным образом систем управления, в которых присутствуют случайные сигналы, на универсальных цифровых и аналоговых вычислительных машинах. Иногда для таких исследований приходится создавать специализированные вычислительные машины цифрового, аналогового или чаще всего аналого-цифрового (гибридного) типа, так как существующие типовые машины не приспособлены для решения некоторых задач.

Широко применяется на практике метод Монте-Карло (метод статических испытаний). Его основная идея чрезвычайно проста и заключается по существу в математическом моделировании на вычислительной машине тех случайных процессов и преобразований с ними, которые имеют место в реальной системе управления. Этот метод в основном реализуется на цифровых и, реже, на аналоговых вычислительных машинах.

Можно утверждать, что метод Монте-Карло остаётся чистым методом моделирования случайных процессов, чистым математическим экспериментом, в известном смысле лишённым ограничений, свойственным другим методам. Рассмотрим данный метод применительно к решению различных задач управления.

2.1 Общая характеристика метода Монте-Карло

Как уже указывалось, идея метода Монте-Карло (или метода статистического моделирования) очень проста и заключается в том, что в вычислительной машине создаётся процесс преобразования цифровых данных, аналогичный реальному процессу. Вероятностные характеристики обоих процессов (реального и смоделированного) совпадают с какой-то точностью.

Допустим, необходимо вычислить математическое ожидание случайной величины X, подчиняющейся некоторому закону распределения F(x). Для этого в машине реализуют датчик случайных чисел, имеющий данное распределение F(x), и по формуле, которую легко запрограммировать, определяют оценку математического ожидания:

.

Каждое значение случайной величины x_i представляется в машине двоичным числом, которое поступает с выхода датчика случайных чисел на сумматор. Для статистического моделирования рассматриваемой задачи требуется N-кратное повторение решения.

Рассмотрим ещё один пример. Производится десять независимых выстрелов по мишени. Вероятность попадания при одном выстреле задана и равна p. Требуется определить вероятность того, что число попаданий будет чётным, т.е. 0, 2, 4, 6, 8, 10. Вероятность того, что число попаданий будет 2k, равна:

,

откуда искомая вероятность

(1)

Если эта формула известна, то можно осуществить физический эксперимент, произведя несколько партий выстрелов (по десять в каждой) по реальной мишени. Но проще выполнить математический эксперимент на вычислительной машине следующим образом. Датчик случайных чисел выдаст в цифровом виде значение случайной величины ξ, подчиняющейся равномерному закону распределения в интервале [0,1]. Вероятность неравенства ξ<p равна p, т.е.

P {ξ<p}=p.

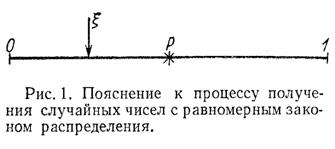
Для пояснения целесообразно обратиться к рис. 1, на котором весь набор случайных чисел представляется в виде точек отрезка [0,1]. Вероятность попадания случайной величины ξ, имеющей равномерное распределение в интервале [0,1], в интервал [0, p] (где ) равна длине этого отрезка, т.е. p. Поэтому на каждом такте моделирования полученное число ξ сравнивают с заданной вероятностью p. Если ξ<p, то регистрируется попадание в мишень, в противном случае – промах. Далее проводят серию из десяти тактов и подсчитывают чётное или нечётное число попаданий. При большом числе серий (100–1000) получается вероятность, близкая к той, которая определяется по формуле (1).

Различают две области применения метода Монте-Карло. Во-первых, для исследования на вычислительных машинах таких случайных явлений и процессов, как прохождение элементарных ядерных частиц (нейтронов, протонов и пр.) через вещество, системы массового обслуживания (телефонная сеть, система парикмахерских, система ПВО и пр.), надёжность сложных систем, в которых выход из строя элементов и устранения неисправностей являются случайными процессами, статистическое распознавание образов. Это – применение статистического моделирования к изучению так называемых вероятностных систем управления.

Этот метод широко применяется и для исследования дискретных систем управления, когда используются кибернетические модели в виде вероятностного графа (например, сетевое планирование с β-распределением времени выполнением работ) или вероятностного автомата.

Если динамика системы управления описывается дифференциальными или разностными уравнениями (случай детерминированных систем управления) и на систему, например угловую следящую систему радиолокационной станции воздействуют случайные сигналы, то статическое моделирование также позволяет получить необходимые точностные характеристики. В данном случае с успехом применяются как аналоговые, так и цифровые вычислительные машины. Однако, учитывая более широкое применение при статистическом моделировании цифровых машин, рассмотрим в данном разделе вопросы, связанные только с этим типом машин.

Вторая область применения метода Монте-Карло охватывает чисто детерминированные, закономерные задачи, например нахождение значений определённых одномерных и многомерных интегралов. Особенно проявляется преимущество этого метода по сравнению с другими численными методами в случае кратных интегралов.

При решении алгебраических уравнений методом Монте-Карло число операций пропорционально числу уравнений, а при их решении детерминированными численными методами это число пропорционально кубу числа уравнений. Такое же приблизительно преимущество сохраняется вообще при выполнении различных вычислений с матрицами и особенно в операции обращения матрицы. Надо заметить, что универсальные вычислительные машины не приспособлены для матричных вычислений и метод Монте-Карло, применённый на этих машинах, лишь несколько улучшает процесс решения, но особенно преимущества вероятностного счёта проявляются при использовании специализированных вероятностных машин. Основной идеей, которая используется при решении детерминированных задач методом Монте-Карло, является замена детерминированной задачи эквивалентной статистической задачей, к которой можно применять этот метод. Естественно, что при такой замене вместо точного решения задачи получается приближённое решение, погрешность которого уменьшается с увеличением числа испытаний.

Эта идея используется в задачах дискретной оптимизации, которые возникают при управлении. Часто эти задачи сводятся к перебору большого числа вариантов, исчисляемого комбинаторными числами вида N=. Так, задача распределения n видов ресурсов между отраслями для n>3 не может быть точно решена на существующих цифровых вычислительных машинах (ЦВМ) и ЦВМ ближайшего будущего из-за большого объёма перебора вариантов. Однако таких задач возникает очень много в кибернетике, например синтез конечных автоматов. Если искусственно ввести вероятностную модель-аналог, то задача существенно упростится, правда, решение будет приближённым, но его можно получить с помощью современных вычислительных машин за приемлемое время счёта.

При обработке больших массивов информации и управлении сверхбольшими системами, которые насчитывают свыше 100 тыс. компонентов (например, видов работ, промышленных изделий и пр.), встаёт задача укрупнения или эталонизации, т.е. сведения сверхбольшого массива к 100–1000 раз меньшему массиву эталонов. Это можно выполнить с помощью вероятностной модели. Считается, что каждый эталон может реализоваться или материализоваться в виде конкретного представителя случайным образом с законом вероятности, определяемым относительной частотой появления этого представителя. Вместо исходной детерминированной системы вводится эквивалентная вероятностная модель, которая легче поддаётся расчёту. Можно построить несколько уровней, строя эталоны эталонов. Во всех этих вероятностных моделях с успехом применяется метод Монте-Карло. Очевидно, что успех и точность статистического моделирования зависит в основном от качества последовательности случайных чисел и выбора оптимального алгоритма моделирования.

Задача получения случайных чисел обычно разбивается на две. Вначале получают последовательность случайных чисел, имеющих равномерное распределение в интервале [0,1]. Затем из неё получают последовательность случайных чисел, имеющих произвольный закон распределения. Один из способов такого преобразования состоит в использовании нелинейных преобразований. Пусть имеется случайная величина X, функция распределения вероятности для которой

.

Если y является функцией x, т.е. y=F(x), то  и поэтому . Таким образом, для получения последовательности случайных чисел, имеющих заданную функцию распределения F(x), необходимо каждое число y с выхода датчика случайных чисел, который формирует числа с равномерным законом распределения в интервале [0,1], подать на нелинейное устройство (аналоговое или цифровое), в котором реализуется функция, обратная F(x), т.е.

. (2)

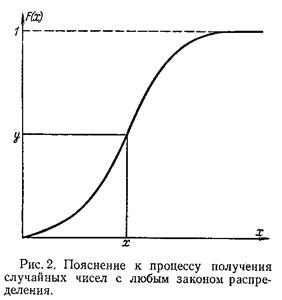
Полученная таким способом случайная величина X будет иметь функцию распределения F(x). Рассмотренная выше процедура может быть использована для графического способа получения случайных чисел, имеющих заданный закон распределения. Для этого на миллиметровой бумаге строится функция F(x) и вводится в рассмотрение другая случайная величина Y, которая связана со случайной величиной X соотношением (2) (рис. 2).

Так как любая функция распределения монотонно неубывающая, то

.

Отсюда следует, что величина Y имеет равномерный закон распределения в интервале [0,1], т. к. её функция распределения равна самой величине

.

Плотность распределения вероятности для Y

.

Для получения значения X берётся число из таблиц случайных чисел, имеющих равномерное распределение, которое откладывается на оси ординат (рис. 2), и на оси абсцисс считывается соответствующее число X. Повторив неоднократно эту процедуру, получим набор случайных чисел, имеющих закон распределения F(x). Таким образом, основная проблема заключается в получении равномерно распределённых в интервале [0,1] случайных чисел. Один из методов, который используется при физическом способе получения случайных чисел для ЭВМ, состоит в формировании дискретной случайной величины, которая может принимать только два значения: 0 или 1 с вероятностями

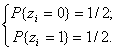
Далее будем рассматривать бесконечную последовательность z₁, z₂, z₃,… как значения разрядов двоичного числа ξ^* вида

Можно доказать, что случайная величина ξ^*, заключённая в интервале [0,1], имеет равномерный закон распределения

.

В цифровой вычислительной машине имеется конечное число разрядов k. Поэтому максимальное количество несовпадающих между собой чисел равно 2^k. В связи с этим в машине можно реализовать дискретную совокупность случайных чисел, т.е. конечное множество чисел, имеющих равномерный закон распределения. Такое распределение называется квазиравномерным. Возможные значения реализации дискретного псевдослучайного числа  в вычислительной машине с k разрядами будут иметь вид:

. (3)

Вероятность каждого значения (3) равна 2^-k. Эти значения можно получить следующим образом

.

Случайная величина  имеет математическое ожидание

.

Учитывая, что

и выражение для конечной суммы геометрической прогрессии

 , (4)

получаем:

. (5)

Аналогично можно определить дисперсию величины :

,

где

 

,

откуда

,

или, используя формулу (4), получаем:

. (6)

Согласно формуле (5) оценка  величины ξ^* получается смещённой при конечном k. Это смещение особенно сказывается при малом k. Поэтому вместо  вводят оценку

, (7)

где

.

Очевидно, что случайная величина ξ в соответствии с соотношением (3) может принимать значения

, i=0,1,2,…, 2^k-1

с вероятностью p=1/2^k.

Математическое ожидание и дисперсию величины ξ можно получить из соотношений (5) и (6), если учесть (7). Действительно,

;

.

Отсюда получаем выражение для среднеквадратичного значения в виде

. (8)

Напомним, что для равномерно распределённой в интервале [0,1] величины x имеем

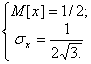
Из формулы (8) следует, что при  среднеквадратичное отклонение σ квазиравномерной совокупности стремится к . Ниже приведены значения отношения среднеквадратичных значений двух величин ξ и η в зависимости от числа разрядов, причём величина η имеет равномерное распределение в интервале [0,1] (табл. 1).

Таблица 1

k	2	3	5	10	15
σξ/ση	1,29	1,14	1,030	1,001	1,00

Из табл. 1 видно, что при k>10 различие в дисперсиях несущественно.

На основании вышеизложенного задача получения совокупности квазиравномерных чисел сводится к получению последовательности независимых случайных величин z_i (i=1,2,…, k), каждая из которых принимает значение 0 или 1 с вероятностью 1/2. Различают два способа получения совокупности этих величин: физический способ генерирования и алгоритмическое получение так называемых псевдослучайных чисел. В первом случае требуется специальная электронная приставка к цифровой вычислительной машине, во втором случае загружаются блоки машины.

При физическом генерировании чаще всего используются радиоактивные источники или шумящие электронные устройства. В первом случае радиоактивные частицы, излучаемые источником, поступают на счётчик частиц. Если показание счётчика чётное, то z_i=1, если нечётное, то z_i=0. Определим вероятность того, что z_i=1. Число частиц k, которое испускается за время Δt, подчиняются закону Пуассона:

.

Вероятность чётного числа частиц

.

Таким образом, при больших λΔt вероятность P{Z_i=1} близка к 1/2.

Второй способ получения случайных чисел z_i более удобен и связан с собственными шумами электронных ламп. При усилении этих шумов получается напряжение u(t), которое является случайным процессом. Если брать его значения, достаточно отстоящие друг от друга, так чтобы они были некоррелированы, то величины u(t_i) образуют последовательность независимых случайных величин. Обычно выбирают уровень отсечки a и полагают

причём уровень a следует выбрать так, чтобы

.

Также применяется более сложная логика образования чисел z_i. В первом варианте используют два соседних значения u(t_i) и u(t_i+1), и величина Z_i строится по такому правилу:

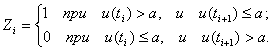
Если пара u(t_i) – a и u(t_i+1) – a одного знака, то берётся следующая пара. Требуется определить вероятность при заданной логике. Будем считать, что P {u(t_i)>a}=W и постоянная для всех t_i. Тогда вероятность события  равна по формуле событий A₁H_v. Здесь H_v – это вероятность того, что v раз появилась пара одинакового знака

u(t_i) – a; u(t_i+1) – a. (9)

Поэтому вероятность события A₁H_v

P{A₁H_v}=W (1-W) [W²+(1-W)²]^v.

Это – вероятность того, что после v пар вида (9) появилось событие A₁. Оно может появиться сразу с вероятностью W (1-W), оно может появиться и после одной пары вида (9) с вероятностью

W (1-W) [W²+(1+W)²]

и т.д. В результате

или

.

Отсюда следует, что если W=const, то логика обеспечивает хорошую последовательность случайных чисел. Второй способ формирования чисел z_i состоит в следующем:

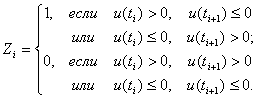
Пусть

W=P {u(t_i)>a}=1/2+ξ.

Тогда

P{Z_i=1}=2W (1-W)=1/2–2ξ².

Чем меньше ξ, тем ближе вероятность P{Z_i=1} к величине 1/2.

Для получения случайных чисел алгоритмическим путём с помощью специальных программ на вычислительной машине разработано большое количество методов. Так как на ЦВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно набрать конечное множество чисел, такие последовательности называются псевдослучайными. На самом деле повторяемость или периодичность в последовательности псевдослучайных чисел наступает значительно раньше и обусловливается спецификой алгоритма получения случайных чисел. Точные аналитические методы определения периодичности, как правило, отсутствуют, и величина периода последовательности псевдослучайных чисел определяется экспериментально на ЦВМ. Большинство алгоритмов получается эвристически и уточняется в процессе экспериментальной проверки. Рассмотрение начнём с так называемого метода усечений. Пусть задана произвольная случайная величина u, изменяющаяся в интервале [0,1], т.е. . Образуем из неё другую случайную величину

u_n=u [mod 2^-n], (10)

где u [mod 2^-n] используется для определения операции получения остатка от деления числа u на 2^-n. Можно доказать, что величины u_n в пределе при  имеют равномерное распределение в интервале [0,1].

По существу с помощью формулы (10) осуществляется усечение исходного числа со стороны старших разрядов. При оставлении далёких младших разрядов естественно исключается закономерность в числах и они более приближаются к случайным. Рассмотрим это на примере.

Пример 1. Пусть u = 0,10011101… = 1·1/2 + 0·1/2² + 0·1/2³ + 1·1/2⁴ + 1·1/2⁵ + 1·1/2⁶ + 0·1/2⁷ + 1·1/2⁸ + …

Выберем для простоты n=4. Тогда {u mod 2^-4} = 0,1101…

Из рассмотренного свойства ясно, что существует большое количество алгоритмов получения псевдослучайных чисел. При этом после операции усечения со стороны младших разрядов применяется стандартная процедура нормализации числа в цифровой вычислительной машине. Так, если усечённое слева число не умещается по длине в машине, то производится усечение числа справа.

При проверке качества псевдослучайных чисел прежде всего интересуются длиной отрезка апериодичности и длиной периода (рис. 3). Под длиной отрезка апериодичности L понимается совокупность последовательно полученных случайных чисел α₁, …, α_L таких, что α_iα_j при , , , но α_L+1 равно одному из α_k ().

Под длиной периода последовательности псевдослучайных чисел понимается T=L-i+1. Начиная с некоторого номера i числа будут периодически повторяться с этим периодом (рис. 3).

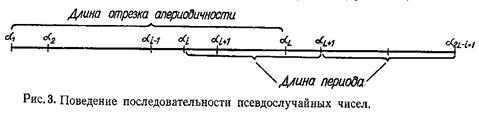
Как правило, эти два параметра (длины апериодичности и периода) определяются экспериментально. Качество совпадения закона распределения случайных чисел с равномерным законом проверяется с помощью критериев согласия.