Вступ
1. Теоретична частина
1.1 Постановка задачі
1.2 Використовувані методи і алгоритми
1.3 Вхідні та вихідні дані
2. Практична частина
2.1 Архітектура програми
2.2 Опис програми
2.3 Контрольний приклад
Висновок
Список використаної літератури
Додаток 1
Додаток 2
Додаток 3
Додаток 4
Вступ
Розвиток та значне поширення засобів обчислювальної техніки в останні роки послужило поштовхом для розробки програмного забезпечення різного рівня складності та різного за призначенням.
Для засвоєння вмінь та навичок розробки програмного забезпечення в процесі навчання вивчається предмет «Основи програмування та алгоритмічні мови». Курсовий проект є підсумком отриманих під час навчання знань.
Курсовий проект «Інтерполювання функцій за формулою Лагранжа» розроблений на алгоритмічній мові програмування з використанням модуля користувача для роботи з многочленами та математичних методів обробки інформації.
- в першому розділі виконується аналіз задачі, що вирішується, а саме: описується математичний аспект задачі, вичленяються базисні операції, які надалі оформляються як відносно незалежні частини програми (процедури і функції), приводяться вхідні дані.
- в другому розділі розкривається творчий процес рішення: логічне представлення даних, розробка алгоритму, розробка та опис програми.
Проект «Інтерполювання функцій за формулою Лагранжа» носить практичний характер і є досить актуальною.
1. Теоретична частина Постановка задачі
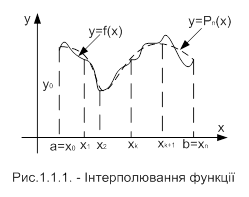
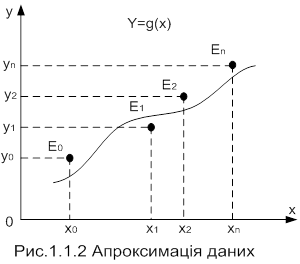
Нехай на відрізку [a;b] визначено певний клас функцій {P(x)}, наприклад, клас алгебраїчних многочленів, а в точках x0,x1,...,xn цього проміжку задано значення деякої функції y=f(x): y0=f(x0), y1=f(x1), ..., yn=f(xn). Наближену заміну функції f на відрізку [a;b] однією з функцій P(x) цього класу так, щоб функція P(x) в точках x0,x1,...,xn набувала тих самих значень, що й функція f, називають інтерполюванням або інтерполяцією. Точки x0, x1, ... ,xn називають вузлами інтерполювання, функцію P(x) - інтерполюючою функцією, а формулу f(x)»P(x), за допомогою якої обчислюють значення функції f у проміжку [a;b], - інтерполяційною формулою.
Якщо функція P(x) належить до класу алгебраїчних многочленів, то інтерполювання називається параболічним. Параболічне інтерполювання найзручніше, оскільки многочлени, які прості за формою і не мають особливих точок, можуть набувати довільних значень, їх легко обчислювати, диференціювати та інтегрувати.
Сформулюємо задачу параболічного інтерполювання: в n+1 різних точках x0, x1, ... ,xn задано значення функції f: y0=f(x0), y1=f(x1), ..., yn=f(xn) і треба побудувати многочлен
Pn(x)=a0xn+a1xn-1+...+an-1x+an
степеня n, який задовольняв би умови:
Pn(xi)=yi (i=0,1, . . . , n).
Задача має єдиний розв’язок. Многочлен Pn(x) називають інтерполяційним многочленом. Інтерполяційний многочлен єдиний, проте можливі різні форми його запису.
Інтерполяційний многочлен будують тоді, коли:
функцію задано таблично для деяких значень аргументу, а треба знайти її значення для значень аргументу, яких в таблиці нема.
функцію задано графічно, а треба знайти її наближений аналітичний вираз.
функцію задано аналітично, але її вираз досить складний і незручний для виконання різних математичних операцій.
При написанні даної роботи розглядалася задача побудови інтерполяційного многочлена.
Інтерполяційний многочлен Лагранжа має такий вираз:
Ln(x)=![]()
Многочлен Лагранжа зручно будувати у випадку рівновіддалених вузлів.
Використовувані методи і алгоритмиПри написанні представленої роботи використовувалися математичні методи, які відповідають основним операціям у кільці многочленів. На кільці многочленів визначеними є операції додавання, віднімання, множення та ділення з остачею. В ролі кільцевого нуля виступає многочлен нульового степеня f(x)=0, в ролі кільцевої одиниці – многочлен нульового степеня f(x)=1. В якості похідних операцій визначаються також: присвоєння, визначення степеня, обчислення значення, вводу та виводу многочлена на екран та в файл, множння многочлена на число. Якщо ми коректно означимо ці операції, то буде досить просто використовувати їх для обчислення коефіцієнтів шуканого многочлена та знаходження його значення для заданого значення х.
Вхідні та вихідні дані
Задане табличне представлення функції:
| x | 3 | 7 | 11 | 15 | 19 |
| y | 4 | 10 | 22 | 26 | 23 |
Методом інтерполяції Лагранжа знайти значення функції при x=13.
Щоб перевірити коректність роботи програми, яку потрібно створити, розв’яжемо цю задачу методами математичного пакету MathCad.
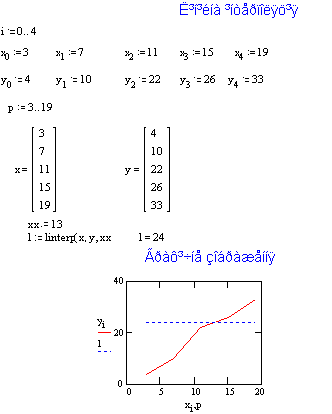
2. Практична частина 2.1 Архітектура програми
Розроблена програма складається з двох частин, кожна з яких записана у окремому файлі: модуль користувача bibl.tpu та прикладна програма lagr.pas. Прикладна програма використовує модуль користувача через механізм uses.
В бібліотеці підпрограм в розділі INTERFACE описані тип poli, що відповідає означенню многочлена (степеня не більше 100), тип mpoli - масиву многочленів, глобальні змінні zero та od, які відіграють роль відповідно нуля та одиниці кільця многочленів.
Там же описані наступні процедури і функції
* function stepin(a:poli):integer; (знаходження степеня многочлена)
* procedure riv(a:poli;var b:poli); (присвоєння одному многочлену значення іншого)
* procedure vvid(n:integer;var a:poli);( ввід многочлена)
* function poper(a:poli;m:integer):integer; (знаходження коефіцієнта многочлена, попереднього по відношенню до заданого)
* procedure vyvid(a:poli); (вивід многочлена згідно із загальноприйнятими стандартами)
* function maxi(n,m:integer):integer; (знаходження числа, більшого з двох)
* function mini(n,m:integer):integer; (знаходження числа, меншого з двох)
* procedure suma(a,b:poli;var c:poli); (знаходження суми двох многочленів)
* procedure nsuma(a:maspoli;n:integer;var c:poli); (знаходження суми n многочленів)
* procedure dobchy(a:poli;r:real;var c:poli); (добуток многочлена на скаляр)
* procedure pidvst(a:poli;n:integer;var c:poli);(підвищення степеня многочлена на n одиниць)
* procedure dobutok(a,b:poli;var c:poli);(знаходження добутку двох многочленів)
* procedure ndobutok(a:maspoli;n:integer;var c:poli);(знаходження добутку n многочленів)
* procedure mpoli(a:poli;m:integer;var c:poli); (знаходження m-го степеня многочлена)
* procedure polipoli(a,b:poli;var c:poli); (знаходження многочлена від многочлена)
* procedure dilen(a,b:poli;var c,c1:poli); (знаходження частки і остачі від ділення двох многочленів)
* procedure dyfer(a:poli;var b:poli); (знаходження похідної від многочлена)
* procedure integ(a:poli;var b:poli); (знаходження невизначеного інтеграла від многочлена)
Тексти процедур та функцій містяться в розділі IMPLEMENTATION.
Прикладна програма викликає з модуля користувача процедури: dobchy – добуток многочлена і числа, dobutok – добуток двох многочленів, suma – сума двох многочленів, vyvid – вивід многочлена на екран, fvyvid – вивід многочлена в файл, znach – обчислення значення многочлена. Крім того, ця програма використовує означений у модулі користувача тип poli (многочлен), а також змінні цього типу: zero (нуль), od (одиниця)
2.2 Опис програмиЛістинг модуля користувача міститься у додатку 2, лістинг прикладної програми – у додатку 3. Прикладна програма lagr.pas містить змінні типу integer та real, типу користувача poli, а ще використовує означену в модулі користувача змінну типу text.
До складу файлу входить директива компілятора $M, яка збільшує розмір стеку до максимально можливого.
Вивід результату роботи програми здійснюється у текстовий файл lagr.txt.
Схема алгоритму прикладної програми розміщена в додатку 1.
Запуск програми здійснюється:
- за допомогою операційної оболонки Norton Commander шляхом запуску lagr.exe (програма попередньо була прокомпільована з опцією Destination To Memory)
- з головного меню інтегрованого середовища TurboPascal шляхом вибору опції Run.
2.3 Контрольний прикладВ результаті виконання програми із заданими вхідними даними ми повинні одержати результат:
Многочлен Лагранжа
0.004x4-0.183x3+2.768x2-14.087x+25.958
Значення в точцi iнтерполяцii=24.898
Висновок
В даній курсовій роботі реалізована задача “Знаходження інтерполяційного многочлена Лагранжа”. Здійснено математичний опис задачі, постановку задачі та розробку програмного пакету згідно з постановкою.
Розроблено алгоритм поставленої задачі. Складено і налагоджено програму на мові Pascal. У процесі налагодження було одержано працездатний пакет програм.
Роботу пакету перевірено на контрольному прикладі, одержано результати, що співпадають з теоретичними.
Результат розробки оформлений у вигляді програмного проекту, що приводиться у додатку до курсової роботи.
Подальший розвиток роботи можливий у бік поліпшення зовнішнього інтерфейсу й адаптації програми до ширшого використання.
Список використаної літератури
А.Г. Курош “Курс высшей алгебры”, Государственное издательство физико-математической литературы, Москва, 1982.
Д.Б. Поляков, И.Ю. Круглов “Программирование в среде ТУРБО ПАСКАЛЬ”, Издательство МАИ, Москва, 1992.
Довгаль С.И., Литвинов Б.Ю., Сбитнев А.И. “Персональные ЭВМ. ТурбоПаскаль V6.0”, Информсистема сервис, Київ, 1993.
Додаток 1
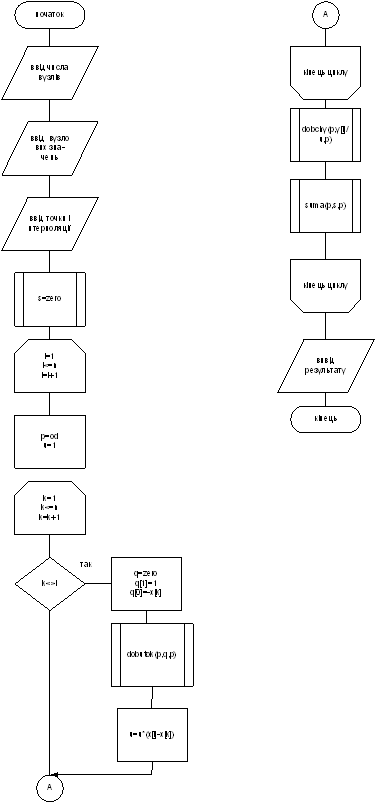
Рис. 1 - Блок-схема програми
Додаток 2
Лістинг модуля користувача
UNIT bibl; {Бiблiотека пiдпрограм по роботі з многочленами}
INTERFACE
uses crt;
TYPE
poli=array[0..100] of real;
type maspoli=array[1..20] of poli;
var zero,od:poli;
fi:text;
function stepin(a:poli):integer;
procedure riv(a:poli;var b:poli);
procedure vvid(n:integer;var a:poli);
function poper(a:poli;m:integer):integer;
procedure vyvid(a:poli);
procedure fvyvid(a:poli);
function maxi(n,m:integer):integer;
function mini(n,m:integer):integer;
function znach(a:poli;x:real):real;
procedure suma(a,b:poli;var c:poli);
procedure dobchy(a:poli;r:real;var c:poli);
procedure pidvst(a:poli;n:integer;var c:poli);
procedure dobutok(a,b:poli;var c:poli);
procedure dilen(a,b:poli;var c,c1:poli);
procedure zerod;
implementation
procedure zerod;
var i:integer;
begin
for i:=0 to 100 do begin zero[i]:=0;od[i]:=0;end;
od[0]:=1;
end;
function stepin(a:poli):integer;
{визначення степеня многочлена}
var i:integer;
begin
i:=100;
while ((a[i]=0) and (i>=0)) do i:=i-1;
stepin:=i;
end;
function znach(a:poli;x:real):real;
var i,n:integer;
s,st:real;
begin
s:=a[0];
st:=1;
n:=stepin(a);
for i:=1 to n do
begin
st:=st*x;
s:=s+st*a[i];
end;
znach:=s;
end;
procedure riv(a:poli;var b:poli);
{присвоення одному многочлену значення iншого}
var i:integer;
begin
for i:=0 to 100 do b[i]:=a[i];
end;
procedure vvid(n:integer;var a:poli);
{ввiд многочлена}
var i:integer;
begin
for i:=100 downto n+1 do a[i]:=0;
writeln('вводьте многочлен');
for i:=n downto 1 do
begin
write('x^',i:2,'*');
read(a[i]);
write('+');
end;
read(a[0]);
end;
function poper(a:poli;m:integer):integer;
{визначення молодшого на 1 коефiцiента многочлена пiсля m}
var i:integer;
begin
i:=m-1;
while (a[i]=0)and(i>=0) do i:=i-1;
poper:=i;
end;
procedure vyvid(a:poli);
{вивiд многочлена}
var i,n:integer;
begin
n:=stepin(a);
writeln;
if ((n>0)or(a[0]<>0)) then
begin
i:=n;
while ((i>=1)and(poper(a,i)>-1)) do
begin
if (a[i]<>0) then begin
if (i>1) then
write(a[i]:5:2,'x^',i:2)
else write(a[i]:5:2,'x');
if (a[poper(a,i)]>0) then write('+') ;
end;
i:=i-1;
end;
if (i>1) then write(a[i]:5:2,'x^',i:2)
else
if(i=1) then write(a[i]:5:2,'x')
else
write(a[i]:5:2);
end
else
write('0');
end;
procedure fvyvid(a:poli);
{вивiд многочлена в файл}
var i,n:integer;
begin
n:=stepin(a);
writeln(fi);
if ((n>0)or(a[0]<>0)) then
begin
i:=n;
while ((i>=1)and(poper(a,i)>-1)) do
begin
if (a[i]<>0) then begin
if (i>1) then
write(fi,a[i]:5:3,'x^',i:2)
else write(fi,a[i]:5:3,'x');
if (a[poper(a,i)]>0) then write(fi,'+') ;
end;
i:=i-1;
end;
if (i>1) then write(fi,a[i]:5:3,'x^',i:2)
else
if(i=1) then write(fi,a[i]:5:3,'x')
else
write(fi,a[i]:5:3);
end
else
write(fi,'0');
end;
function maxi(n,m:integer):integer;
begin
if(n>=m) then maxi:=n else maxi:=m;
end;
function mini(n,m:integer):integer;
begin
if(n<=m) then mini:=n else mini:=m;
end;
procedure suma(a,b:poli;var c:poli);
{сума 2 многочленiв}
var i,na,nb,nab,nba:integer;
begin
na:=stepin(a);
nb:=stepin(b);
nab:=maxi(na,nb);
for i:=100 downto nab+1 do c[i]:=0;
for i:=nab downto 0 do c[i]:=a[i]+b[i];
end;
procedure dobchy(a:poli;r:real;var c:poli);
{добуток скаляра на многочлен}
var i:integer;
begin
c:=zero;
for i:=0 to stepin(a) do
c[i]:=r*a[i];
end;
procedure pidvst(a:poli;n:integer;var c:poli);
{домноження многочлена на x^n)}
var i:integer;
begin
for i:=stepin(a)+n downto n do
c[i]:=a[i-n];
for i:=stepin(a)+n+1 to 100 do c[i]:=0;
for i:=0 to n-1 do c[i]:=0;
end;
procedure dobutok(a,b:poli;var c:poli);
{добуток 2 многочленiв}
var i:integer;
t,t1,t2:poli;
begin
t:=zero;
for i:=0 to stepin(b) do
begin
t1:=zero;
t2:=zero;
dobchy(a,b[i],t1);
pidvst(t1,i,t2);
suma(t,t2,t);
end;
c:=t;
end;
procedure dilen(a,b:poli;var c,c1:poli);
var n,m,i:integer;
t1,t2,t3,t4,t5:poli;
{дiлення многочленiв з остачею}
begin
riv(a,t4);
n:=stepin(a);
m:=stepin(b);
riv(zero,t3);
while n>=m do
begin
riv(zero,t5);
riv(zero,t1);
riv(zero,t2);
t5[n-m]:=a[n]/b[m];
suma(c,t5,c);
dobutok(t5,b,t1);
dobchy(t1,-1,t2);
suma(a,t2,a);
n:=stepin(a);
end;
dobutok(c,b,t3);
dobchy(t3,-1,t3);
suma(t4,t3,c1);
end;
Додаток 3
Лістинг програмного модуля
program lagr;
{$M 65520,0,655360}
{побудова многочлена Лагранжа}
Uses Crt,bibl;
{початок програми}
var i,j,k,n,m:integer;
s,p,q,p1:poli;
t,u,w:real;
x,y:array[1..20] of real;
begin
{створення кiльцевого нуля zero i кiльцевоi одиницi od}
zerod;
assign(fi,'lagr.txt');
rewrite(fi);
{ввiд вузлiв}
writeln('Введiть число вузлiв ');
readln(n);
for i:=1 to n do begin
writeln('Введiть x[',i,'] y[',i,']');
readln(x[i],y[i]); end;
writeln('Введiть точку iнтерполяцii '); readln(t);
writeln(' x y');
for i:=1 to n do writeln(x[i]:5:2,' ',y[i]:5:2);
writeln(fi,' x y');
for i:=1 to n do writeln(fi,x[i]:5:2,' ',y[i]:5:2);
writeln('Точка iнтерполяцii ',t:5:3);
writeln(fi,'Точка iнтерполяцii ',t:5:3);
s:=zero;
for i:=1 to n do
begin
p:=od;u:=1;
for k:=1 to n do
begin
if (k<>i) then
begin
q:=zero;q[1]:=1;q[0]:=-x[k];
dobutok(p,q,p); u:=u*(x[i]-x[k]);
end;
end;
dobchy(p,y[i]/u,p);
suma(s,p,s);end;
writeln('Многочлен Лагранжа '); writeln(fi,'Многочлен Лагранжа ');
vyvid(s); fvyvid(s);
writeln; writeln(fi);
w:=znach(s,t);
writeln('Значення в точцi iнтерполяцii=',w:5:3);
writeln(fi,'Значення в точцi iнтерполяцii=',w:5:3);
close(fi);
end.
Додаток 4
Результат роботи програми
x y
3.00 4.00
7.00 10.00
1.00 22.00
15.00 26.00
19.00 33.00
Точка iнтерполяцii 13.000
Многочлен Лагранжа
0.004x^ 4-0.183x^ 3+2.768x^ 2-14.087x+25.958
Значення в точцi iнтерполяцii=24.898
Похожие работы
... ефективності, що враховує затрати часу та пам'яті для його виконання, за даним методом. Третій розділ містить інструкція користувача, лістинг та опис програми і результати тестування. 1. Аналіз теоретичної бази інтерполювання функції 1.1 Постановка задачі інтерполяції Якщо задано певну довільну функцію на деякому проміжку , то обчислити її значення непросто. Для полегшення цієї задачі є ...
... інченно зменьшується. Таким чином, при достатньо великому обидві ці формули відтворюють шукане значення з довільним рівнем точності. Параболічне інтерполювання. Для наближеного обчислення інтеграла можно спробувати замінити функцію « близьким» до неї многочленом (3) і покласти Можно сказати, що тут – при обрахуванні площі – дана « крива» замінюється на « параболу - го порядку» ...
... ВНТУ. Виконавець – студент гр.. МП – 02 Твердохліб А.М. 2. Мета роботи. Метою роботи є розробка ефективного алгоритму та програми мовою Турбо Паскаль знаходження значення функції за допомогою інтерполяційної формули Бесселя. 3. Етапи виконання роботи. Зміст Строки виконання Чим закінчується етап 1.Отримання і узгодження завдання Розробка ТЗ 2–й тиждень Технічне завданя ...
... функцію задано аналітичнo, але її вираз досить складний і незручний для виконання різних математичних операцій (диференціювання, інтегрування тощо). 2 Розробка алгоритмів моделювання зміни температури термопари за допомогою чисельних методів на ЕОМ 2.1 Планування вхідних та вихідних даних Для розв’язання поставленої задачі потрібні певні вхідні данні, на основі яких будуть проводитись ...
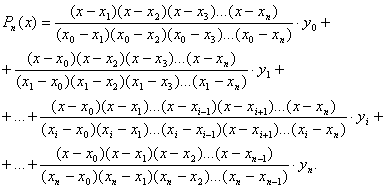

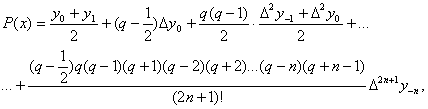


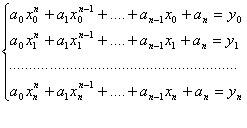
0 комментариев