Навигация
Дискретный канал связи без помех
2.1 Дискретный канал связи без помех
Если помехи в канале связи отсутствуют, то входные и выходные сигналы канала связаны однозначной, функциональной зависимостью.
При этом условная энтропия равна нулю, а безусловные энтропии источника и приемника равны, т.е. среднее количество информации в принятом символе относительно переданного равно
I (X, Y) = H(X) = H(Y); H (X/Y) = 0.
Если ХТ – количество символов за время T, то скорость передачи информации для дискретного канала связи без помех равна
 (6)
(6)
где V = 1/![]() – средняя скорость передачи одного символа.
– средняя скорость передачи одного символа.
Пропускная способность для дискретного канала связи без помех
![]() (7)
(7)
Т.к. максимальная энтропия соответствует для равновероятных символов, то пропускная способность для равномерного распределения и статистической независимости передаваемых символов равна:
![]() . (8)
. (8)
Первая теорема Шеннона для канала: Если поток информации, вырабатываемый источником, достаточно близок к пропускной способности канала связи, т.е.
![]() , где
, где ![]() - сколь угодно малая величина,
- сколь угодно малая величина,
то всегда можно найти такой способ кодирования, который обеспечит передачу всех сообщений источника, причем скорость передачи информации будет весьма близкой к пропускной способности канала.
Теорема не отвечает на вопрос, каким образом осуществлять кодирование.
Пример 1. Источник вырабатывает 3 сообщения с вероятностями:
p1 = 0,1; p2 = 0,2 и p3 = 0,7.
Сообщения независимы и передаются равномерным двоичным кодом (m = 2) с длительностью символов, равной 1 мс. Определить скорость передачи информации по каналу связи без помех.
Решение: Энтропия источника равна
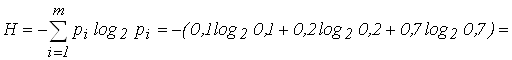
![]() [бит/с].
[бит/с].
Для передачи 3 сообщений равномерным кодом необходимо два разряда, при этом длительность кодовой комбинации равна 2t.
Средняя скорость передачи сигнала
V =1/2t = 500 [1/c].
Скорость передачи информации
C = vH = 500×1,16 = 580 [бит/с].
2.2 Дискретный канал связи с помехами
Мы будем рассматривать дискретные каналы связи без памяти.
Каналом без памяти называется канал, в котором на каждый передаваемый символ сигнала, помехи воздействуют, не зависимо от того, какие сигналы передавались ранее. То есть помехи не создают дополнительные коррелятивные связи между символами. Название «без памяти» означает, что при очередной передаче канал как бы не помнит результатов предыдущих передач.
При наличии помехи среднее количество информации в принятом символе сообщении – Y, относительно переданного – X равно:
![]() .
.
Для символа сообщения XTдлительностиT, состоящего из n элементарных символов среднее количество информации в принятом символе сообщении – YT относительно переданного – XT равно:
I(YT, XT) = H(XT) – H(XT/YT) = H(YT) – H(YT/XT) = n [H(Y) – H (Y/X). (9)
Для определения потерь в дискретном канале связи используется канальная матрица (матрица переходных вероятностей), позволяющая определить условную энтропию характеризующую потерю информации на символ сообщения.
Скорость передачи информации по дискретному каналу с помехами
равна:
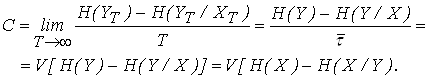 (10)
(10)
Пропускная способность дискретного канала при наличии помех равна максимально допустимой скорости передачи информации, причем максимум разыскивается по всем распределениям вероятностей p(x) на X и, поскольку, энтропия максимальна для равномерного распределения (для равновероятных символов сообщения), то выражение для пропускной способности имеет вид:
![]() . (11)
. (11)
Как видно из формулы, наличие помех уменьшает пропускную способность канала связи.
Пример. По каналу связи передаются сообщения, вероятности которых соответственно равны:
p(x1)=0,1; p(x2)=0,2; p(x3)=0,3; p(x4)=0,4.
Канальная матрица, определяющая потери информации в канале связи имеет вид:
|
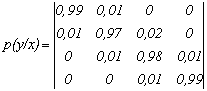 .
.
Определить:
1. Энтропию источника информации – H(X).
2. Безусловную энтропию приемника информации – H(Y).
3. Общую условную энтропию – H (Y/X).
4. Скорость передачи информации, если время передачи одного символа первичного алфавита t = 0,1 мс.
5. Определить потери информации в канале связи при передаче 500 символов алфавита.
6. Среднее количество принятой информации.
7. Пропускную способность канала связи.
Решение:
1. Энтропия источника сообщений равна

2. Вероятности появления символов на входе приемника
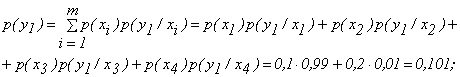
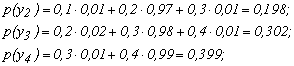
Проверка:
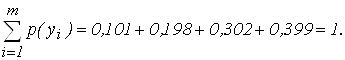
Энтропия приемника информации равна
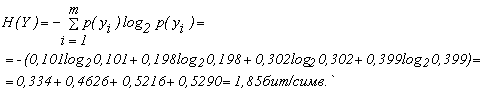
3. Общая условная энтропия равна

4. Скорость передачи информации равна:
![]()
=(1,85–0,132)/0,0001=17,18 Кбит/с.![]()
5. Потери информации в канале связи при передаче 500 символов алфавита равны:
![]() 500×0,132=66 бит.
500×0,132=66 бит.
6. Среднее количество принятой информации равно:
![]()
=500×(1,85–0,132)=859 бит.
7. Пропускная способность канала связи
![]() (2–0,132)/0,0001=18,68 Кбит/с.
(2–0,132)/0,0001=18,68 Кбит/с.
2.3 Пропускная способность бинарного, симметричного канала
Бинарным дискретным каналом называется канал, по которому передается только два элементарных дискретных символа (т.е. используется двоичный код).
Симметричным дискретным каналом называется канал, в котором. вероятности не зависят от передаваемых символов, т.е. вероятности правильной передачи одинаковы (p(x1)= p(x2)) и вероятности ошибочной передачи одинаковы (p(y1 /x2)= p(y2/x1)).
Рассмотрим двоичный дискретный канал, по которому передаются дискретные символы «0» и «1» (m=2). Если передаваемые символы независимы и равновероятны (p(x1)= p(x2)=1/2), то сигнал имеет максимальную энтропию (Hmax(X)=1), при этом p (1/0) = p (0/1).
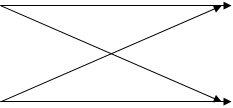
Если Pош – вероятность ошибки то 1‑Рош – вероятность правильного приема. Диаграмма передачи двоичных сигналов по симметричному калу приведена на рис. 2.
p(y1/ x1)= 1‑Рош
x1 не искажен y1
искажен p(y1/x2) =Pош
искажен p(y2/x1) =Pош
x2 не искажен y2
p(y2 / x2)= 1‑Рош
Рис. 2. Диаграмма переходных вероятностей симметричного канала
Условная энтропия для симметричного канала равна
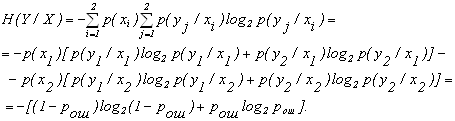
Пропускная способность для двоичного, симметричного канала
![]() (12)
(12)
Это уравнение Шеннона для симметричного двоичного канала.
Наличие ошибки приводит к уменьшению пропускной способности.
Так при pош = 0,01 пропускная способность равна C = 0,9/t = 0,9Cmax.
Основная теорема Шеннона о кодировании для дискретного канала с помехами: Для дискретного канала с помехами существует такой способ кодирования, который позволяет осуществлять безошибочную передачу информации, если производительность источника ниже пропускной способности
Пример. Определить скорость передачи по двоичному, симметричному каналу связи
Решение:
Составим таблицу вероятностей:
p(x0) = 0,5; p(y0/ x0) = 0,96;
p(x1) = 0,5; p(y1/ x0) = 0,04;
p(y0) = 0,5; p(y0/ x1) = 0,04;
p(y1) = 0,5; p(y1/ x1) = 0,96.
Пропускная способность для двоичного, симметричного канала

Похожие работы
... , чем 1,2 с) и возможного нарушения системы автоматического установления соединении Для предотвращения появления двойных скачков вводят определенные ограничения на использование спутниковых каналов. К настоящему времени спутниковая связь используется в двух основных областях - передача Циркулярной информации большому числу абонентов или широковещательная передача (ТВ- и звуковое вещание, передача ...
... искажениям принятых сообщений. Особенно сильно такие помехи проявляются в условиях одновременной работы мощных сторонних радиосредств. 2.2. Системы с временным уплотнением каналов. В многоканальных системах с временным разделением каналов (ВРК) канальные сигналы не перекрываются во времени, что обеспечивает их ортогональность. Рассмотрим один из способов формирования канальных сигналов ...
... этому адресу. Вызываемое устройство, организовав GPRS-сеанс и получив динамический IP-адрес, устанавливает TCP/IP-соединение с вызывающим устройством. 3. Анализ функционирования систем безопасности, использующих gsm каналы 3.1 Анализ помехоустойчивости и помехозащищённости gsm канала Помехи в радиоканале создаются как за счет искажений сигнала при его распространении, так и в результате ...
... 1.5 Уровни помех и линейных затуханий 1.5.1 Электрические помехи в каналах ВЧ связи по ВЛ Электрические помехи имеются в любом канале связи. Они являются основным фактором, ограничивающим дальность передачи информации из-за того, что сигналы, принимаемые приемником, искажаются помехами. Для того чтобы искажения не выходили за пределы, допустимые для данного вида информации, должно быть ...
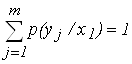
0 комментариев