Пропускная способность непрерывного канала связи

3.  Пропускная способность непрерывного канала связи

 

Непрерывный канал передачи информации содержит совокупность средств для передачи непрерывных сигналов, при этом вместо кодирующих и декодирующих устройств используются различного рода преобразователи (модуляция и т.д.). Входные и выходные сигналы в непрерывном канале связи представляют ансамбли непрерывных функций с соответствующими плотностями распределений вероятности.

Если на вход непрерывного канала связи поступает непрерывный сигнал X(t) длительностью T, то вследствие воздействия помех f(t) выходной сигнал Y(t) будет отличаться от входного. При этом количество информации в сигнале Y(t) о сигнале X(t) равно:

. (13)

Непрерывный сигнал, можно рассматривать как дискретный при. Он может быть представлен в виде решетчатой функции, при этом на приемной стороне по отдельным взятым отсчетам через интервал Dt может быть восстановлен исходный непрерывный сигнал.

Шаг квантования Dt = T/n, где n – число точек отсчета. В соответствии с теоремой Котельникова Dt = 1/2f_c, где f_c- частота среза а n = 2Tf_c – база сигнала.

При этом в выражении (13) для взаимной информации вместо разности энтропии можно записать разности соответствующих дифференциальных энтропий отдельных отсчетов

.

Пропускная способность непрерывного канала связи

 (14)

Для дискретного канала связи максимальное значение скорости передачи соответствует равновероятным символам алфавита. Для непрерывного канала связи, когда заданной является средняя мощность сигнала, максимальная скорость обеспечивается при использовании нормальных центрированных случайных сигнала.

Если сигнал центрированный (m_x= 0) т.е. без постоянной составляющей при этом мощность покоя равна нулю (P₀ = 0). Условие центрированности обеспечивает максимум дисперсии при заданной средней мощности сигнала

Если сигнал имеет нормальное распределение, то априорная дифференциальная энтропия каждого отсчета максимальна.

Поэтому при расчете пропускной способности непрерывного канала считаем, что по каналу передается непрерывный сигнал с ограниченной средней мощностью – P_c и аддитивная помеха (y = x+f) также с ограниченной средней мощностью – P_n типа белого (гауссова) шума.

Так как помеха аддитивна, то дисперсия выходного сигнала равна

.

Для того, чтобы энтропия была максимальна для сигнала с ограниченной мощностью, он должен быть гауссовым, при этом

.

Для того чтобы помеха была максимальна, она тоже должна быть гауссова

.

При этом пропускная способность непрерывного канала должна быть равна пропускной способности сигнала

. (15)

Таким образом, скорость передачи информации с ограниченной средней мощностью максимальна, если и сигнал, и помеха являются гауссовыми, случайными процессами.

Пропускную способность канала можно изменять, меняя ширину спектра сигнала – f_c его мощность – P_c. Но увеличение ширины спектра увеличиваетмощность помехи – P_n, поэтому соотношение между полосой пропускания канала и уровнем помех выбирается компромиссным путем.

Если распределение f(x) источника непрерывных сообщений отличается от нормального, то скорость передачи информации – С будет меньше. Используя, функциональный преобразователь, можно получать сигнал с нормальным законом распределения.

Обычно p_c/p_п >>1, при этом пропускная способность непрерывного канала равна С_п = F_кD_к. Связь между емкостью и пропускной способностью канала связи имеет вид V_к = T_к F_к D_к = T_к С_п.

Теорема Шеннона для непрерывного канала с шумом. Если энтропия источника непрерывных сообщений сколь угодно близка к пропускной способности канала, то существует метод передачи, при котором все сообщения источника будут переданы со сколь угодно высокой верностью воспроизведения.

Пример. По непрерывному каналу связи, имеющим полосу пропускания F_k = 1 кГц, передается полезный сигнал X(t), представляющий собой нормальный случайный процесс с нулевым математическим ожиданием и дисперсией = 4 мВ. В канале действует независимый от сигнала гауссов шум F(t) с нулевым математическим ожиданием и дисперсией = 1 мВ.

Определить:

– дифференциальную энтропию входного сигнала;

– дифференциальную энтропию выходного сигнала;

– условную дифференциальную энтропию;

– количество информации в одном непрерывном отсчете процесса Y(t) относительно отсчета X(t);

– скорость передачи информации по непрерывному каналу с дискретным временем;

– пропускную способность непрерывного канала связи;

– определить емкость канала связи, если время его работы T = 10 м;

– определить количество информации, которое может быть передано за 10 минут работы канала;

– показать, что информационная емкость непрерывного канала без памяти с аддитивным гауссовым шумом при ограничении на пиковую мощность не больше информационной емкости такого же канала при той же величине ограничения на среднюю мощность.

 

Решение:

Дифференциальная энтропия входного сигнала

= 3,05 бит/отсчет.

Дифференциальная энтропия выходного сигнала

 

=3,21 бит/отсчет.

Условная дифференциальная энтропия

 

= 2,05 бит/отсчет.

Количество информации в одном непрерывном отсчете процесса Y(t) относительно отсчета X(t) определяется по формуле

 

I (X, Y) = h(x) – h (x/y) = h(y) – h (y/x) = 3,21–2,05 = 1,16 бит/отсчет.

Скорость передачи информации по непрерывному каналу с дискретным временем определяется по формуле

 

=

= 2×10³× [3,21–2,05] = 2320 бит/с

Пропускная способность непрерывного канала с помехами определяется по формуле

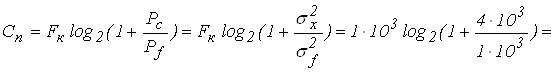
=2322 бит/с.

Докажем, что информационная емкость непрерывного канала без памяти с аддитивным гауссовым шумом при ограничении на пиковую мощность не больше информационной емкости такого же канала при той же величине ограничения на среднюю мощность.

Математическое ожидание для симметричного равномерного распределения

Средний квадрат для симметричного равномерного распределения

Дисперсия для симметричного равномерного распределения

При этом, для равномерно-распределенного процесса .

Дифференциальная энтропия сигнала с равномерным распределением

.

Разность дифференциальных энтропий нормального и равномерно распределенного процесса не зависит от величины дисперсии

 = 0,3 бит/отсч.

 

Таким образом, пропускная способность и емкость канала связи для процесса с нормальным распределением выше, чем для равномерного.

Определим емкость (объем) канала связи

 

V_k= T_kC_k= 10×60×2322 = 1,3932 Мбит.

Определим количество информации, которое может быть передано за 10 минут работы канала

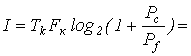10×60×2322=1,3932 Мбит.

Задачи

1. В канал связи передаются сообщения, составленные из алфавита x_1, x₂и x₃ с вероятностями p(x₁)=0,2; p(x₂₎=0,3и p(x₃)=0,5.

Канальная матрица имеет вид:

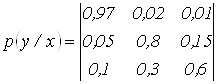 при этом .

 

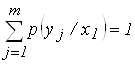Вычислить:

1. Энтропию источника информации H(X) и приемника H(Y).

2. Общую и условную энтропию H (Y/X).

3. Потери информации в канале при передаче к символов (к = 100).

4. Количество принятой информации при передаче к символов.

5. Скорость передачи информации, если время передачи одного символа t = 0,01 мс.

2. По каналу связи передаются символы алфавита x₁, x₂, x₃ и x₄ с вероятностями . Определить количество информации принятой при передаче 300 символов, если влияние помех описывается канальной матрицей:

.

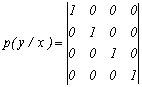3. Определить потери информации в канале связи при передаче равновероятных символов алфавита, если канальная матрица имеет вид

.

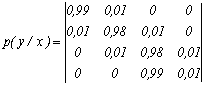Определить скорость передачи информации, если время передачи одного символа t = 0,001 сек.

4. Определить потери информации при передаче 1000 символов алфавита источника x₁, x₂ и x₃ с вероятностями p=0,2; p=0,1 и p()=0,7, если влияние помех в канале описывается канальной матрицей:

.

5. Определить количество принятой информации при передаче 600 символов, если вероятности появления символов на выходе источника X равны:  а влияние помех при передаче описывается канальной матрицей:

.

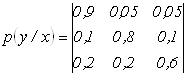6. В канал связи передаются сообщения, состоящие из символов алфавита , при этом вероятности появления символов алфавита равны:

Канал связи описан следующей канальной матрицей:

.

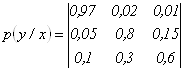Определить скорость передачи информации, если время передачи одного символа  мс.

7. По каналу связи передаются сигналы x₁, x₂ и x₃ с вероятностями p=0,2; p=0,1 и p()=0,7. Влияние помех в канале описывается канальной матрицей:

.

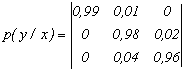Определить общую условную энтропию и долю потерь информации, которая приходится на сигнал x₁ (частную условную энтропию).

8. По каналу связи передаются символы алфавита x₁, x₂, x₃ и x₄ с вероятностями .

Помехи в канале заданы канальной матрицей

.

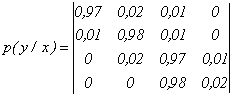Определить пропускную способность канала связи, если время передачи одного символа t = 0,01 сек.

Определить количество принятой информации при передаче 500 символов, если вероятности появления символов на входе приемника Y равны: , а влияние помех при передаче описывается канальной матрицей:

.

Список литературы

 

1    Гринченко А.Г. Теория информации и кодирование: Учебн. пособие. – Харьков: ХПУ, 2000.

2    Куприянов М.С., Матюшкин Б.Д. – Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. – СПб: Политехника, 1999.

3    Хемминг Р.В. Цифровые фильтры: Пер. с англ. / Под ред. А.М. Трахтмана. – М.: Сов. радио, 1980.

4    Сиберт У.М. Цепи, сигналы, системы: В 2-х ч. / Пер. с англ. – М.: Мир, 1988.

5    Скляр Б. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 1104 с.

6    Kalinin, V.I. Microwave & Telecommunication Technology, 2007. CriMiCo 2007. 17th International Crimean ConferenceVolume, Issue, 10–14 Sept. 2007 Page(s):233 – 234

7    Феер К. Беспроводная цифровая связь. Методы модуляции и расширения спектра. Пер. с англ. – М.: Радио и связь, 2000.

8    Игнатов В.А. Теория информации и передачи сигналов: Учебник для вузов. – 2-е изд., перераб. и доп. – М.: Радио и связь, 1991;