Навигация
Математические и алгоритмические основы решения задачи
14593
знака
2
таблицы
12
изображений
2. Математические и алгоритмические основы решения задачи
2.1 Понятие конечного автомата
Конечный автомат – в теории алгоритмов математическая абстракция, позволяющая описывать пути изменения состояния объекта в зависимости от его текущего состояния и входных данных, при условии, что общее возможное количество состояний конечно. Конечный автомат является частным случаем абстрактного автомата.
Существуют различные варианты задания конечного автомата. Например, конечный автомат может быть задан с помощью пяти параметров:
где:
Q – конечное множество состояний автомата;
q0 – начальное состояние автомата (
);
F – множество заключительных (или допускающих) состояний, таких что 
;
Σ – допустимый входной алфавит (конечное множество допустимых входных символов), из которого формируются строки, считываемые автоматом;
δ – заданное отображение множества 
во множество 
подмножеств Q:
(иногда δ называют функцией переходов автомата).
Автомат начинает работу в состоянии q0, считывая по одному символу входной строки. Считанный символ переводит автомат в новое состояние из Q в соответствии с функцией переходов. Если по завершении считывания входного слова (цепочки символов) автомат оказывается в одном из допускающих состояний, то слово «принимается» автоматом. В этом случае говорят, что оно принадлежит языку данного автомата. В противном случае слово «отвергается».
Конечные автоматы широко используются на практике, например в синтаксических, лексических анализаторах, и тестировании программного обеспечения на основе моделей.
2.2 Способы описания
Диаграмма состояний (или иногда граф переходов) – графическое представление множества состояний и функции переходов. Представляет собой нагруженный однонаправленный граф, вершины которого – состояния конечного автомата, дуги – переходы из одного состояния в другое, а нагрузка – символы, при которых осуществляется данный переход. Если переход из состояния q1 в q2 может быть осуществлен при появлении одного из нескольких символов, то над дугой должны быть надписаны все они.
Таблица переходов – табличное представление функции δ. Обычно в такой таблице каждой строке соответствует одно состояние, а столбцу – один допустимый входной символ. В ячейке на пересечении строки и столбца записывается действие, которое должен выполнить автомат, если в ситуации, когда он находился в данном состоянии на входе он получил данный символ.
2.3 Детерминированность
Конечные автоматы подразделяются на детерминированные и недетерминированные.
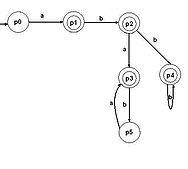http://ru.wikipedia.org/wiki/%D0%A4%D0%B0%D0%B9%D0%BB:%D0%94%D0%9A%D0%90.jpg
Рисунок 1 – Детерминированный http://ru.wikipedia.org/wiki/%D0%A4%D0%B0%D0%B9%D0%BB:%D0%94%D0%9A%D0%90.jpgконечный автомат
Детерминированным конечным автоматом (ДКА) называется такой автомат, в котором для каждой последовательности входных символов существует лишь одно состояние, в которое автомат может перейти из текущего.
Недетерминированный конечный автомат (НКА) является обобщением детерминированного. Недетерминированность автоматов достигается двумя способами.
1. Существуют переходы, помеченные пустой цепочкой ε (рисунок 2).
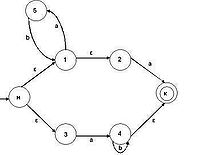
Рисунок 2 – Недетерминированный конечный автомат с пустыми переходами
2. Из одного состояния выходит несколько переходов, помеченных одним и тем же символом (рисунок 3).
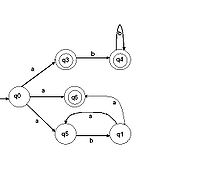
Рисунок 3 – Недетерминированный конечный автомат с несколькими переходами
Существует теорема, гласящая, что «Любой недетерминированный конечный автомат может быть преобразован в детерминированный так, чтобы их языки совпадали» (такие автоматы называются эквивалентными). Однако, поскольку количество состояний в эквивалентном детерминированном конечном автомате в худшем случае растёт экспоненциально с ростом количества состояний исходного недетерминированного конечного автомата, на практике подобная детерминизация не всегда возможна. Кроме того, конечные автоматы с выходом в общем случае не поддаются детерминизации.
В силу последних двух замечаний, несмотря на большую сложность недетерминированных конечных автоматов, для задач, связанных с обработкой текста, преимущественно применяются именно недетерминированные конечные автоматы.
Похожие работы
... с приглашением по запросу (в машинной графике)required parameter обязательный параметрrequired space обязательный пробел (в системах подготовки текстов)requirements specification 1. техническое задание 2. описание требований к программному средствуrerun перезапуск, повторный запускreschedule переупорядочивать очередь (о диспетчере операционной системы)reschedule interval период переупорядочения ...
... . Каждый язык программирования имеет четко заданные и специфицированные семантические соглашения, которые не могут быть проверены на этапе синтаксического разбора. Именно их в первую очередь проверяет семантический анализатор. Примерами таких соглашении являются следующие требования: · каждая метка, на которую есть ссылка, должна один раз присутствовать в программе; · каждый ...
... По теореме 9.3 в силу результатов шагов 3 и 8. (Шаг 10). Имеет место свойство (9.4) по теореме 9.5 в силу результатов шагов 1 и 9. Литература к лекции 9. 9.1. С.А. Абрамов. Элементы программирования. - М.: Наука, 1982. С. 85-94. 9.2. М. Зелковец, А. Шоу, Дж. Гэннон. Принципы разработки программного обеспечения. - М.: Мир, 1982. С. 98-105. Лекция 10. ТЕСТИРОВАНИЕ И ОТЛАДКА ПРОГРАММНОГО ...
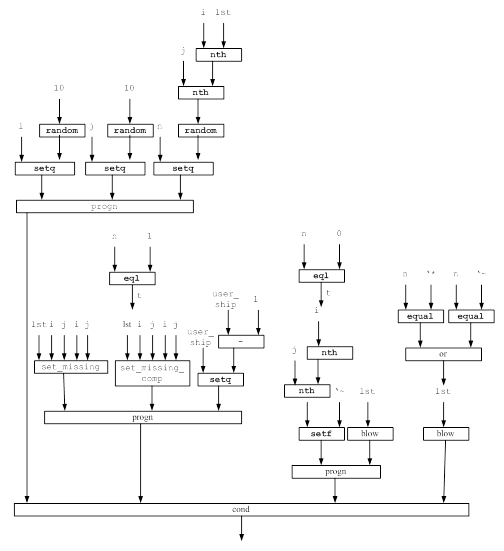
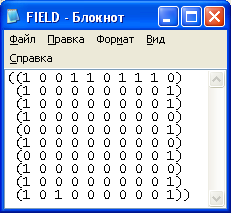
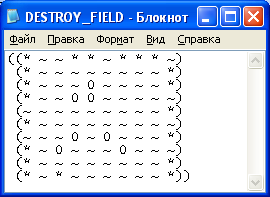
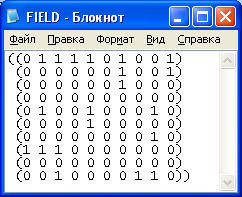
... характер, однако, в этом случае возникает проблема, связанная с понятием окончания игры. 1. Постановка задачи Задача заключается в разработке алгоритма, по которому компьютер сможет играть в «Морской бой» с максимальным качеством, и при этом не подглядывая расположение флота игрока. Дополнительное и очевидное условие: при каждой новой игре вне зависимости от размещения сил противника ...
0 комментариев