Навигация
1. Содержание: так как
![]() , B доминирует A.
, B доминирует A.
2. Равенство: так как
![]() , следовательно A не равно B.
, следовательно A не равно B.
3. Пересечение: ![]() .
.
4. Объединение: ![]() .
.
5. Разность: ![]() .
.
6. Произведение: ![]()
7. Отрицание: ![]() ,
,
![]() .
.
8. Дизъюнктивная сумма: ![]() .
.
Пример 2.
Пусть:
![]() ;
;
![]() .
.
Решение:
1. Содержание: так как
![]() , B доминирует A.
, B доминирует A.
2. Равенство: так как
![]() , следовательно A равно B.
, следовательно A равно B.
3. Пересечение:
![]() .
.
4. Объединение:
![]() .
.
5. Разность:
![]() .
.
6. Произведение
![]()
7. Отрицание:
![]() ,
,
![]() .
.
7. Дизъюнктивная сумма:
![]() .
.
2. Математические и алгоритмические основы решения задачи
2.1 Понятие нечеткого множества
Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество — понятие, введённое Лотфи Заде в 1965 г. в статье "Fuzzy Sets" (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1.
Под нечётким множеством A понимается совокупность
![]() ,
,
где— X универсальное множество, а ![]() — функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента нечёткому множеству A.
— функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента нечёткому множеству A.
Функция ![]() принимает значения в некотором вполне упорядоченном множестве M. Множество M называют множеством принадлежностей, часто в качестве M выбирается отрезок
принимает значения в некотором вполне упорядоченном множестве M. Множество M называют множеством принадлежностей, часто в качестве M выбирается отрезок ![]() . Если
. Если ![]() , то нечёткое множество может рассматриваться как обычное, чёткое множество.
, то нечёткое множество может рассматриваться как обычное, чёткое множество.
2.2 Операции над нечеткими множествами
Пусть A и B - нечеткие множества на универсальном множестве E.
2.2.1 Содержание
Говорят, что A содержится в B, если
![]() .
.
Обозначение: A М B.
Иногда используют термин "доминирование", то есть в случае если A М B, говорят, что B доминирует A.
2.2.2 Равенство
A и B равны, если
![]() .
.
Обозначение: A = B.
2.2.3 Пересечение
Пересечением нечётких множеств A и B называется наибольшее нечёткое подмножество, содержащееся одновременно в A и B:
![]() .
.
2.2.4 Объединение
![]()
- наименьшее нечеткое подмножество, которое включает как А, так и В, с функцией принадлежности:
![]()
2.2.5 Разность
![]() с функцией принадлежности:
с функцией принадлежности:
![]() .
.
2.2.6 Произведение
Произведением нечётких множеств A и B называется нечёткое подмножество с функцией принадлежности:
![]() .
.
2.2.7 Отрицание
Отрицанием множества A при ![]() называется множество
называется множество ![]() с функцией принадлежности:
с функцией принадлежности:
![]() .
.
Похожие работы
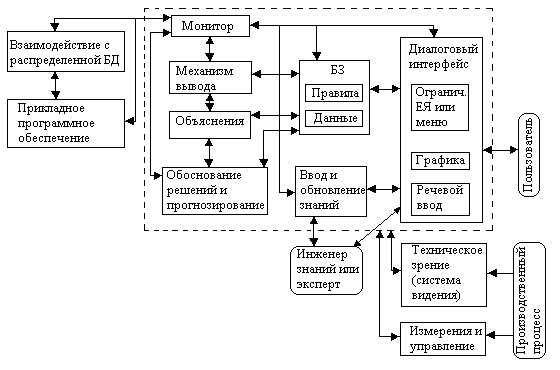
... распределения – сегодня одна из главных проблем производственных организаций. Таким образом, необходима автоматизация интеллектуальной деятельности человека в производственных системах управления. 2. Представление знаний в ПСИИ Важное место в теории искусственного интеллекта занимает проблема представления знаний, являющаяся, по мнению многих исследователей, ключевой. Что же представляют собой ...
... программирование [application programming] — разработка и отладка программ для конечных пользователей, например бухгалтерских, обработки текстов и т. п. Системное программирование [system programming] — разработка средств общего программного обеспечения, в том числе операционных систем, вспомогательных программ, пакетов программ общесистемного назначения, например: автоматизированных систем ...
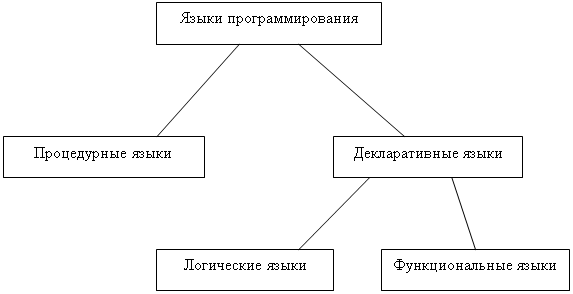
... . В частности: (8) Из (7) и (8) следует, что в M нет двух неравных натуральных чисел. Доказательство закончено. 3.2 Рекурсия Особое место для систем функционального программирования приобретает рекурсия, поскольку она позволяет учитывать значения функции на предыдущих шагах. С теоретической точки зрения рекурсивные определения являются теоретической основой всей современной ...
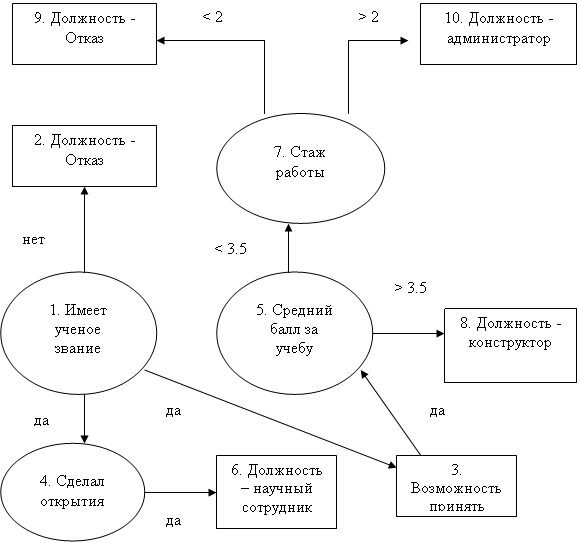
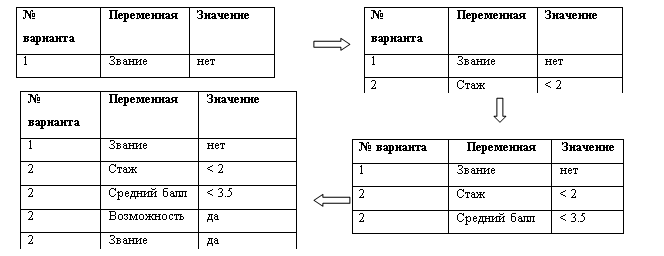
... систем электронной торговли; 5. Устранение промежуточных звеньев в системе интеграции организация - внешняя среда. 31. основные разделы искусственного интеллекта Одно из направлений информатики - интеллектуализация информационных систем. Интеллектуальные системы и технологии применяются для тиражирования профессионального опыта и решения сложных научных, производственных и экономических ...

0 комментариев