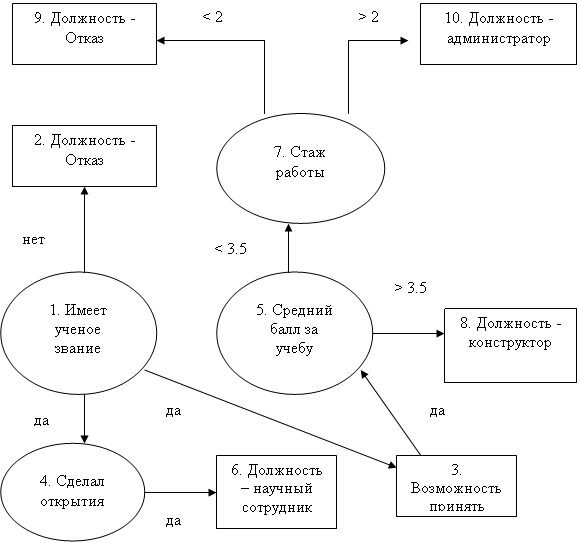
Навигация
2.2.8 Дизъюнктивная сумма
Дизъюнктивной суммой нечетких множеств A и B называется множество с функцией принадлежности:
![]() .
.
2.3 Наглядное представление операций над нечеткими множествами
Для нечетких множеств можно применить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значение mA(x), на оси абсцисс в произвольном порядке расположены элементы E. Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами.
Пусть A нечеткий интервал между 5 до 8 и B нечеткое число около 4, как показано на рисунке 1 и 2.
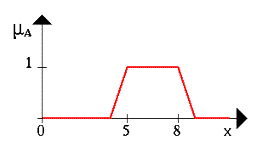
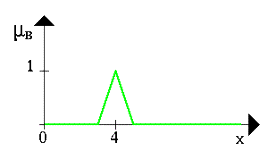
Рисунок 1. Множество A Рисунок 2. Множество B
Проиллюстрируем нечеткое множество между 5 AND 8 около 4 (синяя линия).
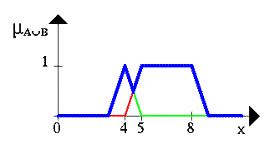
Рисунок 3. Пересечение множеств А и В
Нечеткое множество между 5 OR 8 около 4 показано на следующем рисунке (синяя линия).
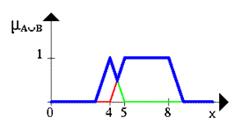
Рисунок 4. Объединение множеств А и В
Следующий рисунок иллюстрирует операцию отрицания. Синяя линия - это отрицание нечеткого множества A.
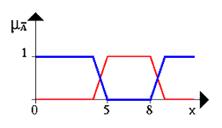
Рисунок 5. Отрицание множества А
На следующем рисунке заштрихованная часть соответствует нечеткому множеству A и изображает область значений А и всех нечетких множеств, содержащихся в A. Остальные рисунки изображают соответственно ![]() .
.




Рисунок 6. Множества ![]()
3. Функциональные модели и блок-схемы решения задачи
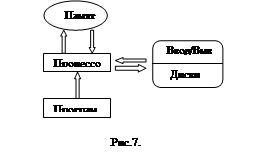
Функциональные модели и блок-схемы решения задачи представлены на рисунке 7 – 14.
Условные обозначения:
· X1 – первое множество;
· X2 – второе множество;
· X – множество.
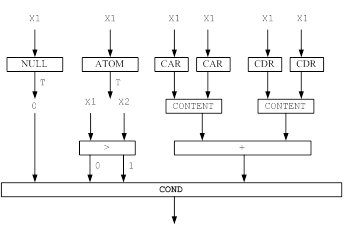
Рисунок 7 – Функциональная модель решения задачи для функции CONTENT (содержание)
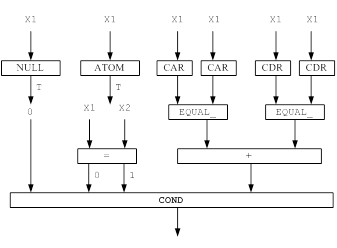
Рисунок 8 – Функциональная модель решения задачи для функции EQUAL_ (равенство)

Рисунок 9 – Функциональная модель решения задачи для функции CROSSING (пересечение)
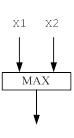
Рисунок 10 – Функциональная модель решения задачи для функции UNION (объединение)

Рисунок 11 – Функциональная модель решения задачи для функции SUBTR (разность)
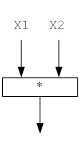
Рисунок 12 – Функциональная модель решения задачи для функции MULT (произведение)

Рисунок 13 – Функциональная модель решения задачи для функции ADDITION (отрицание)
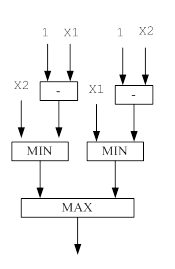
Рисунок 14 – Функциональная модель решения задачи для функции DIZ_SUMM (дизъюнктивная сумма)
4. Программная реализация решения задачи
;СОДЕРЖАНИЕ mA(x) < mB(x)
;РАВЕНСТВО mA(X) = mB(X)
;ПЕРЕСЕЧЕНИЕ min( mA(x), mB(x))
;ОБЪЕДИНЕНИЕ max(mA(x), m B(x))
;РАЗНОСТЬ А - B = АЗ с функцией принадлежности: mA-B(x) = mA З (x) = min( mA(x), 1 - m B(x))
;ПРОИЗВЕДЕНИЕ mA(x)* m B(x)
;ОТРИЦАНИЕ A^ = 1-mA(X)
;ДИЗЪЮНКТИВНАЯ СУММА АЕB = (А - B)И(B - А) = (А З ) И( З B) с функцией принадлежности:
;mA-B(x) = max{[min{m A(x), 1 - mB(x)}];[min{1 - mA(x), mB(x)}] }
;СОДЕРЖАНИЕ
;ЕСЛИ МНОЖЕСТВО A СОДЕРЖИТСЯ В МНОЖЕСТВЕ B - РЕЗУЛЬТАТОМ ФУНКЦИИ БУДЕТ 0
(DEFUN CONTENT (X1 X2)
(COND
((NULL X1) 0)
((ATOM X1) (IF (> X1 X2) 1 0))
(T (+ (CONTENT (CAR X1) (CAR X2)) (CONTENT (CDR X1) (CDR X2))))
)
)
;РАВЕНСТВО
;ЕСЛИ МНОЖЕСТВО A РАВНО МНОЖЕСТВУ B - РЕЗУЛЬТАТОМ ФУНКЦИИ БУДЕТ 0
(DEFUN EQUAL_ (X1 X2)
(COND
((NULL X1) 0)
((ATOM X1) (IF (EQUAL X1 X2) 0 1))
(T (+ (EQUAL_ (CAR X1) (CAR X2)) (EQUAL_ (CDR X1) (CDR X2))))
)
)
;ПЕРЕСЕЧЕНИЕ
(DEFUN CROSSING (X1 X2)
(MIN X1 X2)
)
;ОБЪЕДИНЕНИЕ
(DEFUN UNION (X1 X2)
(MAX X1 X2)
)
;РАЗНОСТЬ
(DEFUN SUBTR (X1 X2)
(MIN X1 (- 1 X2))
)
;ПРОИЗВЕДЕНИЕ
(DEFUN MULT (X1 X2)
(* X1 X2)
)
;ОТРИЦАНИЕ
(DEFUN ADDITION (X)
(- 1 X)
)
;ДИЗЪЮНКТИВНАЯ СУММА
(DEFUN DIZ_SUMM (X1 X2)
(MAX (MIN X1 (- 1 X2)) (MIN (- 1 X1) X2))
)
;РЕАЛИЗАЦИЯ ОПЕРАЦИЙ НАД МНОЖЕСТВАМИ
;С ПОМОЩЬЮ ОПИСАННЫХ РАННЕЕ ФУНКЦИЙ
;----------------------------------------------
;ПОЛУЧАЕМ МНОЖЕСТВА
(SETQ INPUT (OPEN " D:\MULTITUDE.TXT" :DIRECTION :INPUT))
(SETQ A (READ INPUT))
(SETQ B (READ INPUT))
(CLOSE INPUT)
;СОДЕРЖАНИЕ
(SETQ CONTENT_AB (IF (= (CONTENT A B)) "Mnowestvo A soderzitsya v mnowestve B" "Mnowestvo A NE soderzitsya v mnowestve B"))
;РАВЕНСТВО
(SETQ EQUAL_AB (IF (= (EQUAL_ A B) 0) "Mnowestvo A ravno B" "Mnowestvo A NE ravno B"))
;ПЕРЕСЕЧЕНИЕ
(SETQ CROSS_AB (MAPCAR 'CROSSING A B))
;ОБЪЕДИНЕНИЕ
(SETQ UNION_AB (MAPCAR 'UNION A B))
;ПРОИЗВЕДЕНИЕ
(SETQ MULT_AB (MAPCAR 'MULT A B))
;РАЗНОСТЬ
(SETQ SUBTR_AB (MAPCAR 'SUBTR A B))
;ОТРИЦАНИЕ
(SETQ A_ (MAPCAR 'ADDITION A))
(SETQ B_ (MAPCAR 'ADDITION B))
;ДИЗЪЮКТИВНАЯ СУММА
(SETQ DIZ_SUMM_AB (MAPCAR 'DIZ_SUMM A B))
;ЗАПИСЫВАЕМ РЕЗУЛЬТАТ ОПЕРАЦИЙ В ФАЙЛ
(SETQ OUTPUT (OPEN "D:\RESULT_OPERATIONS.TXT" :DIRECTION :OUTPUT))
(PRINT (LIST 'A A) OUTPUT)
(PRINT (LIST 'B B) OUTPUT)
(PRINT 'OPERATIONS OUTPUT)
(PRINT '------------------------- OUTPUT)
(PRINT (LIST 'CONTENT_AB CONTENT_AB) OUTPUT)
(PRINT (LIST 'EQUAL_AB EQUAL_AB) OUTPUT)
(PRINT (LIST 'CROSS_AB CROSS_AB) OUTPUT)
(PRINT (LIST 'UNION_AB UNION_AB) OUTPUT)
(PRINT (LIST 'MULT_AB MULT_AB) OUTPUT)
(PRINT (LIST 'SUBTR_AB SUBTR_AB) OUTPUT)
(PRINT (LIST 'A_ A_) OUTPUT)
(PRINT (LIST 'B_ B_) OUTPUT)
(PRINT (LIST 'DIZ_SUMM_AB DIZ_SUMM_AB) OUTPUT)
(TERPRI OUTPUT)
(CLOSE OUTPUT)
;КОНЕЦ
5. Пример выполнения программы
Пример 1.
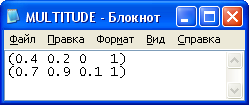
Рисунок 15 – Входные данные
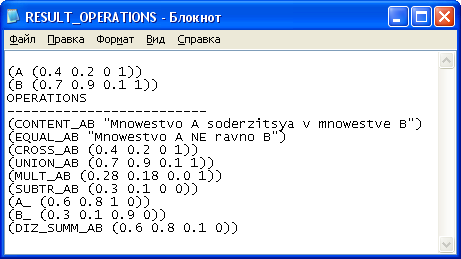
Рисунок 16 – Выходные данные
Пример 2.
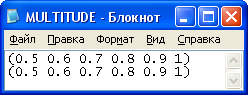
Рисунок 17 – Входные данные

Рисунок 18 – Выходные данные
Пример 3.

Рисунок 19 – Входные данные
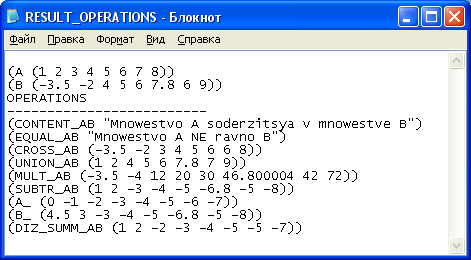
Рисунок 20 – Выходные данные
ЗАКЛЮЧЕНИЕ
Над нечеткими множествами можно производить различные операции, при этом необходимо определить их так, чтобы в частном случае, когда нечеткое множество является четким (обычным), эти операции переходили в обычные операции теории множеств, то есть операции над нечеткими множествами должны обобщать соответствующие операции над обычными множествами. При этом обобщение может быть реализовано различными способами, из-за чего какой-либо операции над обычными множествами может соответствовать несколько операций в теории нечетких множеств.
Итогом работы можно считать созданную функциональную модель реализации основных операций над нечеткими множествами. Созданная функциональная модель и ее программная реализация могут служить органической частью решения более сложных задач.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы
1. Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] / И.Н.Бронштейн, К.А.Семендяев. – М.: Наука, 2007. – 708 с.
2. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений [Электронный ресурс] / Заде Л. – М.: Мир, 1976. С. 166.
3. Кофман А. Введение в теорию нечетких множеств [Текст] / А.Кофман. – М.: Радио и связь, 1982. С. 432.
4. Круглов, В.В. Нечёткая логика и искусственные нейронные сети. [Текст] / В.В. Круглов, М.И. Дли, Р.Ю. Голунов. – М.: Питер, 2001. C. 224.
5. Нечеткое множество [Электронный ресурс] – Режим доступа: http://ru.wikipedia.org/wiki/Нечеткое_множество
6. Симанков, В.С. Основы функционального программирования [Текст] / В.С.Симанков, Т.Т.Зангиев, И.В.Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.
7. Степанов, П.А. Функциональное программирование на языке Lisp. [Электронный ресурс] / П.А.Степанов, А.В. Бржезовский. – М.: ГУАП, 2003. С. 79.
8. Хювенен Э. Мир Лиспа [Текст] / Э.Хювенен, Й.Сеппянен. – М.: Мир, 1990. – 460 с.
Похожие работы
... распределения – сегодня одна из главных проблем производственных организаций. Таким образом, необходима автоматизация интеллектуальной деятельности человека в производственных системах управления. 2. Представление знаний в ПСИИ Важное место в теории искусственного интеллекта занимает проблема представления знаний, являющаяся, по мнению многих исследователей, ключевой. Что же представляют собой ...
... программирование [application programming] — разработка и отладка программ для конечных пользователей, например бухгалтерских, обработки текстов и т. п. Системное программирование [system programming] — разработка средств общего программного обеспечения, в том числе операционных систем, вспомогательных программ, пакетов программ общесистемного назначения, например: автоматизированных систем ...
... . В частности: (8) Из (7) и (8) следует, что в M нет двух неравных натуральных чисел. Доказательство закончено. 3.2 Рекурсия Особое место для систем функционального программирования приобретает рекурсия, поскольку она позволяет учитывать значения функции на предыдущих шагах. С теоретической точки зрения рекурсивные определения являются теоретической основой всей современной ...
... систем электронной торговли; 5. Устранение промежуточных звеньев в системе интеграции организация - внешняя среда. 31. основные разделы искусственного интеллекта Одно из направлений информатики - интеллектуализация информационных систем. Интеллектуальные системы и технологии применяются для тиражирования профессионального опыта и решения сложных научных, производственных и экономических ...

0 комментариев