| Транспортна задача | ||||||||||||||||||||||||||||||||||||
|
Розв'язок задач лінійного програмування. Транспортна задача. Мета роботи: Набути навичок складання математичної моделі транспортної задачі та її реалізації з використанням табличного процесору Excel Задача: Чотири консервних заводи для виробництва продукції використовують сировину, яка надходить із трьох КСП.На кожен завод підприємств сировина може завозитися з будь-якого КСП. Потреби в сировині кожного із заводів,запаси сировини та тарифи перевезень наведені у таблиці. Скласти такий план перевезень, при якому загальна вартість перевезень є мінімальною.
Математична модель задачі буде мати наступний вигляд
Порядок виконання роботи
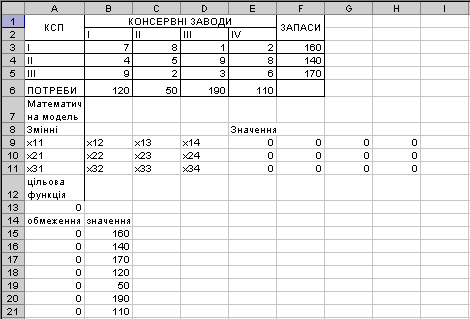
1.Створити новий текстовий документ за шаблоном Лабораторна робота і скопіювати до нього назву та мету лабораторної роботи, а також умови задачі. 3. Під таблицею увести до відповідних комірок математичну модель задачі: · використати для введення формули цільової функції СУММПРОИЗВ(); · використати для введення формул обмежень СУММ() (Мастер функций /Математические); · екран електронної таблиці буде мати наступний вид
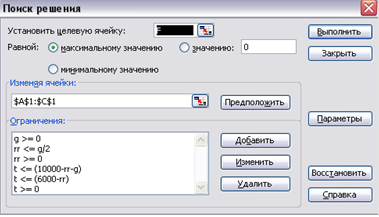
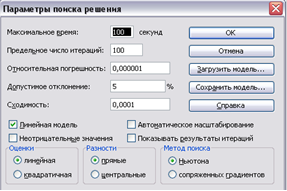
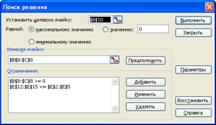
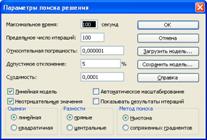
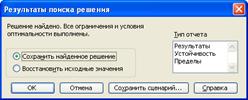
4. Викликати программу Поиск решения і розв'язати задачу 5.Результат розв'язку задачі 6.Скопіювати блок електронної таблиці із математичною моделлю та результатом розв'язку до документу Word із лабораторною роботою. 7.Зберегти робочу книгу табличного процесора Excel на сервері. 8.Зберегти документ Word на сервері.
1. Навести загальний вигляд розв'язку транспортної задачі. 2. Як викликати "Редактор формул"? 3. Як вибрати необхідну функцію? 4. Яким чином задаються обмеження? Завдання для самостійної роботи | ||||||||||||||||||||||||||||||||||||
| 2007-09-06 16:52:05 | ||||||||||||||||||||||||||||||||||||
| Самостійна робота "Транспортна задача" | ||||||||||||||||||||||||||||||||||||
Завдання до лабораторної роботи "Транспортна задача"
Завдання 1.
Створити новий документ на основі шаблону Самостійна робота та скопіювати до документу умови задачі.
Завдання 2. Записати математичну модель задачі (використовуючі редактор формул).
Завдання 3.
Знайти розв"язок задачі із використанням задачі пошуку рішень табличного процесора Excel. У процесі запису математичної моделі задачі до комірок ЕТ викорисовувати функцію СУММПРОИЗВ()
Завдання 4.
Зберегти документи Word і Excel у паці Самостійна робота.
Задача
До піприємства харчової галузі надходить сировина із різних КСП. Сировина надходить із будь-якого КСП на будь-яке підприємство. Потреби, запаси і тарифи перевезень наведені у таблиці. Скласти Оптимальний план перевезень (із найменшими витиратами).
| Варiант 1 | ||||
| КСП | Харчові підприємства | Запаси | ||
| І | ІІ | ІІІ | ||
| І | 4 | 1 | 10 | 200 |
| ІI | 2 | 3 | 2 | 300 |
| ІІІ | 1 | 2 | 5 | 100 |
| Потреби | 150 | 250 | 200 | |
Математична модель задачі буде мати наступний вигляд
F(x)=4 x11+x12+10 x13+2 x21+3 x22+2 x23+x31+2 x32+5 x33
| x11+x12+x13 = 200 |
| x21+x22+x23 = 300 |
| x31+x32+x33 = 100 |
| x11+x21+x31 = 150 |
| x12+x22+x32 = 250 |
| x13+x23+x33 = 200 |
| Математична модель задачі | |||||||
| Змінні | Значення | ||||||
| x11 | x12 | x13 | 0 | 0 | 200 | ||
| x21 | x22 | x23 | 50 | 250 | 0 | ||
| x31 | x32 | x33 | 100 | 0 | 0 | ||
Цільова функція
2950
| Обмеження | Значення |
| 200 | 200 |
| 300 | 300 |
| 100 | 100 |
| 150 | 150 |
| 250 | 250 |
| 200 | 200 |
| КСП | Харчові підприємства | Запаси | ||
| І | ІІ | ІІІ | ||
| І | 0 | 0 | 200 | 200 |
| ІI | 50 | 250 | 0 | 300 |
| ІІІ | 100 | 0 | 0 | 100 |
| Потреби | 150 | 250 | 200 | |
1.ЗАГАЛЬНИЙ ВИГЛЯД РОЗВ’ЯЗКУ ТРАНСПОРТНОЇ ЗАДАЧІ:
Математична модель задачі буде мати наступний вигляд
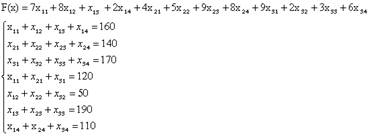
1. Порядок виконання
1. 2. Як викликати "Редактор формул"?
Вставка – обьект - microsoft eguation 3.0
1. 3. Як вибрати необхідну функцію?
Вставка – функція
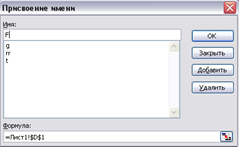
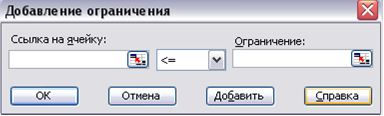
4. Яким чином задаються обмеження?
Обмеження задаються за допомогою
“ПОИСК РЕШЕНИЯ” – ОГРАНИЧЕНИЯ - ДОБАВИТЬ
Похожие работы
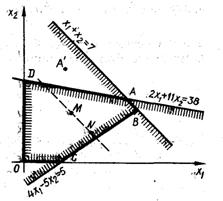
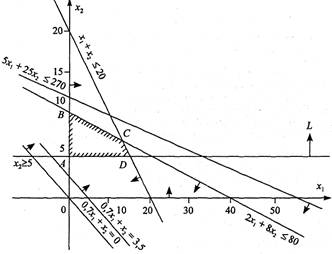
... , а при більшому числі змінних - взагалі неможливим. Незважаючи на це, розгляд графічного методу дасть змогу зробити висновки, що послужать основою для розробки загального методу розв’язання задач лінійного програмування[2]. Перший крок при використанні графічного методу полягає в поданні області допустимих розв’язків, у якій водночас задовольняються всі обмеження моделі. Нехай шукана область ( ...
... пошуку. Побудований нами приклад показав, що для рішення задач із вимогою цілочисленності необхідно розглянути особливі методи оптимізації; і, крім того, ми бачимо, що оптимальне рішення задач цілочисленного програмування не обов'язково належить границі багатогранника (багатокутника) умов, що було характерно для задач лінійного програмування. 2. Теоретичні основи методів відсікання Запишемо ...
... розвиток як математична теорія лінійного і нелінійного програмування, так і додаток її методів до дослідження різних економічних проблем. У 1949 р. американським математиком Дж. Данцигом (GB Dantzig) був опублікований симплекс-метод - основний метод рішення задач лінійного програмування. Термін «лінійне програмування» вперше з'явився в 1951 р. в роботах Дж. Данцига і Т. Купманса. При всьому ...
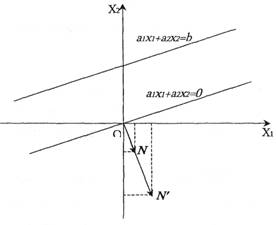
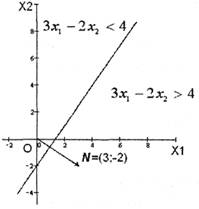
... зумовлюється метою, якої хочуть досягти даною геометричною інтерпретацією та особливостями структури самої задачі, в тому числі й формою її представлення. Для геометричної інтерпретації візьмемо основну задачу лінійного програмування у другій стандартній формі. Для наочності розглянемо найпростіший випадок, коли в системі обмежень (26) і цільовій функції (25) є лише дві змінних, Розглянемо розв' ...
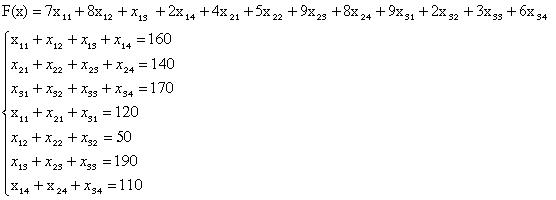

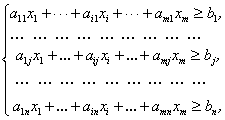
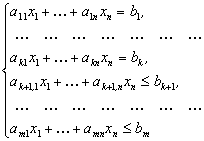
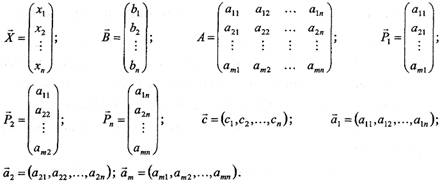
0 комментариев