Навигация
Стандартна задача лінійного програмування
Історія предмета включає в себе, з одного боку, історію математичних джерел та методів, а з другого — історію застосування цих методів у прикладних галузях, насамперед в економіці.
Як найпершу економічну модель, що містила деякі найпростіші ідеї лінійного програмування, слід назвати „Економічні таблиці" лейб-медика короля Людовика XV Ф. Кене, складену ним близько 1758 р., в якій було запропоновано кількісну модель національної економіки. У цій праці він поділив економіку Франції на три частини:
1) виробничий сектор, включаючи великих власників землі;
2) сектор торгівлі, що складався із купців та ремісників;
3) сектор нерухомості, що включав майно дворянства, церкви та королів.
Математичні моделі використовувались з ілюстративними і дослідницькими цілями також А. Смітом (класична макроекономічна модель), Д. Рікардо (модель міжнародної торгівлі).
З відомих нам математичних робіт основному методу лінійного програмування - симплексному - передували праці Ш. Фур'є (1823 p.), який розглядав задачу визначення найменшого максимального відхилення в розв'язках систем рівнянь. Ним ця задача була зведена до знаходження найнижчої точки многогранника n-вимірного простору, яку визначали послідовним перебором усіх вершин многогранника. Ідея Фур'є і лягла в основу симплексного методу.
У XIX сторіччі великий внесок у моделювання ринкової економіки внесла математична школа (Л. Вальрас, О. Курно, В. Парето, Ф. Еджворт). В 1874 Р- Л. Вальрас запропонував складну математичну модель економіки, що містила технологічні коефіцієнти.
У XX сторіччі математичні методи моделювання застосовувались дуже широко, з їх використанням зв'язані практично всі роботи, визначені Нобелевською премією в економіці (Д. Хіте, Р. Солоу, В. Леонтьев, П. Самуєльсон). Розвиток мікроекономіки, макроекономіки, прикладних дисциплін зв'язано з усе більш високим рівнем їх формалізації. Основу для цього заклав прогрес в області прикладної математики - теорії ігор, математичного програмування, математичної статистики.
У1926 р. в СРСР був опублікований баланс народного господарства, що містив усі основні ідеї і риси моделі міжгалузевого балансу, яка є методом математичного аналізу міжгалузевих економічних зв'язків.
Ґрунтуючись на цих ідеях, американський економіст В. Леонтьев створив кількісну модель американської економіки, яка давала можливість простежити вплив урядової політики і тенденції у сфері закупок на цілий ряд промислових галузей, тісно взаємозв'язаних між собою.
Вперше задачу оптимізації плану перевезень з метою мінімізації їх сумарного кілометражу було поставлено в роботі радянського економіста А. Н. Толстого в 1930 р.
Угорський математик Б. Егерварі в 1931р. сформулював задачу оптимального вибору і дав метод її розв'язування, що дістав назву угорського методу.
Проте, справжнім початком математичного (лінійного програмування) в його сучасному вигляді слід вважати праці радянського математика академіка Л. В. Канторовича, який у 1939 р. зайнявшись плануванням роботи агрегатів фанерної фабрики, розв'язав декілька задач: про найкраще завантаження обладнання, про розкрій матеріалів з найменшими втратами, про вантажі по декільком видам транспорту та ін. Л.В. Канторович сформулював новий клас умовно-екстремальних задач і запропонував універсальний метод їх розв'язування, що поклало початок новому напряму прикладної математики - лінійному програмуванню.
Значний внесок у формування і розвиток математичного програмування внесли зарубіжні вчені Р. Акоф, Р. Белман, Г. Данциг, Г. Кун, Дж. Нейман, Т. Сааті, Р. Черчмен, А. Кофман. Так, наприклад, американський математик P. Белман заклав основи динамічного програмування (І954)-
У 1960-80-і роки економіко-математичний напрямок на Україні був пов'язаний в основному зі спробами формально описати „систему оптимального функціонування соціалістичної економіки". Будувалися багаторівневі системи моделей народногосподарського планування, оп-тямізаційні моделі галузей і підприємств. Зараз важливою задачею є моделювання процесів перехідного періоду.
1. Приклади задач математичного програмування
Багато різних за реальним змістом задач лінійного програмування мають подібну математичну структуру, певні особливості якої можна успішно використати при побудові алгоритмів розв'язування цих задач. Виходячи з цієї подібності, всі задачі лінійного програмування часто поділяють на дві великі групи. Типовими задачами першої групи є задачі на добір оптимальної суміші сплавів та на складання оптимального раціону. За ними закріпилась назва задачі про раціон.
Типовими задачами другої групи є транспортна задача і задача про оптимальний добір. Ці задачі називаються задачами розподільчого типу.
Задача на складання суміші сплаву. Нехай потрібно виплавити новий сплав, що містить а% свинцю, b% цинку і d% олова. Припустимо, що в розпорядженні підприємства є и різних сплаві, кожний з яких містить ![]() свинцю,
свинцю,![]() цинку і
цинку і ![]() олова і може бути використаний для виробництва нового сплаву. Ціна одного кілограма
олова і може бути використаний для виробництва нового сплаву. Ціна одного кілограма ![]() -го сплаву дорівнює
-го сплаву дорівнює ![]() . Завдання полягає в тому, щоб визначити, яку кількість кожного сплаву потрібно затратити на кожний кілограм нового сплаву, щоб він був найдешевшим. Позначивши шукані величини xj, одержимо цільову функцію
. Завдання полягає в тому, щоб визначити, яку кількість кожного сплаву потрібно затратити на кожний кілограм нового сплаву, щоб він був найдешевшим. Позначивши шукані величини xj, одержимо цільову функцію
![]() (1)
(1)
яку слід мінімізувати при такій системі обмежень
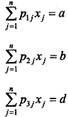 (2)
(2)
![]() (3)
(3)
![]()
Задача про оптимальний добір в племінній справі. Велике значення в підвищенні ефективності тваринництва має племінна робота. Одним з найважливіших завдань при цьому є правильний добір сам-ця-плідника до самок маточного поголів'я. В умовах штучного запліднення, яке тепер є основним, за одним самцем закріплюється ціла група маток, кількістю від кількох сотень до кількох тисяч. Нехай, у певному господарстві, чи зоні, що включає групу господарств, усе маточне поголів'я розподілене на N груп згідно з деякою сукупністю ознак, які визначають продуктивність нащадків, наприклад, належність до однієї породи та лінії, умови утримання, годівлі тощо. Позначимо кількість кожної групи ![]() , так що
, так що ![]() - загальне число маток. Припустимо, що кожний з наявних у господарстві т самців-плідників випробуваний на певній кількості маток кожної
- загальне число маток. Припустимо, що кожний з наявних у господарстві т самців-плідників випробуваний на певній кількості маток кожної ![]() -ї групи, в результаті чого добуто відповідні статистичні (вибіркові) середні продуктивної якості нащадків кожного і-го самця по кожній
-ї групи, в результаті чого добуто відповідні статистичні (вибіркові) середні продуктивної якості нащадків кожного і-го самця по кожній ![]() -й групі маток. Позначимо ці величини
-й групі маток. Позначимо ці величини ![]() , а максимальну здатність
, а максимальну здатність ![]() -го самця-плідника
-го самця-плідника ![]() в рік - через
в рік - через ![]() , що означає максимально можливе число маток, запліднюваних
, що означає максимально можливе число маток, запліднюваних ![]() -м самцем. Тепер задачу лінійного програмування можемо сформулювати так. Знайти цілочислову матрицю
-м самцем. Тепер задачу лінійного програмування можемо сформулювати так. Знайти цілочислову матрицю
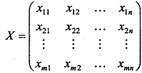
таку, щоб лінійна форма
![]() (4)
(4)
набувала максимального значення при системі умов:
![]() (5)
(5)
![]() (6)
(6)
![]() ' (7)
' (7)
де ![]() — означає кількість маток
— означає кількість маток ![]() -ї групи, що запліднюються і-м самцем.
-ї групи, що запліднюються і-м самцем.
Наведемо приклади задач нелінійного програмування.
Задача оптимального вибору факторів виробничої функції. Нехай, z— кількість деякого продукту, на виробництво якого витрачаються певні ресурси в кількостях ![]() . При цьому, якщо вартість одиниці
. При цьому, якщо вартість одиниці ![]() -го ресурсу cj, то загальні витрати виробництва
-го ресурсу cj, то загальні витрати виробництва
![]() (8)
(8)
Нехай, відома також залежність величини z, вираженої в натуральних чи вартісних одиницях, від кількостей використаних в процесі виробництва ресурсів xj, які виступають як фактори виробництва,
![]() (9)
(9)
Вид та параметри функції (9) залежать від технології виробництва і, як правило, встановлюються статистичними методами. Найбільше застосування дістала виробнича функція Коббо-Дугласа
![]() (9a)
(9a)
Зрозуміло, що
![]() (10)
(10)
В даному випадку можна сформулювати дві взаємозв'язаних задачі математичного програмування протилежного змісту.
Перша задача: при заданому об'ємі загальних витрат на виробництво продукції w=const , тобто при заданих асигнуваннях максимізувати випуск продукції z→max.
Друга задача: при заданому об'ємі виробництва даної продукції z=const мінімізувати величину загальних витрат на її виробництво w→min.
Цільовою функцією першої задачі є функція (9), а обмеженнями — співвідношення (8), (10); для другої задачі цільовою функцією являється функція (їло), а обмеженнями - співвідношення (9), (10).
Задача оптимізації розмірів закуповуваних партій товарів. Припустимо, що деякій організації на плановий період необхідні певні матеріали в об'ємах ![]() . Ці матеріали витрачаються рівномірно в часі і зберігаються на одному складі, місткістю
. Ці матеріали витрачаються рівномірно в часі і зберігаються на одному складі, місткістю ![]() об'ємних одиниць, причому
об'ємних одиниць, причому ![]() , так що одночасно розмістити на складі всі матеріали неможливо і необхідно провести кілька закупок цих матеріалів партіями по
, так що одночасно розмістити на складі всі матеріали неможливо і необхідно провести кілька закупок цих матеріалів партіями по ![]() об'ємних одиниць кожного
об'ємних одиниць кожного ![]() -го товару
-го товару ![]() .
.
Вартість зберігання на складі об'ємної одиниці ![]() -го матеріалу дорівнює
-го матеріалу дорівнює ![]() , так що зберігання
, так що зберігання ![]() одиниць товару протягом часу його використання коштуватиме
одиниць товару протягом часу його використання коштуватиме ![]() . Припустимо, що вартість кожної закупки
. Припустимо, що вартість кожної закупки ![]() -го матеріалу не залежить від розміру партії xj і дорівнює sj. Необхідно визначити оптимальні розміри закуповуваних партій так, щоб мінімізувати загальні витрати на зберігання і закупку матеріалів. Отже, цільова функція задачі
-го матеріалу не залежить від розміру партії xj і дорівнює sj. Необхідно визначити оптимальні розміри закуповуваних партій так, щоб мінімізувати загальні витрати на зберігання і закупку матеріалів. Отже, цільова функція задачі
![]() (11)
(11)
при умові, що сумарний об'єм закуповуваних партій не перевищить місткості складу
![]() (12)
(12)
Очевидно,
![]() (13)
(13)
Задача про режим роботи енергосистеми. В якості приклада задачі опуклого програмування розглянемо простішу задачу про оптимальне ведення режиму роботи енергосистеми.
Розглядається ізольована енергосистема, яка складається з теплоелектростанцій, зв'язаних лініями передач з вузлом, в якому зосереджене навантаження. Ставиться задача розподілу активних потужностей між електростанціями у заданий момент часу. Розподіл здійснюється за критерієм мінімізації сумарних паливних витрат на генерацію активної потужності.
Позначимо через, xj активну потужність, яка генерується на j-й електростанції. Потужності xj лежать у межах, які визначаються технічними умовами:![]() . Крім того, повинно виконуватись умова балансу потужностей, тобто загальна потужність, що генерується, повинна відповідати потужності Р, яка споживається, з урахуванням загальних втрат
. Крім того, повинно виконуватись умова балансу потужностей, тобто загальна потужність, що генерується, повинна відповідати потужності Р, яка споживається, з урахуванням загальних втрат![]() у лініях передач:
у лініях передач:
![]()
Втрати палива на генерацію потужності xj являють собою функцію ![]() , яка опукла на відрізку
, яка опукла на відрізку![]() Таким чином, задача приймає вигляд:
Таким чином, задача приймає вигляд:
![]() (14)
(14)
при умовах
![]() (15)
(15)
![]() (16)
(16)
Побудована модель є типовою задачею опуклого програмування з лінійними обмеженнями. Розв'язок цієї задачі дає вельми грубе наближення до дійсно оптимального режиму роботи енергосистеми. У реальній ситуації не можна вважати все навантаження зосередженим в одному вузлі, а слід розглядати п вузлів. Крім того, втрати в системі, природно не є сталими, а залежать від параметрів ліній передач та величин потужностей, що передаються.
В якості наступного наближення можна розглядати задачу, в якій π є білінійною функцією ![]() , де параметри управління xy означають кількість активної потужності, яка передається з j-й електростанції у i-й вузол.
, де параметри управління xy означають кількість активної потужності, яка передається з j-й електростанції у i-й вузол.
Очевидно, що в цієї нової моделі умови будуть містити нелінійності (π (xy.) в рівнянні балансу).
Задача про розміщення. Ця простіша задача про розміщення є прикладом багатоекстремальної задачі.
Є т можливих пунктів виробництва, причому відома для кожного i-го пункту залежність вартості виробництва fi від об'єму виробництва xi (передбачається, що у вартість виробництва![]() включені капітальні витрати). Дані
включені капітальні витрати). Дані![]() пунктів споживання із заданим об'ємом споживання bj у кожному пункті. Нарешті, задана матриця транспортних витрат (
пунктів споживання із заданим об'ємом споживання bj у кожному пункті. Нарешті, задана матриця транспортних витрат (![]() ) (
) (![]() - вартість перевезення одиниці продукції з i-го пункту виробництва в j-й пункт споживання). Необхідно знайти такі об'єми виробництва
- вартість перевезення одиниці продукції з i-го пункту виробництва в j-й пункт споживання). Необхідно знайти такі об'єми виробництва ![]() , які мінімізують сумарні витрати; інакше кажучи, шукається
, які мінімізують сумарні витрати; інакше кажучи, шукається
![]() (17)
(17)
при умовах
![]() (18)
(18)
![]() (19)
(19)
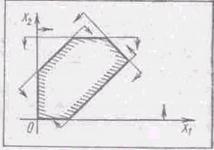
Оскільки собівартість одиниці продукції звичайно спадає при збільшені об'єму виробництва, то функції fi (yi), як правило, монотонно зростають і опуклі вгору. Множина значень xij, що задовольняє обмеження задачі, утворює опуклий многокутник, вершини якого є точками локальних мінімумів функції l(xij) (рис. 1).
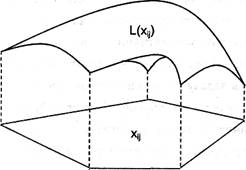
Рис. 1. Звідси й назва подібних задач - багатоекстремальні.
Доцільно зазначити, що за своїм реальним змістом більшість задач математичного програмування є задачами або мінімізації витрат ресурсів на виробництво заданих кількостей продукції, або ж максимізації випуску продукції (прибутку) при заданих обмежених кількостях ресурсів.
2. Дві стандартні форми задач лінійного програмуванняЗагальна форма задачі лінійного програмування (3.1) - (3.6) не придатна для побудови досить простих і ефективних методів розв'язування її, причиною чого е неоднорідність системи умов (3.2) -(3.6). Тому, як правило, задачу зводять до стандартної форми.
В залежності від методів, які застосовуються, розрізняють дві стандартні форми:
основна задача лінійного програмування з обмеженнями-рівностями або перша стандартна форма;
основна задача лінійного програмування з обмеженнями-нерівностями або друга стандартна форма.
Формулювання основної задачі лінійного програмування у першій стандартній формі полягає в наступному: серед усіх невід'ємних розв'язків системи основних обмежень-рівнянь знайти такий, при якому цільова функція набуває найбільшого або найменшого значення:
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
Або у короткому запису
![]() (21а)
(21а)
![]() (22а)
(22а)
Основна задача лінійного програмування може бути також записана у скалярно-векторній, матричній і векторній формах, якщо скористатись позначеннями:
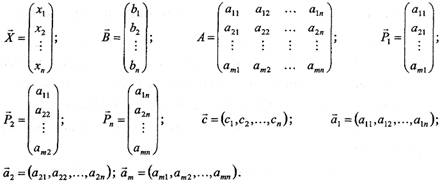
Тут ![]() — вектор-стовпець змінних,
— вектор-стовпець змінних, ![]() — вектор-стовпець вільних членів, А — матриця системи основних обмежень,
— вектор-стовпець вільних членів, А — матриця системи основних обмежень, ![]() - вектор-стовпець матриці А;
- вектор-стовпець матриці А; ![]() — вектор-рядок коефіцієнтів цільової функції,
— вектор-рядок коефіцієнтів цільової функції, ![]() - вектор-рядок матриці А.
- вектор-рядок матриці А.
Скалярно-векторна форма:
![]() (216)
(216)
![]() (22б)
(22б)
![]() (23б)
(23б)
Матрична форма:
![]() (21в)
(21в)
![]() (22в)
(22в)
![]() (23в)
(23в)
Векторна форма:
![]() (21г)
(21г)
![]() (22г)
(22г)
![]() (23г)
(23г)
Лема 1. Будь-яку задачу лінійного програмування у загальній формі можна звести до першої стандартної форми.
Доведення. Покажемо, що будь-яку нерівність, введенням додаткової невідомої можна звести до рівності. Дійсно, нехай деяке обмеження має вигляд
![]()
Перепишемо його таким чином:
![]()
Введемо позначення ![]()
За побудовою ![]() є невід'ємною величиною. Крім того останнє
є невід'ємною величиною. Крім того останнє
співвідношення є рівняння відносно невідомих![]() :
:
![]()
Отже ми прийшли до рівності еквівалентній вихідної нерівності.
За таким самим алгоритмом можна звести до рівності й нерівність з протилежним знаком, але завжди треба нові невідомі додавати до менших частин нерівностей, бо у протилежному випадку вони не будуть невід'ємними величинами.
Наступний крок полягає в зведені до однорідної системи обмежень на знак. Умови недодатності (3.6) легко перетворюються в умови невід'ємності за допомогою заміни відповідних змінних ![]() .
.
Складніше позбутися змінних, на знак яких обмежень не накладено. Цього можна досягти двома способами.
1-й спосіб. Якщо число таких змінних (3.7) менше, ніж число обмежень основної групи і вектори-стовпці коефіцієнтів при них разом з деякими іншими утворюють базисний мінор, то, розв'язавши добуту нами систему обмежень-рівностей відносно згаданих змінних, виключаємо їх як з системи умов, так і з цільової функції, залишаючи без уваги формули, що виражають їх через невід'ємні змінні, підставляючи які у залишені вирази, дістаємо й оптимальні значення змінних (3.7).
Хоч цей спосіб придатний для більшості практичних випадків, однак буває, що умови необхідні для його використання, не виконуються.
Тоді цим способом можна виключити лише частину вільних змінних, а до тих, що залишилися у задачі, застосувати 2-й спосіб.
2-й спосіб. Кожну змінну, на знак якої не накладено обмежень, подають у вигляді різниці двох невід'ємних змінних
![]() (24)
(24)
Визначивши оптимальні значення ![]() та
та ![]() , можемо знайти за (24) і оптимальне значення відповідних
, можемо знайти за (24) і оптимальне значення відповідних ![]()
Приклад 1. Звести до першої стандартної форми таку задачу лінійного програмування:
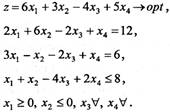
Розв'язання. Введенням однієї додаткової змінної ![]() та заміною
та заміною ![]() зводимо задачу до вигляду
зводимо задачу до вигляду
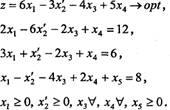
Хоч тут кількість змінних без обмеження на знак і менша від кількості основних обмежень, їх не можна вивести з задачі, оскільки вектори-стовпці їхніх коефіцієнтів пропорційні і не можуть разом входити до базисного мінору. Тому виведемо одну з них, а другу замінимо різницею двох невід'ємних змінних.
Запишемо задачу в таблицю (в нульовий рядок записане рівняння, що відповідає цільової функції:![]()
| № рядка |
|
|
|
|
|
|
| 0 | -6 | 3 | 4 | -5 | 0 | 0 |
| 1 | 2 | -6 | -2 |
| 0 | 12 |
| 2 | 3 | 1 | -2 | 1 | 0 | 6 |
| 3 | 1 | -1 | -4 | 2 | 1 | 8 |
Вибравши ![]() = 1 ключовим елементом, переходимо до нової таблиці.
= 1 ключовим елементом, переходимо до нової таблиці.
| № рядка |
|
|
|
|
|
|
| 0 | 4 | -27 | -6 | 0 | 0 | 60 |
| 1 | 2 | -6 | _2 | 1 | 0 | 12 |
| 2 | 1 | 7 | 0 | 0 | 0 | -6 |
| 3 | -3 | 11 | 0 | 0 | 1 | -16 |
Виписуючи окремо 1-й рядок (виразивши з нього, ![]() )
) ![]() і замінивши
і замінивши ![]() , дістаємо першу стандартну форму задачі
, дістаємо першу стандартну форму задачі
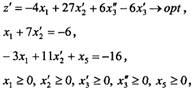
де![]()
Основна задача лінійного програмування у другій стандартній формі полягає в тому, що серед всіх невід'ємних розв'язків системи основних обмежень-нерівностей треба знайти такий, при якому цільова функція буде мати оптимальне значення:
![]() (25)
(25)
![]() (26)
(26)
![]()
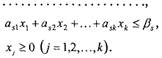 (27)
(27)
Або у короткому запису
![]() (25а)
(25а)
![]() (26а)
(26а)
Скалярно-векторна форма:
![]() (25б)
(25б)
![]() (26б)
(26б)
![]() (27б)
(27б)
Матрична форма:
![]() (25в)
(25в)
![]() (26в)
(26в)
![]() (27в)
(27в)
Векторна форма:
![]() (25г)
(25г)
![]() (26г)
(26г)
![]() (27г)
(27г)
Лема 2. Перша стандартна форма основної задачі лінійного програмування завжди може бути зведена до другої стандартної форми.
Доведення. Припустимо, що невідомі ![]() є вільними;
є вільними;
![]() - базисними; ранг матриці системи обмежень (22) дорівнює
- базисними; ранг матриці системи обмежень (22) дорівнює![]()
Розв'яжемо систему рівнянь (22) відносно базисних невідомих і нехай розв'язок має вигляд
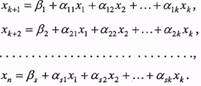 (28)
(28)
Всі невідомі невід'ємні, тому
![]()
Враховуючи це, поставимо у відповідність отриманому розв'язку (28) еквівалентну систему нерівностей:
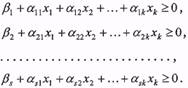
Введемо позначення![]() і помноживши всі нерівності на -1 отримуємо систему обмежень:
і помноживши всі нерівності на -1 отримуємо систему обмежень:
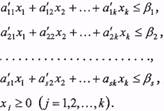
Очевидно, що остання система обмежень збігається з (26) і рівносильна системі обмежень (3-9) У тому розумінні, що будь-якому розв'язку ![]() системи нерівностей відповідає певний розв'язок
системи нерівностей відповідає певний розв'язок ![]() системи рівнянь (22) Для завершення доведення леми підставимо у цільову функцію (21) замість базисних невідомих
системи рівнянь (22) Для завершення доведення леми підставимо у цільову функцію (21) замість базисних невідомих ![]() їхні вирази (28). Якщо згрупувати подібні члени, то цільова функція набуде вигляду (25). Приклад 2. Звести до другої стандартної форми задачу
їхні вирази (28). Якщо згрупувати подібні члени, то цільова функція набуде вигляду (25). Приклад 2. Звести до другої стандартної форми задачу
![]()
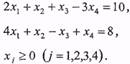
Розв'язання. Виписуємо матрицю системи обмежень
![]()
і шукаємо ранг матриці. Базисним буде мінор
![]()
Отже, ранг ![]() . Базисні невідомі:
. Базисні невідомі: ![]() ; вільні невідомі:
; вільні невідомі: ![]()
Розв'язуємо систему відносно базисних невідомих:
![]()
Так як![]() , то
, то
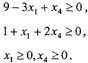
Запишемо цільову функцію z через вільні невідомі
![]()
Отже, задача, рівносильна вихідній, має вигляд:
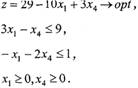
Із лем 1, 2 випливає така теорема.
Теорема 1. Основна задача лінійного програмування у першій стандартній формі і основна задача лінійного програмування у другій стандартній формі еквівалентні між собою
3. Економічна модель задачіФірма спеціалізується на виготовленні та реалізації електроплит і морозильних камер. Припустимо, що збут продукції необмежений, проте обсяги ресурсів (праці та основних матеріалів) обмежені. Завдання полягає у визначенні такого плану виробництва продукції на місяць, за якого виручка була б найбільшою.
Норми використання ресурсів та їх загальний запас, а також ціни одиниці кожного виду продукції наведені в табл. 1.
Таблиця 1 Інформація, необхідна для складання виробничої програми
| Вид продукції | Норми витрат на одиницю продукції | Ціна одиниці продукції, ум. од. | ||
| робочого часу, люд.-год. | листового заліза, м2 | скла, м2 | ||
| Морозильна камера | 9,2 | 3 | — | 300 |
| Електрична плита | 4 | 6 | 2 | 200 |
| Загальний запас ресурсу на місяць | 520 | 240 | 40 | — |
Побудуємо економіко-математичну модель даної задачі.
Позначимо через![]() кількість вироблених морозильних камер, а через,
кількість вироблених морозильних камер, а через, ![]() — електроплит. Виразимо математично умови, що обмежують використання ресурсів.
— електроплит. Виразимо математично умови, що обмежують використання ресурсів.
Виходячи з нормативів використання кожного з ресурсів на одиницю продукції, що наведені в табл. 1, запишемо сумарні витрати робочого часу:
![]() .
.
За умовою задачі ця величина
не може перевищувати загальний запас даного ресурсу, тобто 520 люд.-год. Ця вимога описується такою нерівністю:
![]()
Аналогічно запишемо умови щодо використання листового заліза та скла:
![]()
Необхідно серед множини всіх можливих значень![]() та
та![]() знайти такі, за яких сума виручки максимальна, тобто: max
знайти такі, за яких сума виручки максимальна, тобто: max![]()
Отже, умови задачі, описані в прикладі 1.1, можна подати такою економіко-математичною моделлю:
![]() 5
5
за умов:
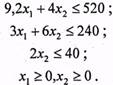
Остання умова фіксує неможливість набуття змінними від'ємних значень, тому що кількість виробленої продукції не може бути від'ємною. Розв'язавши задачу відповідним методом математичного програмування, дістаємо такий розв'язок: для максимальної виручки від реалізації продукції необхідно виготовляти морозильних камер — 50 штук, електроплит — 15 (![]() =50,
=50,![]() =15).
=15).
Перевіримо виконання умов задачі:
9,2-50 + 4·15 = 520;
3-50 + 6·15 = 240;
2·15 = 30<40.
Всі умови задачі виконуються, до того ж оптимальний план дає змогу повністю використати два види ресурсів з мінімальним надлишком третього.
Виручка становитиме: F = 300-50 + 200-15 = 18000 ум. од.
Отриманий оптимальний план у порівнянні з першим варіантом виробничої програми уможливлює збільшення виручки на
18000-16 800 = 1200 ум. од., тобто на![]() 100% = 7,1%
100% = 7,1%
Математична модель стандартної задачі – це її спрощений образ, поданий у вигляді сукупності математичних співвідношень (нерівностей). Загальна задача лінійного програмування (ЛП) подається у вигляді:
знайти максимум (мінімум) функції
![]() (29)
(29)
або![]()
за умов
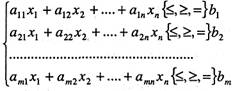 (30)
(30)
![]() (31)
(31)
Отже, потрібно знайти значення змінних![]() , які задовольняють умови (30) і (31), тоді як цільова функція набуває екстремального (максимального чи мінімального) значення.
, які задовольняють умови (30) і (31), тоді як цільова функція набуває екстремального (максимального чи мінімального) значення.
Задачу (29)—(2.3) легко звести до канонічної форми, тобто до такого вигляду, коли в системі обмежень (30) всі ![]() (і =1,2, ...... n) невід'ємні, а всі обмеження є рівностями.
(і =1,2, ...... n) невід'ємні, а всі обмеження є рівностями.
Якщо якесь![]() від'ємне, то, помноживши
від'ємне, то, помноживши ![]() -те обмеження на (—1), дістанемо у правій частині відповідної рівності додатне значення. Коли i-те обмеження має вигляд нерівності ,
-те обмеження на (—1), дістанемо у правій частині відповідної рівності додатне значення. Коли i-те обмеження має вигляд нерівності ,![]()
![]() , то останню завжди можна звести до рівності, увівши допоміжну змінну
, то останню завжди можна звести до рівності, увівши допоміжну змінну
![]()
Аналогічно обмеження виду ![]() зводимо до рівності, віднімаючи від лівої частини допоміжну змінну
зводимо до рівності, віднімаючи від лівої частини допоміжну змінну ![]() ,тобто І
,тобто І![]()
Приклад 2.1. Записати в канонічній формі таку задачу ЛП:
![]()
за умов
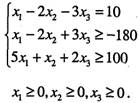
Розв'язування. Помножимо другу нерівність на (-1) і введемо відповідно допоміжні змінні![]() і
і![]() для другого та третього обмеження:
для другого та третього обмеження:
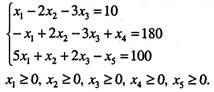
Неважко переконатися, що допоміжні змінні, у цьому разі![]() і
і ![]() , є невід'ємними, причому їх уведення не змінює цільової функції.
, є невід'ємними, причому їх уведення не змінює цільової функції.
Отже, будь-яку задачу ЛП можна записати в такій канонічній формі:
знайти максимум функції![]() (32)
(32)
за умов
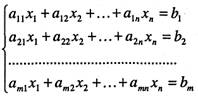 (33)
(33)
![]() (34)
(34)
Задачу (32)—(34) можна розв'язувати на мінімум, якщо цільову функцію помножити на (-1), тобто
![]()
Геометрична інтерпретація аналітичних задач дає можливість наочно представити їх структуру, що сприяє засвоєнню їхніх основних властивостей та відкриває шляхи виявлення і дослідження інших, більш складних властивостей цих задач. У найпростіших випадках геометричне подання дає змогу знайти розв'язок задачі, однак навіть у тривимірному просторі геометричне розв'язування ускладнюється і створює ряд труднощів у побудові відповідних геометричних фігур, а в просторах вимірності, більшої за три, таке розв'язування і зовсім неможливе.
Можливі різноманітні форми і способи геометричного представлення задач лінійного програмування. Доцільність вибору кожного способу зумовлюється метою, якої хочуть досягти даною геометричною інтерпретацією та особливостями структури самої задачі, в тому числі й формою її представлення.
Для геометричної інтерпретації візьмемо основну задачу лінійного програмування у другій стандартній формі. Для наочності розглянемо найпростіший випадок, коли в системі обмежень (26) і цільовій функції (25) є лише дві змінних![]() ,
,![]()
Розглянемо розв'язування нерівностей.
Лема 3. Множина розв'язків нерівності з двома змінними
![]()
є однією з двох півплощин, на які вся площина ділиться прямою ![]() , включаючи й цю пряму, а інша півплощина з тією ж прямою є множиною розв'язків нерівності
, включаючи й цю пряму, а інша півплощина з тією ж прямою є множиною розв'язків нерівності
![]()
Доведення. Гранична пряма ![]() перпендикулярна до вектора нормалі .
перпендикулярна до вектора нормалі .![]() (рис 3.1). Вектор нормалі (його ще називають напрямним вектором ) є градієнтом лінійної функції
(рис 3.1). Вектор нормалі (його ще називають напрямним вектором ) є градієнтом лінійної функції ![]() і показує напрям зростання її значень
і показує напрям зростання її значень ![]() — одиничні вектори вздовж осей
— одиничні вектори вздовж осей![]() і
і![]() відповідно; таким чином,
відповідно; таким чином, ![]() . Справді, нехай
. Справді, нехай ![]() ,
,![]() . Візьмемо на прямій, яка визначається вектором
. Візьмемо на прямій, яка визначається вектором ![]() точку
точку ![]() , причому нехай
, причому нехай ![]() , тобто точка
, тобто точка ![]() лежить далі від початку координат, ніж точка
лежить далі від початку координат, ніж точка![]() . Очевидно також, що
. Очевидно також, що ![]() . У точці
. У точці ![]() числове значення
числове значення ![]() лінійної функції
лінійної функції ![]() дорівнює
дорівнює ![]() . Аналогічно в точці
. Аналогічно в точці ![]() значення
значення ![]() . Ураховуючи, що
. Ураховуючи, що ![]() , дістанемо
, дістанемо ![]()
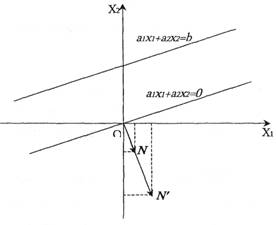
Рис. 1.
Аналогічно можна пересвідчитись, що напрям зменшення значень лінійної функції ![]() збігається з напрямним вектором
збігається з напрямним вектором ![]()
Прямі лінії на площині![]() , які паралельні прямій, що визначається рівнянням
, які паралельні прямій, що визначається рівнянням![]() називають лініями рівнів лінійної функції
називають лініями рівнів лінійної функції ![]() . Користуючись поняттям напрямного вектора
. Користуючись поняттям напрямного вектора ![]() , можемо визначити розміщення півплощин
, можемо визначити розміщення півплощин![]() і
і ![]() на координатній площині
на координатній площині ![]() . Півплощина
. Півплощина ![]() розміщена по той бік прямої
розміщена по той бік прямої![]() , куди показує напрямний вектор -
, куди показує напрямний вектор -![]() . Аналогічно вектор
. Аналогічно вектор ![]() показує, де розміщена півплощина
показує, де розміщена півплощина ![]() відносно прямої
відносно прямої ![]() побудуємо напрямний вектор N = (3,-2). Напрямний вектор міститься у шуканій півплощині, яка виділена штриховими лініями (рис 3.2).
побудуємо напрямний вектор N = (3,-2). Напрямний вектор міститься у шуканій півплощині, яка виділена штриховими лініями (рис 3.2).
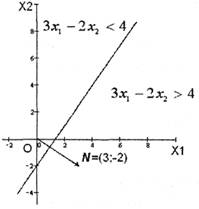
Рис. 3.2
Якщо врахувати, що множина точок, що задовольняє рівняння
![]() 29.)
29.)
при п = 3, є півплощина, а при п > 3 - гіперплощина в n-вимірному просторі, то лему 3 можна поширити на випадок трьох і більше змінних.
Теорема 2. Множиною всіх розв'язків лінійної нерівності з п змінними
![]()
є одним з півпросторів, на які весь простір розділяється площиною або гіперплощиною (29), включаючи й саму площину (гіперплощину).
Розглянемо множину розв'язків систем нерівностей.
Теорема 3. Множиною розв'язків сумісної системи т лінійних нерівностей з двома змінними
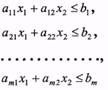
є опуклим многокутником.
Доведення. Кожна з нерівностей у відповідності з лемою 3 визначає одну з півплощин, які є опуклими множинами точок. Множиною розв'язків сумісної системи лінійних нерівностей є множина точок, які належать півплощинам-розв'язкам усіх нерівностей, тобто належать їх перетину. Згідно теореми 2 про перетин опуклих множин ця множина є опуклою і містить скінчене число кутових точок, тобто є опуклим многокутником.
Теорема 4. Множина розв'язків сумісної системи т лінійних нерівностей з п змінними є опуклим многогранником в n-вимірному просторі.
Теорема 5. Множиною всіх допустимих розв'язків сумісної системи т лінійних рівнянь з п змінними (![]() ) є опуклим многогранником в n-вимірному просторі.
) є опуклим многогранником в n-вимірному просторі.
Теорема 6. Оптимальне значення задачі лінійного програмування досягається у вершині многогранника розв'язків системи обмежень.
Результати цього підрозділу дають змогу так інтерпретувати задачі лінійного програмування:
У многограннику (многокутнику у випадку двох змінних) розв'язків системи обмежень задачі лінійного програмування знайти таку вершину, де цільова функція набуває оптимального (найбільшого або найменшого) значення.
Нехай фермер прийняв рішення вирощувати озиму пшеницю і цукрові буряки на площі 20 га, відвівши під цукрові буряки не менше як 5 га. Техніко-економічні показники вирощування цих культур маємо у табл. 2:
Таблиця 2 Показники вирощування сільськогосподарських культур
| Показник (із розрахунку на 1 га) | Озима пшениця | Цукрові буряки | Наявний ресурс |
| Затрати праці, людино-днів | 5 | 25 | 270 |
| Затрати праці механізаторів, людино-днів | 2 | 8 | 80 |
| Урожайність, тонн | 3,5 | 40 | — |
| Прибуток, тис. грн. | 0,7 | 1 | — |
Критерієм оптимальності є максимізація прибутку.
Запишемо економіко-математичну модель структури виробництва озимої пшениці та цукрових буряків, ввівши такі позначення:
x1 — шукана площа посіву озимої пшениці, га;
x2— шукана площа посіву цукрових буряків, га.
Задача лінійного програмування має такий вигляд:
![]() (38)
(38)
за умов:
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
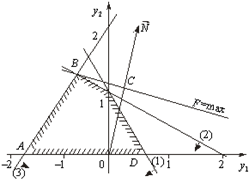
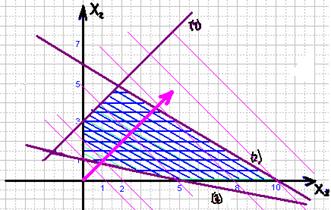
Геометричну інтерпретацію задачі зображено на рис. 2.2.
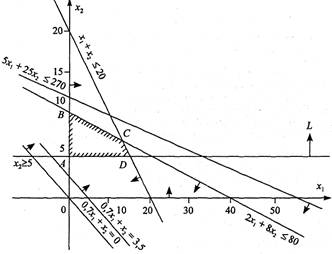
Рис. 2.2. Область допустимих розв'язків задачі
Область допустимих розв'язків цієї задачі дістаємо так. Кожне обмеження, наприклад ![]() задає півплощину з граничною прямою
задає півплощину з граничною прямою ![]() . Будуємо її і визначаємо півплощину, яка описується нерівністю
. Будуємо її і визначаємо півплощину, яка описується нерівністю ![]() .З цією метою в нерівність
.З цією метою в нерівність ![]() підставляємо координати характерної точки, скажімо,
підставляємо координати характерної точки, скажімо,![]() і
і![]() . Переконуємося, що ця точка належить півплощині
. Переконуємося, що ця точка належить півплощині ![]() . Цей факт на рис. 2.2 ілюструємо відповідною напрямленою стрілкою. Аналогічно будуємо півплощини, які відповідають нерівностям (39)—(43). У результаті перетину цих півплощин утворюється область допустимих розв'язків задачі (на рис. 2.2 — чотирикутник ABCD). Цільова функція Z = 0,7x1+х2 являє собою сім'ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z=0, то маємо Z = 0,7x1+х2=0. Ця пряма проходить через початок системи координат. Коли Z= 3,5, то маємо пряму 0,7x1+х2=3,5.
. Цей факт на рис. 2.2 ілюструємо відповідною напрямленою стрілкою. Аналогічно будуємо півплощини, які відповідають нерівностям (39)—(43). У результаті перетину цих півплощин утворюється область допустимих розв'язків задачі (на рис. 2.2 — чотирикутник ABCD). Цільова функція Z = 0,7x1+х2 являє собою сім'ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z=0, то маємо Z = 0,7x1+х2=0. Ця пряма проходить через початок системи координат. Коли Z= 3,5, то маємо пряму 0,7x1+х2=3,5.
Графічний метод для визначення оптимального плану задачі лінійного програмування доцільно застосовувати лише для задач із двома змінними. За більшої кількості змінних вдаються до загального методу розв'язування задач лінійного програмування — так званого симплекс-методу. Процес розв'язування задачі симплекс-методом має ітераційний характер: обчислювальні процедури (ітерації) одного й того самого типу повторюються у певній послідовності доти, доки не буде отримано оптимальний план задачі або з’ясовано, що його не існує.
Отже, симплекс-метод — це поетапна обчислювальна процедура, в основу якої покладено принцип послідовного поліпшення значень цільової функції переходом від одного опорного плану задачі лінійного програмування до іншого.
Алгоритм розв'язування задачі лінійного програмування симплекс-методом складається з п'яти етапів:
1. Визначення початкового опорного плану задачі лінійного програмування.
2. Побудова симплексної таблиці.
3. Перевірка опорного плану на оптимальність за допомогою оцінок ![]() . Якщо всі оцінки задовольняють умову оптимальності, то визначений опорний план є оптимальним планом задачі. Якщо хоча б одна з оцінок
. Якщо всі оцінки задовольняють умову оптимальності, то визначений опорний план є оптимальним планом задачі. Якщо хоча б одна з оцінок ![]() не задовольняє умову оптимальності, то переходять до нового опорного плану або встановлюють, що оптимального плану задачі не існує.
не задовольняє умову оптимальності, то переходять до нового опорного плану або встановлюють, що оптимального плану задачі не існує.
Похожие работы
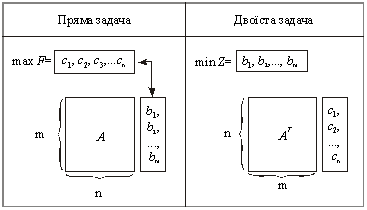
... виокремлюють певні підкласи. Наприклад, ігри двох осіб із нульовою сумою. Наведену класифікацію використано для структурування курсу «Математичне програмування». 2. Економічна інтерпретація прямої та двоїстої задач лінійного програмування Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари таких задач розглянемо ...
... розвиток як математична теорія лінійного і нелінійного програмування, так і додаток її методів до дослідження різних економічних проблем. У 1949 р. американським математиком Дж. Данцигом (GB Dantzig) був опублікований симплекс-метод - основний метод рішення задач лінійного програмування. Термін «лінійне програмування» вперше з'явився в 1951 р. в роботах Дж. Данцига і Т. Купманса. При всьому ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
ача має назву задачі безумовного програмування. У якості прикладів економічних проблем, які доцільно розв’язувати. використовуючи методи та моделі математичного програмування, розглянемо такі: Приклад 1. Задача про планування випуску продукції малого підприємства. Планується виробляти жіночі та чоловічі костюми. На жіночій костюм потрібно 1 м. шерсті, 2 м. шовку та 1 людино-тиждень працевитрат. ...
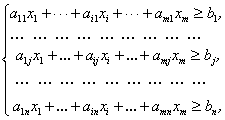
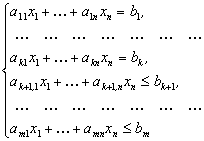
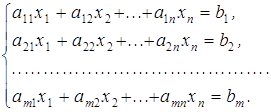
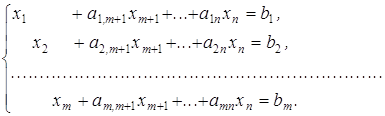
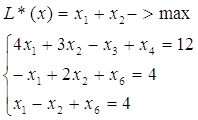

0 комментариев