Навигация
Контрольний приклад та результат машинного експерименту
2.3 Контрольний приклад та результат машинного експерименту
Найбільш відповідальною, найбільш трудомісткою і з найбільшими витратами часу є випробовування (створення програм та усунення помилок. Не можна бути впевненим, що програма працює правильно коли вона виводить якісь результати. Найчастіше ці результати перші) бувають помилковими. Це означає, що багато помилок. Тому для перевірки правильності програми необхідно розробити тестові дані з наперед визначеними (обчисленими) результатами. Тестові дані повинні бути розроблені так, щоб перевірити всі оператори програми без виключення.
Для перевірки на правильність даної програми розроблені наступні тести:
Тест 1.
Система з трьома невідомими

Результати: ![]()
Порівнявши результати обчислені вручну до тестових даних і результати обчислені за допомогою програми Kursova.pas, фкі подані у додатку бачимо що все співпадає, тому можна стверджувати, що програма дає правильні результати і саме не містить помилок. Однак остаточним висновок про правильність програми можна зробити тільки після тривалої експлуатації.
Висновок
Розв’язування математичних задач за допомогою персональних комп’ютерів має велике значення, оскільки кожен розв’язок є оперативним та точним. Обчислюючи математичну задачу за допомогою сучасного комп’ютера, зрозуміло, що ймовірність помилкового введення даних в пам’ять ПК є набагато більшою чим ймовірність помилкового обчислення комп’ютером, чим тут практично можна знехтувати. Тоді що вже можна говорити про порівняня ручного обчислення і машинного. Тому надзвичайно важливо самостійно складати програми для виникаючих задач, які потрібно часто рішати. Звичайно головним в написанні програми є правильність її складання, оскільки правильність результатів обчислення найперш залежить від правильності програми.
В даній курсовій роботі складено програму по обчисленню різних систем рівнянь з квадратною матрицею. Дану програму розроблено в середовищі Turbo Pascal. Її налагоджено з використанням різноманітних тестових даних. Прикладом для перевірки роботоздатності програми було розроблено вручну тест. Результати обчислення вручну та за допомогою комп’ютера повністю співпали. Тому можна вважати цей програмний продукт готовим для практичного застосування.
Список використаної літератури
Turbo pascal(учебник) / С.А. Немнюгин – СПБ: Издательство “Питер”, 2000.
М.Я. Ляшенко, М.С. Головань. Чисельні методи. К.:”Либідь”, 1996 – 285 с.
Математика для техникумов – Алгебра и начала анализа.
Додаток 1
(***********************************************************)
(* програма по розвязуванню *)
(* систем лiнiйних рiвнянь *)
(* методом Жордана-Гауса,написана до курсового проекту. *)
(* Програму склав Добромильський Iван *)
(************************************************************)
{001} program metod_Zhordana_Hausa;
{002} uses crt;
{003} const m!;
{004} type m_1=array[1..m,1..m] of real;
{005} m_2=array[1..m] of real;
{006} m_3=array[1..m] of integer;
{007} label m1;
{008} var A,B:m_1; X:m_2; C,D,E:m_3;
{009} R:real;
{010} i,j,k,t,l,z,h,n,p:integer;
{011} s:char;
(* Процедура виводу рамки *)
{012} procedure ramka(x1,y1,x2,y2:integer);
{013} begin
{014} gotoxy(x1,y1);write('Й');
{015} for i:=1 to x2-x1-1 do write('Н');
{016} write('»');
{017} for i:=1 to y2-y1-1 do begin
{018} gotoxy(x2,y1+i);write('є');
{019} gotoxy(x1,y1+i);write('є');
{020} end;
{021} gotoxy(x1,y2);write('И');
{022} for i:=1 to x2-x1-1 do write('Н');
{023} write('ј');
{024} gotoxy(x1+3,y1);write('[ю]');
{025} end;
(* Процедура опису вiкна *)
{026} procedure windo(x1,y1,x2,y2:integer;Nazva:string);
{027} begin
{028} TextColor(15);
{029} TextBackGround(1);
{030} Window(x1,y1,x2,y2);
{031} clrscr;
{032} ramka(2,1,x2-x1,y2-y1+1);
{033} l:=x2-x1+1-length(nazva);
{034} gotoxy((l div 2)+3,1);write(Nazva);
{035} end;
(* Процедура виводу загального опису *)
{036} procedure vikno;
{037} begin
{038} TextBackGround(15);TextColor(1);
{039} for i:=1 to 80 do
{040} for j:=1 to 25 do begin
{041} gotoxy(i,j);write(' ');
{042} end;
{043} windo(50,2,75,7,' Меню ');
{044} gotoxy(3,2);write('F1-Ввiд розмiрностi');
{045} gotoxy(3,3);write('F2-Ввiд даних');
{046} gotoxy(3,4);write('F3-Вивiд результатiв');
{047} gotoxy(3,5);write('ESC-Вихiд');
{048} windo(50,10,78,16,' Про автора ');
{049} gotoxy(3,2);write('Програма курсово» роботи.');
{050} gotoxy(3,3);write('Складена студентом групи');
{051} gotoxy(3,4);write('39-П Добромильським I.');
{052} gotoxy(3,5);write('Дата складення програми');
{053} gotoxy(3,6);write('травень 2003р');
{054} end;
(* Процедура виводу вiкна *)
{055} procedure wind(x1,y1,x2,y2:integer;Nazva:string);
{056} begin
{057} vikno;
{058} windo(x1,y1,x2,y2,nazva);
{059} end;
(* Пороцедуга вводу розмiрностi квадратно» матрицi *)
{060} procedure vvidn;
{061} begin
{062} wind(2,2,47,5,'=Ввiд розмiрностi квадратно» матрицi');
{063} gotoxy(3,2); write('n=');
{064} readln(n);
{065} if n>=m then begin
{066} wind(2,2,40,6,'Повiдомлeння');
{067} gotoxy(4,3);writeln('Розмiрнiсть повинна не бiльша ',m-1,'');
{068} S:= readkey;
{069} end;
{070} end;
(* Процедура вводу елементiв *)
{071} procedure vvid;
{072} label m8;
{073} begin
{074} k:=n;
{075} if k>4 then
{076} k:=4;
{077} t:=1;
{078} z:=1;
{079} h:=1;
{080} m8:wind(2,2,35,k*k+k+3,'Ввiд елементiв');
{081} for i:=z to n do
{082} for j:=h to n+1 do begin
{082} gotoxy(3,t+1);
{084} if j<=n then write ('Елемент a[',i,j,']=')
{085} else write ('Вiльний елемент a[',i,j,']=');
{086} readln(A[i,j]);
{087} if t>19 then begin
{088} t:=1;
{089} z:=i;
{090} if j<(n+1) then h:=j+1
{091} else begin
{092} z:=i+1;
{193} h:=1;
{194} end;
{195} clrscr;
{196} goto m8;
{197} end;
{198} if t<_ then begin
{199} t:=t+1;
{100} z:=1;
{101} h:=1;
{102} end;
{103} end;
{104} end;
(* Процедура обчислення невiдомих *)
{105} procedure obchuslennja;
{106} label m2,m3,m4,m5,m6,m7;
{107} begin
{108} j:=n+1;
{109} for i:=1 to n do
{110} A[i,j]:=-A[i,j];
{111} t:=0;
{112} l:=n;
{113} for i:=1 to l+1 do
{114} E[i]:=0;
{115} for p:=1 to n do begin
{116} i:=0;
{117} m2:if i=n then goto m6
{118} else i:=i+1;
{119} j:=0;
{120} m3:if j=t then goto m4
{121} else j:=j+1;
{122} if i=C[j] then goto m2
{123} else goto m3;
{124} m4:j:=0;
{125} m5:j:=j+1;
{126} if(i=n)and(j=l)and(A[i,j]=0) then goto m6;
{127} if (j=l)and(A[i,j]=0) then goto m2;
{128} if A[i,j]=0 then goto m5
{129} else begin
{130} k:=i;
{131} h:=j;
{132} end;
{133} R:=A[k,h];
{134} for i:=1 to n do
{135} for j:=1 to l+1 do begin
{136} if(i<>k)and(j<>h) then
{137} B[i,j]:=R*A[i,j]-A[i,h]*A[k,j];
{138} if (i=k)and(j<>h) then
{139} B[i,j]:=-A[i,j];
{140} End;
{141} for i:=1 to n do
{142} for j:=1 to l do begin
{143} if j<h then
{144} A[i,j]:=B[i,j]/R;
{145} if j>=h then begin
{146} z:=j+1;
{147} A[i,j]:=B[i,z]/R;
{148} end;
{149} end;
{150} t:=t+1;
{151} C[t]:=k;
{152} D[k]:=E[h]+h;
{153} for i:=1 to l+1 do begin
{154} if i>h then begin
{155} z:=i-1;
{156} E[z]:=E[i]+1;
{157} end;
{158} end;
{159} l:=l-1;
{160} END;
{161} z:=1;
{162} for i:=1 to n do begin
{163} j:=D[i];
{164} X[i]:=A[j,z];
{165} end;
{166} t:=0;
{167} wind(2,2,45,n+3,'Результати');
{168} for i:=1 to n do begin
{169} gotoxy(5,i+1);writeln('x[',i,']=',X[i]:8:3);
{170} t:=t+1;
{171} end;
{172} goto m7;
{173} m6:wind(2,2,45,6,'Повiдомлення');
{174} gotoxy(10,3); write('Система не ма№ розвязкiв');
{175} m7: s:=readkey;
{176} end;
(* Головний блок програми *)
{177} BEGIN
{178} m1:vikno;
{179} s:=readkey;
{180} case s of
{181} #59:vvidn;
{182} #60:vvid;
{183} #61: obchuslennja;
{184} #27:halt;
{185} end;
{186} goto m1;
{187} END.
Додаток 4
Екранна форма виводу результатів обчислення
|
|
| x[1]= 4.000 x[2]= -1.000 x[3]= 2.000 | F1-Ввiд розмiрностi F2-Ввiд даних F3-Вивiд результатiв ESC-Вихiд | |||
| ||||
| Програма курсової роботи. Складена студентом групи 39-П Добромильським I. Дата складення програми травень 2003р |
Похожие работы
... , ary2s Типы данных для переменных, в которых хранятся значения коэффициентов системы Unit2 Gauss1 Процедура для решения системы линейных уравнений методом Гаусса Unit2 Gaussj Процедура для решения системы линейных уравнений методом Жордана-Гаусса Unit2 i,j,l Счетчики Unit1 prover Промежуточная переменная типа String, используется для проверки наличия букв среди коэффициентов ...
... на місце вектора А3 вводимо вектор А1 та знову робимо перерахунок системи в таблиці 2 за методом Жордана-Гаусса, взявши за провідний елемент а11 = 1,5. Таблиця 3. Третій крок симплекс-методу i Б Сб сk 3 2 0 0 A0 A1 A2 A3 A4 1 A1 3 1 1 0 0,666667 -0,33333 2 A2 2 2 0 1 -0,33333 0,66667 Dk 7 0 0 1,33333 0,33333 Таким чином ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
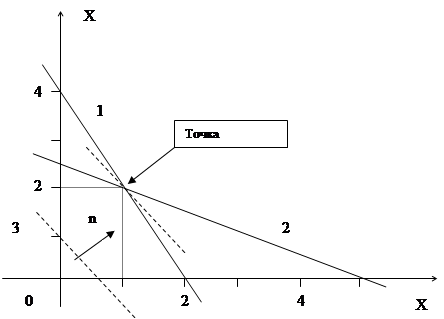
... на t3 часов. Прибыль от реализации единицы готового изделия А составляет a рублей, а изделия В - b рублей. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу простым симплекс-методом. Дать геометрическое истолкование задачи, используя для этого её формулировку с ограничениями-неравенствами. а1 = 1 b1 = 5 t1 = 10 a = 2 а2 = 3 b2 = 2 t2 ...

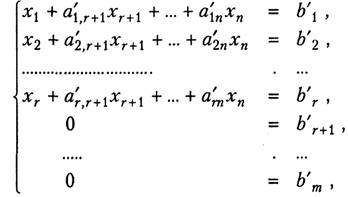

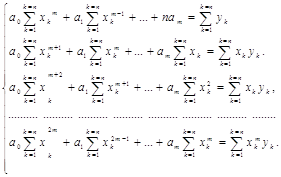
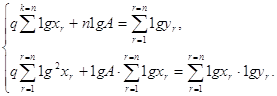
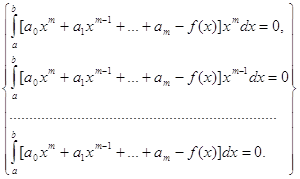
0 комментариев