Навигация
Змістовний опис заданої системи обробки інформації
1 Змістовний опис заданої системи обробки інформації
Імітаційне моделювання – моделювання, де система замінюється на її імітатор, і з ним проводяться досліди з метою отримання інформації про систему. Математичне моделювання полягає в заміні системи її математичною моделлю і проведенні експериментів з нею, а не з самою системою. В основу імітаційного моделювання покладена методологія системного аналізу, тому для рішення нашої задачі використаємо імітаційне моделювання.
До системи обробки інформації, що представлена ЕОМ, надходять дані від датчиків та вимірювальних пристроїв. Цей процес нам потрібно змоделювати. Моделювання буде виконано спрощено тому, що використані будуть тільки задані основні характеристики, такі, як швидкість надходження повідомлень від датчиків, ємність черги, час обробки повідомлення процесором. І знехтуємо всіма іншими параметрами, що можуть вплинути на задану систему. До таких параметрів можна віднести перешкоди на лінії, коллізія, затримки при передачі та багато інших.
З постановки задачі, що визначена у вступі, маємо наступні границі та обмеження:
- границі моделювання обмежені кількістю повідомлень(450 повідомлень);
- повідомлення надходить через кожні 5±2 секунд;
- для обробки повідомлення ЕОМ потрібно 7±3 секунд;
- якщо ЕОМ не обробила повідомлення протягом 13 секунд, то воно втрачається;
Для того щоб мати змогу швидко порівняти варіанти нашої системи, що працює в системі управління технологічним процесом, нам необхідно виконати моделювання із можливістю швидко змінювати основні параметри.
Критерій якості допоможе нам з'ясувати адекватність роботи нашої імітаційної моделі. Критерієм якості обираємо коефіцієнт завантаження ЕОМ, що обчислюється як відношення часу, що мав бути витрачений на обробку повідомлень, до всього фактичного часу. Так ми зможемо оцінити кількість втрачених повідомлень і зробити висновки про роботу нашої системи.
2 Складання концептуальної моделі ЕОМ, яка працює в системі управління технологічним процесом
Як видно з опису системи, вона складається із двох основних елементів: датчиків та ЕОМ. Від датчиків до ЕОМ надходять повідомлення для обробки через деякий випадковий проміжок часу. Даний процес надходження повідомлень є дуже схожим на процес в СМО, тому в якості концептуальної моделі можна використати саме СМО. Система масового обслуговування – це будь-яка система, призначена для обслуговування повідомлень, що надходять у випадкові моменти часу. В нашому випадку датчики та вимірювальні пристрої надсилають дані з деякиою випадковою інтенсивністю до системи обробки (рисунок 1).
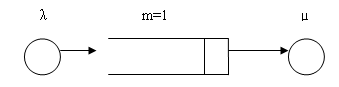

Рисунок 1 – Схема функціонування системи обробки інформації від датчиків
Після того як повідомлення попало до ЕОМ, то воно займає певний час в заданому інтервалі. Якщо при надходжені повідомлення обчислювальний пристрій зайнятий, то повідомлення встає до буферної пам’яті, якщо пам’ять вільна, або втрачається, тобто наша СМО є одноканальною та з обмеженою чергою. Далі коли ЕОМ звільняється, то повідомлення з буферної пам’яті переміщується до ЕОМ для обчислення, та пам’ять , що для черги звільняється. Обсяг буферної пам’яті дозволяє зберігати в ній лище 1 повідомлення. Технологічний процес має такий вигляд, що обчислювальний пристрій обробляє лише ті повідомлення, які чекають в буферній пам’яті не більше 13 секунд, а інші повідомлення теж вважаються втраченими. Змодулюємо систему, де будуть надходити для обробки 450 повідомлень. Також необхідно перевірити адекватність створеної моделі. Для цього змінимо розподіл надходження повідомлень у часі з рівномірного на експонентційний. Таким чином, отримаємо таку модель СМО, параметри якої можна розрахувати з використанням математичної моделі. Порівнюючи обчислені значення з даними, які буде отримано шляхом моделювання, можно буде зробити висновки про адекватність імітаційної моделі, створеної в данній роботі.
3 Формальний опис процесу надходження повідомлень до ЕОМ
Повідомлення надходять до ЕОМ з рівномірним розподілом. Розглянемо рівномірний закон розподілу випадкової величини: Випадкова величина ![]() називаеться рівномірно розподіленою на відрізку [а,b](а і b – це параметри розподілення), якщо її функція щільності має наступний вид
називаеться рівномірно розподіленою на відрізку [а,b](а і b – це параметри розподілення), якщо її функція щільності має наступний вид

Графік функції щільності рівномірного розподілу на відрізку [a,b] випадкової величини приведена на рисунку 2.
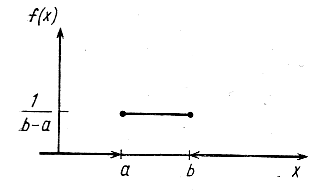
Рис. 2. Функція щільності f(x) рівномірно розподіленої на відрізку [a,b] випадкової величини
Для перевірки адекватності розробленої моделі треба використати модель, в якій можно разрахувати параметри математично. У даному випадку розглядається СМО – найпростіша з чергою, в якій заявки підлягаюсь експоненційному закону розподілу. Розглянемо експоненційний закон розподілу випадкової величини: Неперервна випадкова величина ![]() називається розподіленою за експоненційним законом з параметром Q, якщо функція щільності f(x) випадкової величини
називається розподіленою за експоненційним законом з параметром Q, якщо функція щільності f(x) випадкової величини ![]() має наступний вигляд
має наступний вигляд
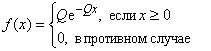
де Q>0.
Графік функції щільності експоненційно розподіленої випадкової величини представлено на рис. 3.
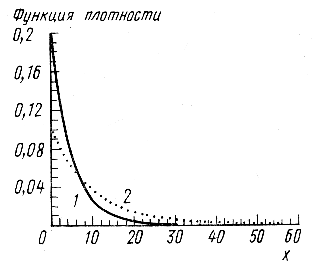
Рис. 3. Функція щільності f(x) експоненційного розподілу:
(1) Q=0.2, (2) Q=0.1
Для побудови моделі СМО виконуємо наступні дії:
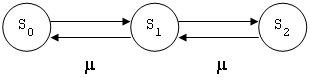
Як було сказано раніше ми будемо використовувати СМО у якості нашої моделі. Стани СМО ми будемо описувати за допомогою формул, що будуть надані нище. Побудуємо нашу СМО у вигляді графа, що зображено на рисунку 4:
l0 l1 ln-1

S0 S1 … Sn
m1 m2 mn
Рисунок 4 - схематичне представлення СМО з обмеженої чергою
Визнеачаємо всі види станів СМО
S0 – система вільна.
S1 – ЕОМ обробляє повідомлення, черги немає;
S2 – ЕОМ обробляє повідомлення, і в черзіодна заготівка.
Початкові характеристики:
- інтенсивність потоку повідомлень (λ);
- час обробки повідомлення (t).
Для визначення імовірностей станів СМО будемо використовувати такі формули [1]:
|

Імовірність знаходження системи в початковому стані, де χ має наступний вигляд:
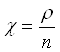 <1, (2)
<1, (2)
|
|

Імовірність знаходження системи в к-му стані (для СМО з відмовами).
|
|

Імовірність знаходження системи в r-му стані (для СМО з чергою), де m - кількість місць в черзі,
|
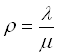
Допоміжна змінна, характеризує роботу системи.
|
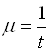
Інтенсивність потоку обробки.
Фінальні імовірності системи існують тільки за ![]() .
.
Критерії якості системи визначаються на основі критеріїв ефективності.
Середня кількість повідомлень (А), що обслуговуються СМО за одиницю часу:
|
Імовірність обслуговування повідомлення, що надійшло в СМО:
|
λ – інтенсивність потоку заявок (1/5);
μ – інтенсивність потоку обробки (1/7);
m – довжина черги (1) ;
n – кількість каналів (1);
![]() Для даної системи:
Для даної системи:
Похожие работы
... Додаток Г – Результати роботи програми, щодо перевірки коректності роботи СОП..............................................................................................20 Вступ Темою даної курсової роботи є моделювання процесу надходження повідомлень у систему обробки повідомлень від датчиків і вимірювальних пристроїв. Існує проблема оцінки функціонування довільної системи, тобто ...
... їх обробки на ЕОМ можна представити у вигляді СМО. Тобто, модель заданої системи є дискретною стохастичною системою. Виконання імітаційного моделювання вказаного процесу надходження повідомлень від датчиків до ЕОМ та їх обробки на ЕОМ потребує проведення моделювання (імітацію) всіх подій, які можуть статись – отримання інформаційних повідомлень від датчиків, вхід і звільнення пам'яті ЕОМ, втрату ...
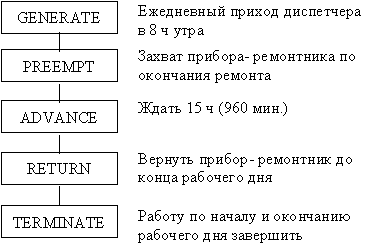
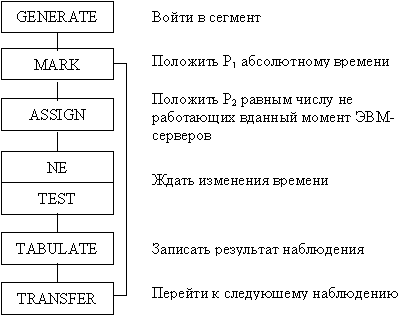
... , визначення основних характеристик одноканальних систем масового обслуговування вимагає великої обчислювальної роботи, в зв’язку з чим всі розрахунки робляться на комп’ютері. 1.2 Побудова моделей задач масового обслуговування (на прикладі роботи обчислювального центру (ОЦ)) 1.2.1 Модель для імітації виробничої діяльності ОЦ 1.2.1.1 Завдання Розробити модель для імітації виробничої ді ...
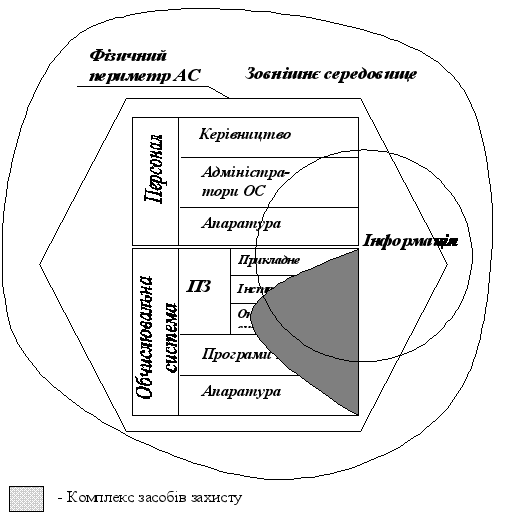
... В АБС АКБ «ПРОМІНВЕСТБАНК» ТА ОЦІНКА РІВНЯ ВРАЗЛИВОСТІ БАНКІВСЬКОЇ ІНФОРМАЦІЇ 3.1 Постановка алгоритму задачі формування та опис елементів матриці контролю комплексної системи захисту інформації (КСЗІ) інформаційних об’єктів комерційного банку В дипломному дослідженні матриця контролю стану побудови та експлуатації комплексної системи захисту інформації в комерційному банку представлена у вигляді ...
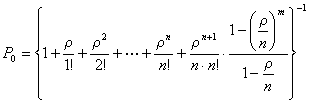

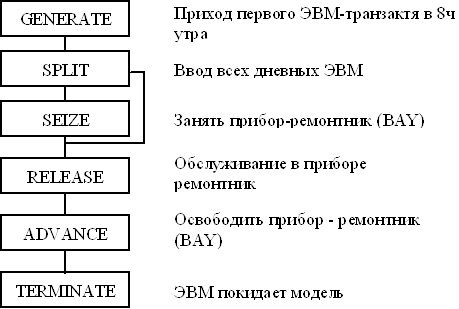

0 комментариев