Навигация
Геометрическая интерпретация
2.2 Геометрическая интерпретация
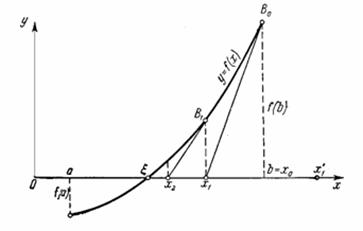
Рассмотрим график функции ![]() . Это означает, что решение уравнения
. Это означает, что решение уравнения ![]() и
и ![]() - это точка пересечения
- это точка пересечения ![]() с прямой
с прямой ![]() :
:
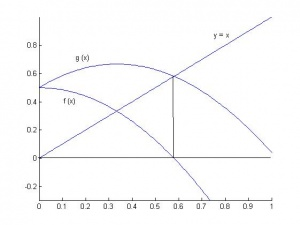
Рисунок 3.
И следующая итерация ![]() - это координата x пересечения горизонтальной прямой точки
- это координата x пересечения горизонтальной прямой точки ![]() с прямой
с прямой ![]() .
.
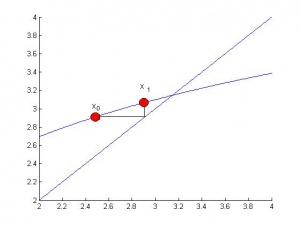
Рисунок 4.
Из рисунка наглядно видно требование сходимости ![]() . Чем ближе производная
. Чем ближе производная ![]() к 0, тем быстрее сходится алгоритм. В зависимости от знака производной вблизи решения приближения могут строится по разному. Если
к 0, тем быстрее сходится алгоритм. В зависимости от знака производной вблизи решения приближения могут строится по разному. Если ![]() , то каждое следующее приближение строится с другой стороны от корня:
, то каждое следующее приближение строится с другой стороны от корня:
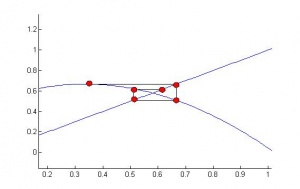
Рисунок 5.
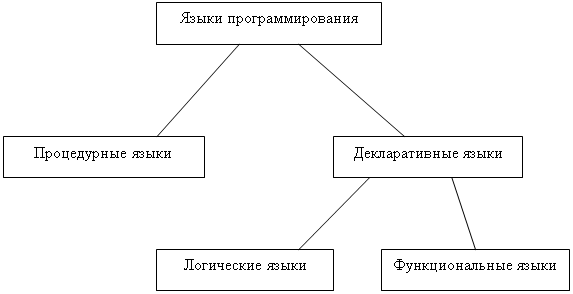
3. Функциональные модели и блок-схемы решения задачи
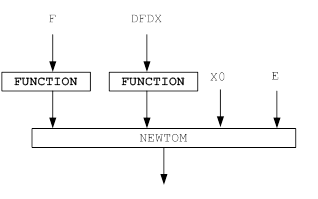
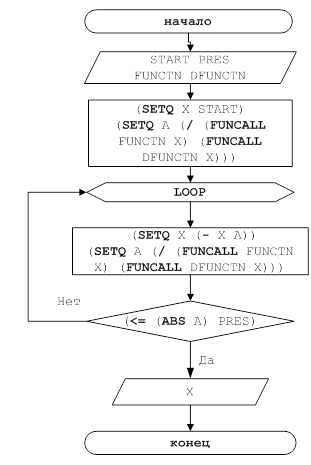
Функциональные модели и блок-схемы решения задачи представлены на рисунке 6, 7.
Используемые обозначения:
· FN, F – уравнение для поиска корня;
· X, START – начальное значение;
· E, PRECISION – точность вычисления;
· N, COUNT_ITER –количество итераций.
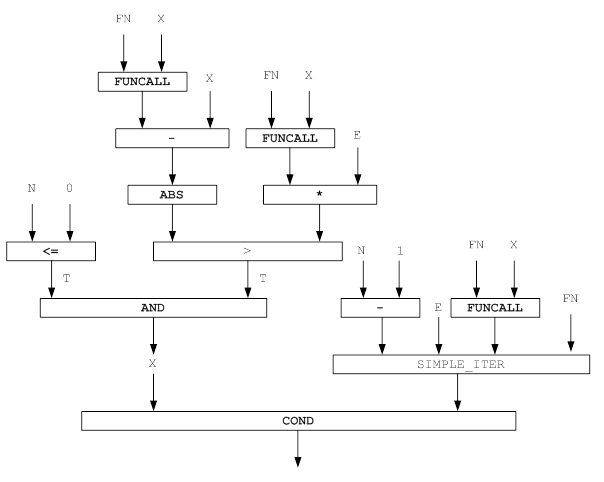
Рисунок 6 – Функциональная модель решения задачи для функции SIMPLE_ITER
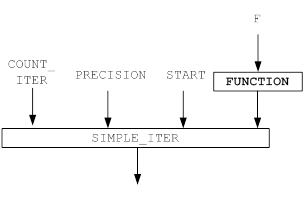
Рисунок 7 – Функциональная модель решения задачи для поиска корня уравнения методом простой итерации
4. Программная реализация решения задачи
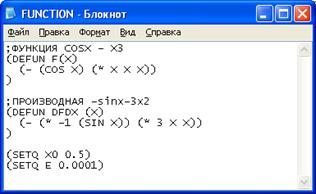
Файл SIMPLE_ITER.txt
;ФУНКЦИЯ, РЕАЛИЗУЮЩАЯ МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
(DEFUN SIMPLE_ITER (N E X FN)
(COND
((AND (<= N 0) (> (ABS (- (FUNCALL FN X) X)) (* E (FUNCALL FN X)))) X)
(T (SIMPLE_ITER (- N 1) E (FUNCALL FN X) FN))
)
)
;ПОДГРУЖАЕМ УРАВНЕНИЕ
(LOAD "D:\\FUNCTION.TXT")
;РАССЧИТЫВАЕМ НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ К КОРНЮ
(SETQ START (/ (- (CADR INTERVAL) (CAR INTERVAL)) 2))
;ВЫЧИСЛЯЕМ КОРЕНЬ
(SETQ ROOT (SIMPLE_ITER COUNT_ITER PRECISION START (FUNCTION F)))
;ОТКРЫВЕМ ФАЙЛ ДЛЯ ЗАПИСИ
(SETQ OUTPUT_STREAM (OPEN "D:\\ROOT.TXT" :DIRECTION :OUTPUT))
;ПЕЧАТАЕМ В ФАЙЛ КОРЕНЬ
(PRINT 'ROOT OUTPUT_STREAM)
(PRINT ROOT OUTPUT_STREAM)
;ЗАКРЫВАЕМ ФАЙЛ
(TERPRI OUTPUT_STREAM)
(CLOSE OUTPUT_STREAM)
Файл FUNCTION.txt (пример 1)
;ФУНКЦИЯ
(DEFUN F (X)
(/ (+ (- (* X X) (* 5 (COS X))) 3.25) 3)
)
;КОЛИЧЕСТВО ИТЕРАЦИЙ
(SETQ COUNT_ITER 100)
;ПРОМЕЖУТОК, НА КОТОРОМ ИЩЕМ КОРЕНЬ
(SETQ INTERVAL '(-0.4 0))
;ТОЧНОСТЬ ВЫЧИСЛЕНИЯ
(SETQ PRECISION 0.0001)
Файл FUNCTION.txt (пример 2)
;ФУНКЦИЯ
(DEFUN F (X)
(- (* X X) (COS X))
)
;КОЛИЧЕСТВО ИТЕРАЦИЙ
(SETQ COUNT_ITER 60)
;ПРОМЕЖУТОК, НА КОТОРОМ ИЩЕМ КОРЕНЬ
(SETQ INTERVAL '(1 1.5))
;ТОЧНОСТЬ ВЫЧИСЛЕНИЯ
(SETQ PRECISION 0.0001)
5. Пример выполнения программы
Пример 1.
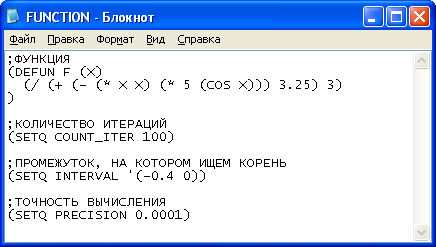
Рисунок 8 – Входные данные
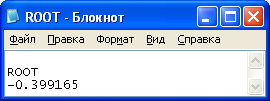
Рисунок 9 – Выходные данные
Пример 2.
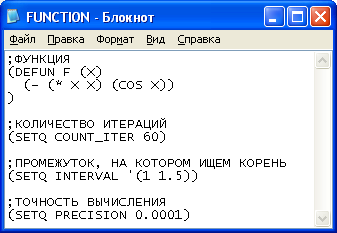
Рисунок 10 – Входные данные

Рисунок 11– Выходные данные
ЗАКЛЮЧЕНИЕ
Проблема повышения качества вычислений, как несоответствие между желаемым и действительным, существует и будет существовать в дальнейшем. Ее решению будет содействовать развитие информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования.
Итогом работы можно считать созданную функциональную модель нахождения корней уравнения методом простой итерации. Данная модель применима к детерминированным задачам, т.е. погрешностью экспериментального вычисления которых можно пренебречь. Созданная функциональная модель и ее программная реализация могут служить органической частью решения более сложных задач.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы
1. Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] / И.Н.Бронштейн, К.А.Семендяев. – М.: Наука, 2007. – 708 с.
2. Кремер, Н.Ш. Высшая математика для экономистов: учебник для студентов вузов. [Текст] / Н.Ш.Кремер, 3-е издание – М.:ЮНИТИ-ДАНА, 2006. C. 412.
3. Калиткин, Н.Н. Численные методы. [Электронный ресурс] / Н.Н. Калиткин. – М.: Питер, 2001. С. 504.
4. Поиск минимума функции [Электронный ресурс] – Режим доступа: http://solidbase.karelia.ru/edu/meth_calc/files/12.shtm
5. Семакин, И.Г. Основы программирования. [Текст] / И.Г.Семакин, А.П.Шестаков. – М.: Мир, 2006. C. 346.
6. Симанков, В.С. Основы функционального программирования [Текст] / В.С.Симанков, Т.Т.Зангиев, И.В.Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.
7. Степанов, П.А. Функциональное программирование на языке Lisp. [Электронный ресурс] / П.А.Степанов, А.В. Бржезовский. – М.: ГУАП, 2003. С. 79.
8. Хювенен Э. Мир Лиспа [Текст] / Э.Хювенен, Й.Сеппянен. – М.: Мир, 1990. – 460 с.
Похожие работы
... метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов. Целью данной курсовой работы является Лисп – реализация нахождения корней уравнения методом Ньютона. 1. Постановка задачи Дано уравнение: . Требуется решить это уравнение, точнее, найти один из его корней (предполагается, что ...
... . В частности: (8) Из (7) и (8) следует, что в M нет двух неравных натуральных чисел. Доказательство закончено. 3.2 Рекурсия Особое место для систем функционального программирования приобретает рекурсия, поскольку она позволяет учитывать значения функции на предыдущих шагах. С теоретической точки зрения рекурсивные определения являются теоретической основой всей современной ...
... , а иногда и невозможным. Недостатки MOLAP-модели: · Многомерные СУБД не позволяют работать с большими базами данных. · Многомерные СУБД по сравнению с реляционными очень неэффективно используют внешнюю память. В подавляющем большинстве случаев информационный гиперкуб является сильно разреженным, а поскольку данные хранятся в упорядоченном виде, неопределенные значения ...
0 комментариев