Нахождение корней уравнения методом Ньютона (ЛИСП-реализация)

СОДЕРЖАНИЕ

Введение

1. Постановка задачи

2. Математические и алгоритмические основы решения задачи

2.1 Описание метода

2.2 Недостатки метода

3. Функциональные модели и блок-схемы решения задачи

4. Программная реализация решения задачи

5. Пример выполнения программы

Заключение

Список использованных источников и литературы

ВВЕДЕНИЕ

Метод Ньютона (также известный как метод касательных)— это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727), под именем которого и обрёл свою известность.

Метод был описан Исааком Ньютоном в рукописи De analysi per aequationes numero terminorum infinitas (лат.Об анализе уравнениями бесконечных рядов), адресованной в 1669 году Барроу, и в работе De metodis fluxionum et serierum infinitarum (лат.Метод флюксий и бесконечные ряды) или Geometria analytica (лат.Аналитическая геометрия) в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения x_n, а последовательность полиномов и в результате получал приближённое решение x.

Впервые метод был опубликован в трактате Алгебра Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе Analysis aequationum universalis (лат.Общий анализ уравнений). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений x_n вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.

В 1879 году Артур Кэли в работе The Newton-Fourier imaginary problem (англ. Проблема комплексных чисел Ньютона-Фурье) был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.

Целью данной курсовой работы является Лисп – реализация нахождения корней уравнения методом Ньютона.

1. Постановка задачи

Дано уравнение:

.

Требуется решить это уравнение, точнее, найти один из его корней (предполагается, что корень существует). Предполагается, что F(X) непрерывна и дифференцируема на отрезке [A;B].

Входным параметром алгоритма, кроме функции F(X), является также начальное приближение - некоторое X₀, от которого алгоритм начинает идти.

Пусть уже вычислено X_i, вычислим X_i+1 следующим образом. Проведём касательную к графику функции F(X) в точке X = X_i, и найдём точку пересечения этой касательной с осью абсцисс. X_i+1 положим равным найденной точке, и повторим весь процесс с начала.

Нетрудно получить следующее выражение:

X_i+1 = X_i - F(X_i) / F'(X_i)

Интуитивно ясно, что если функция F(X) достаточно "хорошая", а X_i находится достаточно близко от корня, то X_i+1 будет находиться ещё ближе к искомому корню.

Пример 1.

Требуется найти корень уравнения , с точностью .

Производная функции  равна

.

Возьмем за начальную точку , тогда

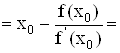-9.716215;

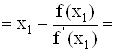5.74015;

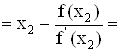3.401863;

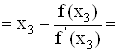-2.277028;

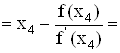1.085197;

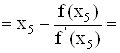0.766033;

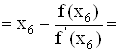0.739241.

Таким образом, корень уравнения

 равен 0.739241.

Пример 2.

Найдем корень уравнения функции методом Ньютона

cosx = x³.

Эта задача может быть представлена как задача нахождения нуля функции

f(x) = cosx − x³.

Имеем выражение для производной

.

Так как  для всех x и x³ > 1 для x > 1, очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение x₀= 0.5, тогда:

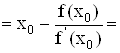1.112141;

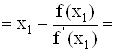0.90967;

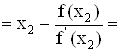0.867263;

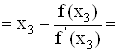0.865477;

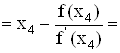0.865474033111;

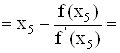0.865474033102.

Таким образом, корень уравнения функции

cosx = x³ равен 0.86547403.

Пример 3.

Требуется найти корень уравнения , с точностью .

Производная функции

 равна .

Возьмем за начальную точку , тогда

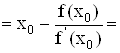-2.3;

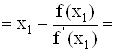-2.034615;

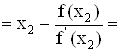-2.000579;

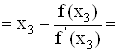-2.0.

Таким образом, корень уравнения

 равен -2.