Навигация
Нахождение допустимого решения
1. Нахождение допустимого решения.
2. Нахождение оптимального решения среди допустимых решений.
Решение симплекс-методом сопровождается так называемой симплекс-таблицой. На основе анализа таких таблиц определяется необходимость улучшения решения или отсутствие решения или нахождение оптимального решения.
Первым делом необходимо получить каноническую задачу. Преобразование общей и стандартной ЗЛП производится на основе свойств эквивалентности этих задач. При этом неравенство преобразуется в равенство путем введения дополнительной неотрицательной переменной. В результате система ограничений будет записана в виде системы линейных уравнений, где количество неизвестных больше, чем количество уравнений.
Составление первой симплекс-таблицыВ канонической задаче по количеству ограничений равенств выделяются базисные переменные. Остальные переменные называются свободными. В системе уравнений все члены со свободными переменными переносятся вправо и разрешаются.
На основании полученных выражений для базисных переменных из целевой функции исключаются все базисные переменные. Составляется симплекс- таблица по следующим правилам:
1. Первый столбец включает базисные переменные.
2. Составляется второй столбец из свободных членов.
3. Последующие столбцы составляются из коэффициентов при свободных переменных с противоположными знаками.
4. Последней строкой этой таблицы является строка целевой функции.
| Базисные переменные | Свободные члены | Свободные переменные | |||||
| x1 | x2 | … | xj | … | xn | ||
| Xn+1 | b1 | A11 | A12 | … | A1j | … | A1n |
| Xn+2 | b2 | A21 | A22 | … | A2j | … | A2n |
| ... | … | … | … | … | … | … | … |
| Xn+i | bi | Ai1 | Ai2 | … | Aij | … | Ain |
| … | … | … | … | … | … | …. | … |
| Xn+m | bm | Am1 | Am2 | … | Amj | … | Amn |
| z | 0 | -c1 | -c2 | …. | -cj | … | -cn |
Базисное решение – это решение системы линейных уравнений относительно базисных переменных, когда свободные переменные равны нулю. Все базисные переменные равны свободным членам в первой симплекс-таблице.
![]()
Признак допустимости базисных решений
- базисное решение допустимое, если оно неотрицательное;
- базисное решение допустимое, если в столбце свободных членов нет ни одного отрицательного элемента (кроме строки целевой функции).
Признак несовместимости ограничений
Ограничения несовместны, если в каждой строке, имеющей отрицательный свободный член, нет ни одного отрицательного элемента( Этот признак используется, если решение недопустимое).
Признак оптимальности
Если в строке целевой функции все элементы одного знака (кроме свободного члена), то целевая функция принимает экстремальное значение, при чем, если все элементы положительны, то - max, если отрицательны – min.
Признак неограниченности целевой функцииЦелевая функция неограничена, если в любом столбце, не удовлетворяющим признаку оптимальности, нет ни одного положительного элемента, при чем не ограничена сверху при нахождении максимума; и целевая функция не ограничена снизу при нахождении минимума, если в любом столбце, имеющем положительный элемент в строке целевой функции, нет ни одного отрицательного элемента.
Признак существования альтернативного (неединственного) решения
Оптимальное решение имеет альтернативу, если в строке целевой функции есть нулевые элементы (кроме свободных членов).
Нахождение разрешающих элементовРазрешающий элемент находится на пересечении разрешающей строки и разрешающего столбца. Разрешающая строка указывает на базисную переменную, переходящую в свободную. Разрешающий столбец указывает на свободную переменную, переходящую в базисную.
1. Разрешается столбец.
a) решение недопустимое: в любой строке, имеющей отрицательный свободный член, находится отрицательный элемент. Этот элемент находится в разрешающем столбце.
b) решение допустимое, неоптимальное: любой столбец, не удовлетворяющий признаку оптимальности, является разрешающим столбцом.
2. Разрешающая строка.
Находятся положительные отношения свободных членов к элементам разрешающего столбца. Минимальное отношение соответствует разрешающей строке.
Правила преобразования симплекс-таблицы
1. В новой таблице меняются местами по разрешающему элементу свободные и базисные переменные:
![]()
2.Ячейка разрешающего элемента заполняется обратным знаком:

3. Разрешающая строка делится на разрешающий элемент:
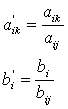
4. Элементы разрешающего столбца делятся на разрешающий элемент с противоположным знаком:
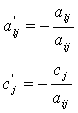
5. Из остальных ячеек вычисляется произведение элементов, стоящего на соответствующем разрешающем столбце и соответствующей разрешающей строке, деленные на разрешающий элемент:
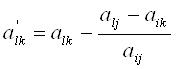
Динамическое программирование
Динамическое программирование используется для исследования многоэтапных процессов. Состояние управляемой системы характеризуется определенным набором параметров (фазовыми координатами). Процесс перемещения в фазовом пространстве разделяют на ряд последовательных этапов и производят последовательную оптимизацию каждого из них, начиная с последнего. На каждом этапе находят условное оптимальное управление при всевозможных предположениях о результатах предыдущего шага. Когда процесс доходит до исходного состояния, снова проходят все этапы, но уже из множества условных оптимальных управлений выбирается одно наилучшее. Получается, что однократное решение сложной задачи заменяется многократным решением простой. Важно, что значения критерия – сумма частных значений, достигнутых на отдельных шагах, и предыстория не имеют значения при определении будущих действий .
Особенности методов и моделей динамического программирования
1. Принятие оптимального решения рассматривается как процесс многоэтапный.
2. Показатель эффективности всего процесса управления является аддитивной функцией показателей эффективности каждого шага.
![]()
3. Выбор управления на k-том шаге зависит только от состояния системы к этому шагу и не влияет на предшествующие шаги.
4. Состояние Sk зависит только от состояния предшествующего шага и управления xk.
5. На каждом шаге управление зависит от конечного числа переменных, а состояние системы от конечного числа параметров.
Принцип оптимальности Беллмана
Свойства динамического программирования являются следствием общего принципа, сформулированного Р. Беллманом и называемого принципом оптимальности: оптимальная политика обладает тем свойством, что каковы бы ни были первоначальные состояния и первоначальные решения, последующие решения должны основывать оптимальную политику относительно состояния, полученного в результате полученного решения.
Знание принципа оптимальности полезно уже хотя бы потому, что формирует правильную профессиональную психологию. Но, конечно, не только поэтому: решение многих задач базируется на нем.
Формулы Беллмана для динамического программирования
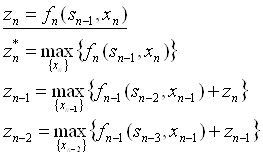

ГЛАВА 3. ПРАКТИЧЕСКОЕ ОБОСНОВАНИЕ ТЕОРИИ
Линейное программирование с использованием пакета прикладных программ Math Cad.
Нахождение оптимального плана производства в первый год осуществляется с помощью прикладной программы Math Cad.

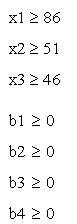
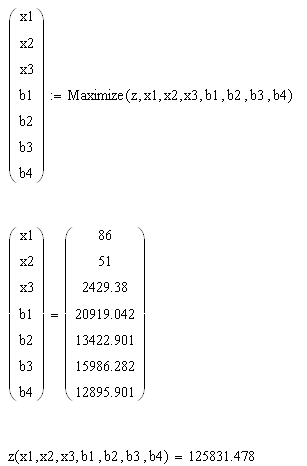
Во второй год:



![]()
В третий год:
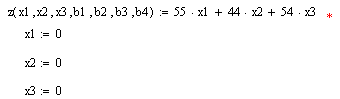

В четвертый год:


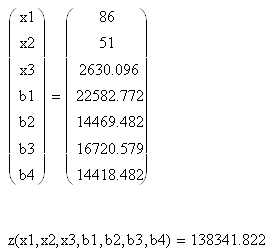
В пятый год оптимальный план производства:


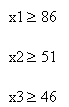

Динамическое программирование с помощью программы Microsoft Excel
| x | Показатель эффективности предприятия | |||||||||
| f(x1) | f(x2) | f(x3) | f(x4) | f(x5) | z1 | z2 | z3 | z4 | z5 | |
| 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 80000,0 | 15206,1 | 15671,5 | 16246,9 | 16514,4 | 16653,6 | 15206,1 | 15671,4 | 16246,9 | 16514,4 | 16653,6 |
| 100000,0 | 19815,5 | 20769,5 | 21384,9 | 21590,6 | 21737,7 | 19815,5 | 30877,6 | 31918,4 | 32761,3 | 21737,7 |
| 110000,0 | 22120,2 | 23318,5 | 23953,8 | 24128,6 | 24279,7 | 22120,2 | 35975,6 | 37056,3 | 37899,3 | 33168,1 |
| 120000,0 | 24424,9 | 25867,6 | 26522,8 | 26666,7 | 26821,7 | 24424,9 | 40585,04 | 42154,4 | 43037,3 | 43328,2 |
| 150000,0 | 31389,0 | 33514,6 | 34229,8 | 34280,9 | 34447,8 | 31389,0 | 43134,06 | 44723,4 | 45544,4 | 45870,2 |
Получается, что денежные средства распределяются только на один год, так как показатель эффективности увеличивается с каждым годом. Значит, инвестиции следует вложить в пятый год.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. В.М.Трояновский. Математическое моделирование в менеджменте, уч. пособие. 2-е изд., испр. и доп. – М.: Издательство РДЛ. 2002. – 256 с.
2. Теоретические лекции под руководством Смирнова Ю.Н.
3. Методические пособия.
4. Пакеты прикладных программ Math Cad, Microsoft Excel, Microsoft Word.
Похожие работы
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
0 комментариев