Навигация
Кинематический анализ механизма транспортирования ткани
Кинематический анализ механизма верхней и нижней реек швейной машины 131-42+3 класса.
Реферат
Отчет с., 1 ч., 46 рис., 3 табл., 88 источников, 1 прил.
ШВЕЙНАЯ МАШИНА, МЕХАНИЗМ ТРАНСПОРТИРОВАНИЯ, ВЕРХНЯЯ РЕЙКА, НИЖНЯЯ РЕЙКА, ШАГ ТРАНСПОРТИРОВАНИЯ, КИНЕМАТИЧЕСКИЙ АНАЛИЗ
Объектом исследования является механизм транспортирования ткани швейной машины 131-42+3 класса, с транспортированием ткани верхней и нижней рейками.
Цель работы – разработка математического, алгоритмического и программного обеспечения для исследования кинематики механизма транспортирования швейной машины 131-42+3 класса. В результате выполнения работы были разработаны алгоритмы кинематического анализа привода нижней и верхней рейки. Так как механизмы привода нижней и верхней рейки представляют собой сложные многозвенные рычажные механизмы с разветвленными кинематическими цепями, то для их кинематического анализа используется погруппный способ. Для этого механизм был разбит на привод верхней и нижней рейки, каждый из этих приводов был разбит на кинематические цепи горизонтальных и вертикальных перемещений рейки, а указанные кинематические цепи были разбиты на структурные группы Ассура. С помощью алгоритмического обеспечения была составлена программа и получены графики траектории движения нижней и верхней реек без учёта силового замыкания последних через ткань в процессе транспортирования.
Содержание 1. Обзор литературных источников по исследованию кинематики рычажных механизмов1.1 Обзор литературных источников по кинематическому анализу и синтезу механизмов.
1.2 Обзор литературных источников по исследованию реечных механизмов транспортирования ткани швейных машин.
1.3 Обзор алгоритмов подпрограмм кинематического анализа структурных групп Ассура, входящих в кинематические схемы транспортирующих механизмов.
1.3.1 Алгоритм программы кинематического анализа кривошипа
1.3.2 Алгоритм программы кинематического анализа звена механизма первого порядка
1.3.3 Алгоритм программы кинематического анализа двухповодковой структурной группы Ассура первой модификации
1.3.4 Алгоритм программы кинематического анализа двухповодковой структурной группы Ассура второй модификации
1.3.5 Алгоритм программы кинематического анализа двухповодковой структурной группы Ассура третей модификации
1.3.6 Алгоритм программы определения величины шага транспортирования.
1.3.7 Алгоритм головного модуля программы, объединяющего в себе описанные подпрограммы в единую программу кинематического анализа.
2. Алгоритм исследования кинематики нижней рейки машины 131-42+3 класса.
2.1 Конструкционная схема механизма транспортирования ткани машины 131-42+3 класса2 . 2 Алгоритм кинематического анализа движения нижней рейки механизма транспортирования ткани швейной машины 131-42+3 класса.
3. Алгоритм исследования кинематики верхней рейки машины 131-42+3 класса.
4. Разработка алгоритмического обеспечения для исследования кинематики верхней и нижней рейки машины 131-42+3 класса.
5. Исследование кинематики механизма верхней и нижней реек 131-42+3 класса.
6. Организация работ по охране труда на предприятии.
6.1 Производственная санитария.
6.2 Основные требования по технике безопасности предъявляемые к швейным машинам.
6.3 Вентиляция и кондиционирование воздуха.
6.4 Мероприятия по снижению шума.
6.5 Организационные мероприятия, направленные на обеспечение электробезопасности.
6.6 Технические средства предупреждения пожаров и взрывов на производстве.
6.7 Мероприятия по обеспечению пожарной безопасности.
Заключение.
Список использованных источников
Приложения.
В ведениеШвейная промышленность играет важную роль непосредственно в жизни каждого человека, и поэтому состояние швейной промышленности в государстве отражается на каждом его гражданине. Развитие швейной отрасли в различных направлениях, как в области модернизации швейного оборудования, так и в области совершенствования технологии швейного производства, положительно отражается на благосостоянии каждого человека. Модернизация и повышение надежности швейного оборудования приведет к снижению себестоимости и увеличению качества швейных изделий.
Машиностроение для легкой промышленности должно обеспечивать выпуск машин, автоматов и автоматических линий, внедрение которых в производство значительно повышало бы производительность труда, улучшало качество и снижало стоимость выполняемых технологических процессов. Машины должны быть возможно долговечнее и надежнее, эстетически правильно оформлены, иметь совершенные средства по охране труда и окружающей среды.
Удовлетворение потребности населения в разнообразной модной одежде требует мобильных методов ее изготовления, что в значительной степени зависит от швейного оборудования. В швейной промышленности в настоящее время используются разнообразные швейные машины универсального и специального назначения. Тем не менее, сохраняется потребность в разработке новых, более совершенных, энерговооруженных. Высокоскоростных швейных машин и модернизации существующих. Существенную роль играет фактор времени, которое затрачивается на проектирование, разработку конструкторской и технологической документации, изготовление доводку и внедрение машины. Применение на всех указанных стадиях ЭВМ позволяет расширить возможности конструкторских бюро и машиностроительных предприятий, сократить время на разработку и внедрение новой техники, удешевить производство, сделать выпускаемые швейные машины конкурентоспособными.
По назначению машины швейных производств разделяются в основном на машины для выкраивания деталей и обработки их резанием, для формования деталей и узлов изделий, для их соединения и для отделки изделий.
Большие трудности при создании швейных машин вызывает разработка механизма транспортирования ткани (транспортирующего механизма), являющегося одним из наиболее сложных и нагруженных. Наиболее распространены рычажные механизмы транспортирования ткани реечного типа, рабочим органом которых является зубчатая рейка (рейки). Данная дипломная работа посвящена изучению и кинематическому анализу реечных механизмов транспортирования ткани швейных машин, с целью повышения качества строчки, а, следовательно, швейных изделий.
1. Обзор литературных источников по исследованию кинематики рычажных механизмов. 1.1 Обзор литературных источников по кинематическому анализу и синтезу механизмов.Суть задачи кинематического анализа рычажных механизмов состоит в определении функций положений, первых и вторых передаточных функций звеньев (их обобщенных координат) в виде функции от обобщенной координаты входного звена, движение которого считается заданным. Все существующие методы кинематического анализа условно можно разделить на графические, графоаналитические и аналитические. К наиболее ранним методам кинематического исследования механизмов относятся графические и графоаналитические. Они достаточно просты, наглядны и позволяют решить задачу анализа практически любого механизма, однако трудоемки в исполнении и обладают большой погрешностью. Аналитические методы анализа связаны с большим объемом вычислений. В связи с развитием вычислительной техники эти методы получили в последнее время наибольшее распространение, поэтому ниже более подробно остановимся именно на них.
Независимо от класса рычажного механизма определение первой и второй передаточной функций обычно сводится к решению системы линейных уравнений и, как правило, не вызывает затруднений. Описание методов решения подобных систем уравнений можно найти в любой справочной литературе по математике [1]. Решение задачи о положении звеньев механизма зависит от класса рычажного механизма: для механизма второго класса, независимо от числа звеньев, эта задача решается в явном виде, для рычажных механизмов более высоких классов - существенно усложняется.
Рассмотрим некоторые из известных методов решения задачи о положениях. Наиболее широкое применение нашел метод замкнутых векторных контуров, предложенный В.А.Зиновьевым [2]. Метод основан на представлении кинематической цепи в виде нескольких векторных контуров, проектирование которых на координатные оси, как правило, приводит к системе нелинейных уравнений относительно обобщенных координат звеньев механизма. Эта система нелинейных уравнений может быть решена аналитическими (как правило, для простых кинематических цепей), либо численными способами. Н.И.Левитский в работе [3] предлагает находить численным способом искомые углы только для начального положения механизма, а для каждого из последующих, в качестве первого приближения использовать уточненные значения углов, полученные для предыдущего положения.
Метод векторных контуров находит широкое применение при анализе механизмов второго класса, а также при анализе шестизвенных механизмов третьего и четвертого классов с различным сочетанием вращательных и поступательных пар. Э.Е.Пейсах [4] предлагает свести исходную нелинейную систему уравнений к одному алгебраическому уравнению. Применение данного способа к шестизвенным шарнирным механизмам с четырехзвенными группами Ассура двух разновидностей показано в работе [5]. Задача определения положений по этому методу сводится к отысканию вещественных корней алгебраического уравнения шестой степени. Данным способом можно определять границы некривошипных сборок, число вариантов сборки механизма, при фиксированном положении входного звена.
Ю.Ф.Морошкин [6] для составления уравнений замкнутости векторных контуров предложил метод преобразования координат. Согласно этому методу, с каждым звеном механизма связывается своя система координат, и составляются уравнения их преобразования. Уравнения имеют матричную форму, удобную для вычислений на ЭВМ и позволяют получить координаты точки, находящейся на одном звене, в системе координат, связанной с каким‑либо другим звеном.
Метод “инверсии” (иначе ‑ метод “перемены ведущего звена”, метод “замены начального звена”) [2] основан на свойстве некоторых механизмов, состоящих из групп Ассура, менять свой класс в зависимости от того, какое из звеньев механизма принято за входное. Для некоторых механизмов метод позволяет получить структуру с более простыми группами Ассура (меньшее число звеньев): например, шестизвенный механизм третьего класса можно рассматривать как механизм второго класса. Примеры применения этого метода связаны лишь с шестизвенным механизмом с трехповодковой группой.
Известен метод “размыкания кинематической цепи” (метод геометрических мест, метод ложных положений), разработанный И.И.Артоболевским [13]. Следуя этому методу, в кинематической цепи размыкаются один или несколько шарниров, что позволяет вместо одной, сложной по структуре цепи, рассматривать несколько более простых. Для каждого разомкнутого шарнира строятся возможные геометрические места его положений, как принадлежащего двум различным более простым цепям, которые он ранее соединял между собой. Действительное положение разомкнутых шарниров (а, следовательно, и всей цепи) определится пересечением соответствующих геометрических мест точек размыкания.
По методу “вставки звена” предложенным В.В.Добровольским [3], из исследуемой кинематической цепи (механизм или группа Ассура) отбрасывается одно или несколько звеньев, пока оставшаяся цепь не распадется на ряд механизмов более простой структуры. Звеньям полученных механизмов придают движение, определяя такие их положения, при которых можно будет “вставить” удаленное звено.
Интерес представляет метод “условных обобщенных координат”, предложенный У.А.Джодасбековым [8]. Этот метод представляет собой объединение метода “инверсии” с методом “вставки звена” в численно‑аналитической форме с использованием метода “преобразования координат” в матричной форме. Метод позволяет провести анализ группы Ассура любого класса и порядка, с его помощью могут быть решены задачи о числе вариантов сборки механизма, условиях существования кривошипа и др.
Для решения задачи о положениях можно применять метод “треугольников” О.Г.Озола [9]. Метод связан с возможным представлением любого замкнутого контура в виде треугольников, причем эти треугольники могут быть, как изменяемыми, так и неизменяемыми. Расчетная схема обычно состоит из трансцендентных уравнений трех типов и требует для своего решения знания приближенного положения звеньев. Автор предлагает решать систему численным способом. Известна другая форма применения метода “треугольников” [4].
Как правило, каждый из изложенных методов предназначен для решения задачи анализа конкретного класса механизмов, либо структурных групп. Пока не существует единого способа, который мог бы позволить решить задачу кинематического анализа рычажного механизма произвольной структуры в полной постановке.
Перейдем к анализу методов синтеза рычажных механизмов, в развитие которых большой вклад внесли: И.И.Артоболевский, З.Ш.Блох, А.З.Зиновьев, Н.И.Левитский, Э.Е.Пейсах и др. Целью кинематического синтеза рычажного механизма является определение постоянных параметров его кинематической схемы, исходя из сформулированной заранее постановки задачи синтеза. Методы решения задач синтеза рычажных механизмов, как правило, являются приближенными. По способу реализации их можно разделить на аналитические, графоаналитические и графические. Ниже рассмотрим только аналитические методы, которые можно разделить на аппроксимационные и оптимизационные.
Рассмотрим подробнее исследования в области аналитического синтеза многозвенных плоских рычажных механизмов. В цикле работ Э.Е.Пейсаха [10, 11] на основе кинематических возможностей шестизвенного шарнирного механизма второго класса первой модификации поставлены и аналитически решены часто встречающиеся на практике типы задач синтеза этого механизма, в том числе задача о выстое выходного звена в крайнем положении. Задачи синтеза шестизвенного шарнирного механизма второго класса второй модификации более трудны. Особый интерес представляет задача синтеза механизма с выстоем выходного звена в крайнем или промежуточном положении. Известны различные подходы к решению указанной задачи: одни авторы ищут на шатуне базового четырехзвенника точку, описывающую дугу окружности [12], другие используют l‑образный механизм Чебышева [13].
Данная задача может быть решена с помощью квадратического приближения, при этом В.И.Доронин [14] использовал семь параметров, а Э.Е.Пейсах [15] - три. В одной группе работ механизм шестизвенника делится на диаду и четырехзвенник, в шатунной плоскости которого ищется круговая квадратическая точка, с целью последующего присоединения диады. Для поиска круговой квадратической точки используется метод инверсии или метод обращения движения [16]. В другой группе работ шестизвенник также делится на диаду и четырехзвенник, но синтезируется диада [17]. В третьей группе работ в механизме шестизвенника “изымается” одно из звеньев и ищется возможность его “вставки”. Здесь можно отметить метод “вставки двухпарного звена” предложенный Э.Е.Пейсахом [15].
В работе [18] применительно к синтезу регулируемых механизмов, воспроизводящих заданные шатунные кривые, излагается метод “комплексных чисел”. Задача решена аналитически для траекторий, точки которых разделены конечными интервалами времени, а также для траекторий имеющих бесконечно близкие точки. Предлагаемый метод позволяет синтезировать регулируемые механизмы, реализующие движение изображающей точки вдоль различных аппроксимаций прямых линий, траекторий с различной кривизной, касательных к траектории, а также некоторых произвольных траекторий. Рассмотрены четырехзвенные механизмы и предложены методы их синтеза.
Ю.Л.Саркисян [19] предлагает выполнять синтез плоских шарнирных механизмов методом квадратического приближения функции. Метод квадратического приближения для синтеза четырех‑ и шестизвенного шарнирных направляющих механизмов рассмотрен в работе [20].
В ряде работ [21], [22] для синтеза шатунной кривой и статического расчета механизма применяется метод Гаусса. С целью воспроизведения плоских кривых и при кинематическом синтезе кривых высших порядков применительно к четырехзвенным механизмам [23] использовался ослабленный метод наименьших квадратов Левенберга.
Большое количество работ посвящено решению задач оптимизационного синтеза рычажных механизмов. В работах [24],[25],[26] для формирования траекторий и воспроизведения функций, а также для решения задач управления при помощи плоских механизмов были использованы методы случайного поиска.
Вклад в задачу оптимального синтеза механизмов внесли R.L.Fox и K.D.Willmert [28]. Они ввели ограничения типа неравенств, которые оказались подходящими для применения процедуры динамического программирования [29]. R.E.Gustavson [30] использовал весовые коэффициенты к трем необходимым критериям отбора решений задачи Бурместера с четырьмя кратно‑раздельными положениями механизма. В работе [31] D.W.Levis и C.K.Gyory изложили другой оригинальный подход к задаче синтеза направляющих механизмов, связанный с использованием “затухающей” итерации по методу наименьших квадратов.
В работе C.Bagsi и J.Lee [32] предложен метод оптимального синтеза плоских механизмов, воспроизводящих траектории и положения твердого тела. Метод разработан для плоского четырехзвенного механизма, у которого неизвестны шесть или восемь размеров. Искомые размеры оптимального механизма определяются путем минимизации ошибки в уравнениях замыкания контура для N расчетных точек траектории, а также в уравнении механизма, где не ограничено число неизвестных размеров системы. Линеаризация расчетных уравнений выполняется методом линейной суперпозиции. Решение уравнений не требует итераций и дает ряд оптимальных механизмов с различной степенью приближения.
Вариационный метод синтеза одно‑ и многоконтурных плоских механизмов с одной степенью свободы, предназначенных для управления движением твердых тел через заданные положения на плоскости предложен Э.Е.Пейсахом [33]. Посредством минимизации целевой функции, представляющей собой сумму квадратов ошибок в вычислительных координатах двух точек тела, определены оптимальные размеры механизма. Решение расчетных уравнений производится матричным методом итерации и релаксационным методом Гаусса. Для плоского механизма, воспроизводящего плоскую траекторию, задачу синтеза удается свести к задаче оптимизации, накладывая ограничения, обеспечивающие совмещение двух точек тела. Для управления движением твердого тела и воспроизведения траектории точки этого тела синтезированы шестизвенный механизм Стефенсона типа I и плоский четырехзвенный шарнирный механизм.
В статье [34] рассмотрен процесс оптимизации, в котором исследованы результаты, полученные при моделировании на АВМ движения плоского шарнирного четырехзвенника. Показана сложность аналитического выражения для шатунной кривой, что обусловливает необходимость применения сложного метода при синтезе этой кривой. Показано, что минимизация ошибки согласования между требуемой и полученной шатунными кривыми достигается с помощью комбинации релаксационного и градиентного методов.
D.W.Levis и C.K.Gyory в работе [35] показывают, что траектория точки шатуна плоского механизма является кривой, которую можно описать рядом парных координат. Последовательный подбор параметров конкретного механизма осуществляется методом “затухающих наименьших квадратов”. Последовательное применение этого метода дает оптимальное приближение к заданной кривой, описываемой рядом парных координат. В качестве примера этот метод был применен к четырехзвенному механизму.
Задача синтеза шарнирного четырехзвенного механизма в работе [35] представлена как задача математического программирования, которая заключается в проектировании шарнирного четырехзвенника, присоединительная точка которого описывает заданную кривую с наибольшей точностью, а повороты кривошипа с возможно большей точностью соответствуют требуемым значениям. При этом накладывается ряд ограничений: на размеры звеньев механизма, на положения шарнирных точек, на величины сил и моментов звеньев механизма и т.д. Решение авторы получают методом итераций с помощью ЭВМ. Приведены примеры механизмов, воспроизводящих прямую линию, кривую в форме восьмерки и дугу окружности.
В работах Э.Е.Пейсаха [4], [36] дано систематическое изложение оптимизационного синтеза плоских рычажных механизмов. В этих работах показана возможность при синтезе наряду с воспроизведением заданного движения (главного условия), учесть и дополнительные условия, характеризующие критерии качества и имеющие обычно форму неравенств. К таким условиям, например можно отнести: существование механизма, конструктивные, кинематические, динамические и иные ограничения. В работе [4] Э.Е.Пейсах предложил “обратно градиентный” метод поиска, который позволяет учесть такие неблагоприятные особенности целевой функции, как нелинейность, многоэкстремальность, наличие оврагов на ее гиперповерхности и др.
Задачи синтеза в ряде случаев могут быть решены на базе метода “блокируемых зон” [4]. Данный метод предполагает получение в аналитической форме не только собственно решения задачи синтеза, но и областей существования решений (блокируемых зон). В соответствии с этим методом в результате решения задачи синтеза в аналитическом виде могут быть получены области возможных значений задаваемых и свободных параметров механизма.
Из приведенного обзора литературных источников следует, что большинство современных аналитических методов кинематического анализа и синтеза рычажных механизмов основано на применении широких возможностей вычислительной техники, для чего разрабатывается соответствующее программное обеспечение. В настоящее время существует большое число пакетов программ, посвященных кинематическому анализу и синтезу рычажных механизмов [38],[39],[40],[41],[42],[43],[44]. В табл. 1.1. представлены некоторые наиболее существенные из последних разработок в этой области. Следует отметить, что в основном они пригодны для кинематического анализа плоских рычажных механизмов (разработаны общие алгоритмы [4] и программы анализа на ЭВМ). Для механизмов достаточно сложной структуры, решение задач кинематического анализа с помощью этих программ практически невозможно. Синтез рычажных механизмов имеет еще более высокую сложность и зависит от поставленной конструктором задачи, структуры синтезируемого механизма и множества условий (ограничений). Существующие программы синтеза рычажных механизмов в большинстве своем ориентированы на решение задач определенного конкретного класса (например, синтез четырехзвенного передаточного механизма, шестизвенного механизма с выстоем [4] и т.п.) и также не могут претендовать на общность. Исходя из сказанного, следует, что в будущем для новых достаточно сложных рычажных механизмов необходимо разрабатывать новые пакеты программ для решения конкретных задач анализа и синтеза в зависимости от технологических и конструктивных требований к ним.
| Таблица 1.1. Программы кинематического анализа и синтеза рычажных механизмов на ПЭВМ. |
| |
| ||
| Название пакета | Краткое описание возможностей | |
| GISK-4000 | Система синтеза плоских рычажных механизмов, включающая модули: ANEK – анализа кинематики; IBSE – ввод структуры механизма; GIKO – выдача результатов в графической форме. | |
| CUED | Пакет программ кинематического анализа механизмов. Пакет позволяет производить кинематический анализ механизма (состоит из процедур написанных на языке программирования Фортран). | |
| КАМ | Кинематический анализ плоских рычажных механизмов, включающих в себя двухповодковые структурные группы первых трех модификаций. | |
| KSM | Решение задач синтеза четырехзвенных и шестизвенных рычажных механизмов. | |
| ALBUM | Компьютерный альбом по рычажным механизмам. | |
| SYNMECH | Синтез шестизвенного рычажного механизма с выстоем. | |
| LINKAGES | Компьютерная система структурного и кинематического анализа рычажных механизмов (включает в себя базу знаний по рычажным механизмам). | |
| RECSYN | Оптимизационный синтез четырехзвенных механизмов по двум, трем или четырем точным положениям . | |
| KINEMA 5 | Кинематический анализ плоских рычажных механизмов. | |
Механизм транспортирования ткани относится к основным механизмам швейной машины, поэтому практически любая литература, посвященная проектированию швейных машин, содержит разделы, связанные с его конструкцией или проектированием. Среди наиболее известных следует отметить работы А.Н.Архипова [46],[47], Н.М.Вальщикова [48], В.П.Гарбарука [49], А.И.Комиссарова [50], Е.А.Маракушева [51], В.П.Полухина [52],[53],[60], Л.Б.Рейбарха [54].
Кроме указанных работ существует большое количество публикаций, посвященных исследованиям транспортирующих механизмов швейных машин. Их анализ позволяет выделить следующие направления в исследованиях транспортирующих механизмов:
- анализ структуры и конструкций;
- кинематический анализ;
- синтез и оптимизация;
- экспериментальные исследования;
- исследования динамики.
Анализу структуры и конструкций транспортирующих механизмов швейных машин посвящены работы S.Mende [61], М.М.Закарая и др. [62], В.И.Дзюба и др. [63], В.П.Полухина, Л.К.Милосердного [53],[64], Б.С.Сункуева и др. [65], Ю.Ю.Щербаня и А.В.Горобца [66],[67],[68],[69]. S.Mende в работе [61] привел анализ конструкций механизмов транспортирования ткани реечного типа. Отмечено, что в качестве привода рейки, как правило, используются шести и восьмизвенные рычажные механизмы с высшими и низшими кинематическими парами. Статья М.М.Закарая и др. [62] посвящена анализу структурных ошибок в механизмах перемещения материала машин беспосадочного шва. В этой работе рассмотрены условия обеспечения синхронности перемещений рейки и иглы.
В.И.Дзюба и Б.В.Орловский [63] предлагают свой метод выбора кинематической схемы транспортирующего механизма, реализованный при разработке специальной швейной машины для прошивки и сборки застежки-молнии. Для этого авторы на основе анализа требований, предъявляемых к механизму, и на основании опроса мнений экспертов, построили статистическую регрессионную модель, описывающую зависимость обобщенного критерия качества от функциональных, эксплуатационных и экономических показателей (наличие кинематического разрыва в месте взаимодействия рабочего органа и спирали молнии, возможная степень регулирования величины шага продвижения спирали, количество звеньев механизма, количество высших кинематических пар, уровень шума, вибрации и др.). Анализ полученной модели, позволил выделить наиболее существенные параметры, описывающие качество механизма и, изменяя их, выбрать оптимальную кинематическую схему.
Сравнительный анализ механизмов перемещения с точки зрения снижения нагрузки на распределительный вал швейной машины приведен в статье Ю.Ю.Щербаня и В.А.Горобца [66]. В этой статье авторы на основе результатов исследования динамики транспортирующего механизма швейной машины 1022М кл. предлагают структурную схему механизма транспортирования, обеспечивающую уменьшение нагрузки на распределительный вал швейной машины.
В работах Л.К.Милосердного, В.П.Полухина, Б.С.Сункуева [53],[64], [65] рассмотрено построение конструктивно-унифицированных рядов швейных машин. При этом важна тщательная разработка структурной, кинематической и конструктивной схемы механизма (в том числе и механизма транспортирования ткани) базовой машины ряда.
С точки зрения структуры большой интерес представляют механизмы вертикального дифференциала. В этих механизмах в момент перемещения материалов возможен так называемый эффект “перепляса” прижимной лапки [66]. Ю.Ю.Щербань и В.А.Горобец в статье [66] предлагают в момент перемещения материалов механизм такого типа рассматривать как механизм, одним из звеньев которого является транспортируемый материал. В работе описывается алгоритм анализа структуры подобных механизмов. Продолжая эту тему, авторы в работах [68],[69] предлагают классификацию способов перемещения материалов верхней и нижней рейками по характеру воздействия рабочих органов транспортирования на материал. На основе анализа способов воздействия рабочих органов транспортирования на материал предлагается система изменения модификаций механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции.
Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца [71] с помощью мини-ЭВМ проведен кинематический анализ механизма вертикального дифференциала машины 897 кл., структура которого меняется в течении рабочего цикла (транспортирования и холостого хода). В статье Zhao Xifang, Zhang Zongming [72] проведено исследование механизма транспортирования на примере машины челночного стежка FB2-1 кл. Отмечается, что механизм транспортирования этой машины в составе кинематической цепи подъема и подачи содержит трехцентровые кулачки. С помощью разработанной программы для ЭВМ производится: оценка изменения траектории движения рейки в зависимости от регулировок механизма; оптимизация траектории движения рейки, в результате которой обеспечивается прямолинейный участок траектории рейки во время рабочего хода. В статье Ю.Ю.Щербаня и В.А.Горобца [74] предложена методика поэтапного определения кинематических характеристик трехповодковых групп, одним из звеньев в которых является транспортируемый материал. Разработано соответствующее программное обеспечение.
Проектирование механизмов транспортирования основано, как правило, на оптимизационных методах синтеза. В статье В.Ф.Ермолаева, В.А.Лишанкова и др. [76] предложена методика определения оптимальных параметров реечного механизма подачи материала, исходя из условий минимизации горизонтальной составляющей скорости зубьев рейки в начале и конце перемещений. В работе Б.С.Сункуева [77] рассмотрен синтез регулируемого шестизвенного механизма, входящего в состав кинематической цепи продвижения транспортирующего механизма. Синтез механизма произведен графоаналитическим методом по заданным функциям регулирования и дополнительным условиям.
Постановка и особенности решения задач оптимизации параметров регулируемых двенадцатизвенных механизмов подачи материала швейных машин рассмотрены в работе В.Ф.Ермолаева и В.А.Новгородцева [78]. Приводятся результаты оптимизации и отмечается, что требования, предъявляемые к механизмам подачи различны в зависимости от скоростных характеристик машины.
Оптимизация механизма транспортирования по функциональным зависимостям углов передачи приведена в статье В.Ф.Смирновой, В.П.Шерстнева и Б.С.Сункуева [79]. Дано аналитическое решение задачи с учетом конструктивных ограничений. В статье Ю.Ю.Щербаня и В.А.Горобца [81] рассмотрена оптимизация параметров механизма транспортирования по критерию минимума рассогласования движения рабочих органов (на фазе транспортирования). Разработан пакет прикладных программ.
Оптимизационный синтез механизма транспортирования рассмотрен и в работе Peisun Ma [81]. Оптимизация проводится с учетом минимизации отклонений траектории рейки механизма от требуемой и учетом условий процесса стежкообразования. Оптимизация была реализована на ЭВМ методом последовательных приближений.
Значительное количество работ посвящено экспериментальным исследованиям транспортирующих механизмов швейных машин. В статье O.Masanori и S.Hiroshi [82] приведены результаты исследования траектории движения рейки. Для регистрации траектории движения рейки авторы использовали лазерный датчик, для чего была разработана специальная экспериментальная установка. В результате произведенных исследований определено влияние на траекторию движения рейки скорости шитья.
Исследованию процесса продвижения материала на высокоскоростных швейных машинах посвящена работа Л.Б.Рейбарха и В.П.Полухина [83]. В ней приведены результаты экспериментального исследования влияния на длину стежка частоты вращения главного вала, силы давления прижимной лапки на материал и массы материала. В качестве объекта исследования выбрана двухигольная плоскошовная швейная машина 1876 кл. Эксперимент проводился на сложенной вдвое ленте из бязи шириной 50 мм (ГОСТ 11680-76, арт. 201). Частоту вращения главного вала машины варьировали в пределах (2000¸6000) мин-1. Массу материала имитировали последовательным нагружением горизонтально расположенной ленты гирями массой 0.5 и 1.0 кг. Давление прижимной лапки в ходе эксперимента изменяли в пределах (20¸60) Н. Номинальная длина стежка устанавливалась равной 3 мм.
Результаты исследования показали, что зависимость длины стежка от частоты вращения главного вала машины в диапазоне (2000¸6000) мин-1, как правило, имеет максимум. Уменьшение давления лапки с 60 Н до 20 Н смещает максимум к началу координат и приводит к резкому уменьшению длины стежка при больших скоростях. Увеличение массы материала до 1.0 кг еще более усугубляет тенденцию уменьшения длины стежка на больших скоростях, особенно при малых давлениях лапки. Сделан вывод, что для обеспечения наилучших условий продвижения материала в машине 1876 кл. необходимо устанавливать давление лапки »60 Н. Для обеспечения более строгого соблюдения диапазона изменения длины стежка при частоте вращения главного вала машины ³ 5000 мин-1 необходимо дальнейшее совершенствование конструкции механизма транспортирования.
В статье Ю.Ю.Щербаня и В.А.Горобца [84] выполнено экспериментальное определение зависимости величины посадки материала с различными физико-механическими свойствами при их стачивании от скорости главного вала швейной машины и усилия прижима прижимной лапки. Указывается, что необходимо учитывать возможность превышения допустимой величины посадки слоев материала при стабилизации длины стежка путем увеличения усилия прижима материала. Методика и методы оценки посадки, стягивания материала, прямолинейности строчки приведены в работе В.П.Полухина и Л.К.Милосердного [53].
В статьях Ю.Ю.Щербаня, В.А.Горобца, И.С.Силивончика [85],[86] исследуется возможность замены в механизме транспортирования рейки на рабочий орган с микрошероховатой поверхностью, получаемой напылением. Указано, что применение подобного рабочего органа позволяет увеличить в 1.5-2.0 раза коэффициент сцепления с материалами, уменьшить посадку, стягивание шва, стабилизировать длину стежка, а также снизить виброактивность машины.
В статье S.Mende [87] приведены результаты исследования взаимодействия системы “рейка - транспортируемый материал - прижимная лапка”. Отмечается, что на высоких скоростях (до 8000 мин-1) качество строчки во многом зависит от точности взаимодействия транспортирующих органов. Получены теоретические и экспериментальные зависимости влияния на прижимную лапку скорости шитья, траектории движения рейки, массы материала, жесткости пружины лапки.
1.3 Обзор алгоритмов подпрограмм кинематического анализа структурных групп Ассура, входящих в кинематические схемы транспортирующих механизмов.Механизмы транспортирования ткани швейных машин представляют собой рычажные механизмы достаточно сложной структуры. Для решения задач кинематического анализа подобных механизмов чаще всего используется ЭВМ, разрабатываются пакеты прикладных программ. Общих программ анализа кинематики рычажных механизмов произвольного вида не существует. Разработка таких программ является весьма сложной задачей, требующей от исследователя соответствующих математических моделей и алгоритмического обеспечения.
Настоящая глава посвящена обзору алгоритмического обеспечения решения задач кинематического анализа рычажных механизмов, применяемых для транспортирования ткани в швейных машинах. Для реечного транспортирующего механизма швейных машин на стадии кинематического анализа характерно решение следующих задач:
1) определение функций положения, первых и вторых передаточных функций обобщенных координат звеньев механизма от обобщенной координаты входного звена;
2) определение траектории движения заданных конструктором точек рабочего органа механизма – рейки;
3) определение величины шага транспортирования Т;
4) определение зависимости шага транспортирования Т от параметров регулирования длины стежка, предусмотренных кинематической схемой механизма;
5) нахождение предельных значений параметров регулирования соответствующих верхней и нижней границе изменения шага транспортирования.
Для дифференциальных транспортирующих механизмов, перемещение материала в которых происходит двумя зубчатыми рейками — основной и дополнительной, перечисленные задачи решаются для каждой рейки в отдельности и, кроме того, определяются: степень дифференцирования подачи m (отношение шага транспортирования дополнительной рейки к шагу транспортирования основной рейки); зависимость m от параметров регулирования, предусмотренных кинематической схемой механизма; граничные значения параметров регулирования.
В качестве аналитического метода описания математической модели для кинематического анализа таких сложных многозвенных рычажных механизмов, как реечные механизмы транспортирования ткани швейных машин, на наш взгляд наиболее применим метод погруппного анализа [4]. Суть его состоит в последовательном математическом описании структурных групп Ассура, входящих в состав механизма, в порядке их присоединения при образовании структурной схемы. Исходя из анализа структурных схем транспортирующих механизмов швейных машин, можно заключить, что в них, как правило, применяются двухповодковые структурные группы Ассура первой, второй и третьей модификаций, а также, различные модификации трехповодковых структурных групп. Алгоритм кинематического анализа реечного механизма транспортирования ткани, согласно методу погруппного анализа, представляет собой некоторый головной модуль, объединяющий отдельные модули, каждый из которых содержит алгоритм анализа соответствующей структурной группы Ассура, в порядке их присоединения друг к другу, начиная с входного звена.
Рассмотрим ниже математические модели и алгоритмы кинематического анализа структурных групп Ассура, наиболее часто встречающихся в схемах реечных механизмов транспортирования ткани швейных машин. При этом решение задачи кинематического анализа осуществляется на ЭВМ численно для ряда дискретных значений угла поворота a (обобщенной координаты) входного звена транспортирующего механизма. Дискретное значение угла a для i-го положения входного звена может быть, например, определено из выражения:
![]() , (1.1)
, (1.1)
где a0 – начальное значение угла a; Da - выбранный исследователем шаг изменения угла a; Nвр – коэффициент, характеризующий направление вращения: Nвр=+1 или –1 при вращении соответственно против или по часовой стрелке; N – количество рассчитываемых положений механизма (начальное положение механизма совпадает с нулевым), N=2p/Da. Величина a0 представляет собой исходное значение угла a, выбираемое конструктором произвольно.
1.3.1 Алгоритм кинематического анализа кривошипа.Кинематический анализ любого рычажного механизма начинается с анализа его входного звена. Задача кинематического анализа кривошипа (рис. 1.3.1) может быть сформулирована следующим образом.
Известны величины:
1) R – длина кривошипа O1A;
2) XO1, YO1 – координаты центра оси вращения кривошипа относительно произвольно заданной исследователем неподвижной системы координат OXY;
3) a - текущее значение угла поворота кривошипа, отстоящее от значения a0 на величиину Da;
4) Nвр – коэффициент, характеризующий направление вращения кривошипа (см. выше).
Требуется определить:
1) XA, YA – функции положения координат точки А кривошипа в неподвижной системе координат OXY по углу a;
2) ![]() - первую и вторую передаточные функции координат точки А по углу a в проекциях на оси OX и OY заданной неподвижной системы координат OXY.
- первую и вторую передаточные функции координат точки А по углу a в проекциях на оси OX и OY заданной неподвижной системы координат OXY.
Координаты XA, YA могут быть найдены из выражений:
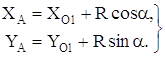 (1.2)
(1.2)
Дифференцируя по обобщенной координате a выражения (1.2) определим первую передаточную функцию координат XA, YA:
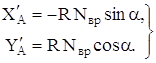 (1.3)
(1.3)
Дважды дифференцируя (1.2) по обобщенной координате a определим вторую передаточную функцию координат XA, YA:
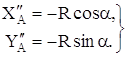 (1.4)
(1.4)
Блок-схема алгоритма кинематического анализа кривошипа представлена на рис. 1.3.2.
1.3.2 Алгоритм программы кинематического анализа звена механизма первого порядка.Задачу кинематического анализа звена механизма сформулируем следующим образом.
Известны величины (рис. 1.3.3):
1) ![]() – функции положения обобщенных координат, определяющих положение звена AB (m – номер звена в механизме) в неподвижной системе координат OXY (см. рис. 1.3.3) в зависимости от обобщенной координаты входного звена (кривошипа) a;
– функции положения обобщенных координат, определяющих положение звена AB (m – номер звена в механизме) в неподвижной системе координат OXY (см. рис. 1.3.3) в зависимости от обобщенной координаты входного звена (кривошипа) a;
2) ![]() - первые и вторые передаточные функции по обобщенной координате a;
- первые и вторые передаточные функции по обобщенной координате a;
3) ![]() - координаты некоторой точки К расположенной на звене AB в подвижной системе координат
- координаты некоторой точки К расположенной на звене AB в подвижной системе координат ![]() , неизменно связанной со звеном (см. рис 1.3.3).
, неизменно связанной со звеном (см. рис 1.3.3).
Требуется определить:
1) XK, YK – функции положения координаты точки К звена AB в заданной неподвижной системе координат OXY по координате a;
2) ![]() - первую и вторую передаточные функции координат точки K по обобщенной координате a.
- первую и вторую передаточные функции координат точки K по обобщенной координате a.
Пользуясь известными из аналитической механики соотношениями перехода из одной системы координат в другую, можем записать:
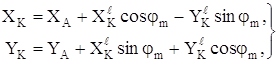 (1.5)
(1.5)
где ![]() ,
, ![]() ,
, ![]() .
.
Для определения первой передаточной функции координат XK, YK по a продифференцируем выражения (1.5) по обобщенной координате a:
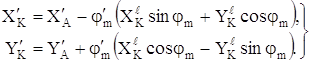 (1.6)
(1.6)
Здесь и ниже штрихом обозначена производная по обобщенной координате a.
Дважды дифференцируя по обобщенной координате a выражения (1.5), найдем вторую передаточную функцию координат XK, YK по a:
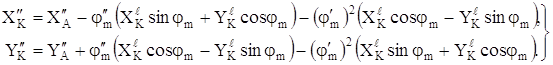 (1.7)
(1.7)
Здесь и ниже двумя штрихами обозначена вторая производная по обобщенной координате a.
Блок-схема алгоритма кинематического анализа звена представлена на рис. 1.3.4.
1.3.3 Алгоритм программы кинематического анализа двухповодковой структурной группы Ассура первой модификацииДвухповодковая структурная группа Ассура первой модификации (рис. 1.3.5) является одной из наиболее распространенных в плоских рычажных механизмах. Задачу анализа структурной группы первой модификации сформулируем следующим образом.
Известны величины (см. рис. 1.3.5):
1) L1, L2 – длины звеньев AD и BD соответственно;
2) XA, YA, XB, YB – функции положения координат шарниров A и B группы по a (см. выше) в заданной неподвижной системе координат OXY;
3) ![]() - первая передаточная функция координат шарниров A и B по обобщенной координате a в проекциях на оси неподвижной системы координат OXY;
- первая передаточная функция координат шарниров A и B по обобщенной координате a в проекциях на оси неподвижной системы координат OXY;
4) ![]() - вторая передаточная функция координат шарниров A и B по обобщенной координате a в проекциях на оси неподвижной системы координат OXY;
- вторая передаточная функция координат шарниров A и B по обобщенной координате a в проекциях на оси неподвижной системы координат OXY;
5) M – коэффициент, величина которого зависит от способа сборки, определяемого следующим образом (см. рис. 1.3.6,а): если поворот вектора ![]() вокруг точки B виден против часовой стрелки M=+1, иначе М=-1.
вокруг точки B виден против часовой стрелки M=+1, иначе М=-1.
Требуется определить:
1) j1 и j2 – функции положения угловых координат звеньев 1 и 2 группы по обобщенной координате a, отсчитываемые в положительном направлении (против часовой стрелки) от линии параллельной оси OX (AX1Y1 и BX2Y2 - подвижные системы координат неизменно связанные со звеньями 1 и 2 соответственно);
2) ![]() ,
,![]() - первую и вторую передаточные функции по обобщенной координате a угловых координат j1 и j2 звеньев группы.
- первую и вторую передаточные функции по обобщенной координате a угловых координат j1 и j2 звеньев группы.
Определим условия существования структурной группы при заданных параметрах, для чего найдем угол передачи m (см. рис. 1.3.5):
![]() , (1.8)
, (1.8)
где
![]() . (1.9)
. (1.9)
Учитывая, что ![]() и (1.8) получим неравенство:
и (1.8) получим неравенство:
![]()
Если ![]() , шарниры, A, B и D лежат на одной линии (см. рис. 1.3.6,б и 1.3.6,в). В этот момент в структурной группе происходит смена способа сборки, а также, как будет показано ниже, первая и вторая передаточные функции угловых координат звеньев j1 и j2 устремляются в бесконечность. Поэтому условие существования структурной группы запишем в следующем виде:
, шарниры, A, B и D лежат на одной линии (см. рис. 1.3.6,б и 1.3.6,в). В этот момент в структурной группе происходит смена способа сборки, а также, как будет показано ниже, первая и вторая передаточные функции угловых координат звеньев j1 и j2 устремляются в бесконечность. Поэтому условие существования структурной группы запишем в следующем виде:
![]() . (1.10)
. (1.10)
Блок-схема алгоритма кинематического анализа структурной группы первой модификации представлена на рис. 1.3.7. В блоке 4 производится проверка условий существования группы. Если условия (1.10) не выполняются (т.е. при заданных значениях исходных параметров происходит либо разрыв кинематической цепи, либо угол передачи принимает критическое значение), то дальнейший расчет (блоки 5‑14) прекращается (переход на блок 15). В блок‑схеме используются подпрограммы: решения уравнения вида :
![]() . (1.11)
. (1.11)
при вычислении sinj1 и cosj1 (см. блок 7); вычисления угловых координат в промежутке от 0 до 2p с учетом знака sin и cos (см. блоки 9, 10); решения систем двух линейных уравнений методом Крамера (см. блоки 12, 14).
1.3.4 Алгоритм программы кинематического анализа двухповодковой структурной группы Ассура второй модификацииДвухповодковая структурная группа Ассура второй модификации применяется в механизмах перемещения материала 876 класса и др. На рис. 1.3.8 структурная группа этой модификации представлена в наиболее общем виде. Задачу кинематического анализа структурной группы второй модификации сформулируем следующим образом.
Известны величины (см. рис. 1.3.8):
1) L1, L2 – длины звеньев 1 и 2 группы соответственно;
2) Q2 – угол между положительным направлением оси CX2 подвижной системы координат CX2Y2 (неизменно связанной с направляющей ползуна В и началом координат в точке С) и звеном BD группы;
3) XC, YC – функции положения координат какой-либо точки С, принадлежащей направляющей ползуна В, по углу a в системе координат OXY;
4) ![]() - первая и вторая передаточные функции по углу a координат XС, YС точки С в проекциях на оси OX и OY системы координат OXY;
- первая и вторая передаточные функции по углу a координат XС, YС точки С в проекциях на оси OX и OY системы координат OXY;
5) XA, YA – функции положения по углу a координат шарнира А (в заданной неподвижной системе координат OXY), присоединяющего структурную группу к другим структурным элементам кинематической схемы механизма одноподвижной вращательной кинематической парой;
6) ![]() - первая и вторая передаточные функции по углу a координат XA, YA шарнира А в проекциях на оси OX и OY;
- первая и вторая передаточные функции по углу a координат XA, YA шарнира А в проекциях на оси OX и OY;
7) j2 – функция положения угловой координаты направляющей ползуна В, отсчитываемая относительно оси параллельной оси OX в положительном направлении (против часовой стрелке) по углу a;
8) ![]() – первая и вторая передаточные функции угловой координаты j2 по углу a;
– первая и вторая передаточные функции угловой координаты j2 по углу a;
9) М1 – коэффициент, характеризующий способ сборки структурной группы определяемый следующим образом (рис. 1.3.9,а): если проекция вектора ![]() на ось СX2 системы координат CX2Y2 положительна, то способ сборки M1=+1, иначе М1=-1.
на ось СX2 системы координат CX2Y2 положительна, то способ сборки M1=+1, иначе М1=-1.
Требуется определить:
1) j1 – функцию положения угловой координаты звена AB группы по углу a;
2) ![]() – первую и вторую передаточную функции угловой координаты j1 по углу a;
– первую и вторую передаточную функции угловой координаты j1 по углу a;
3) XB, YB – функции положения координаты точки В ползуна 2 группы в системе координат OXY по углу a;
4) ![]() - первую и вторую передаточные функции по углу a координат XB, YB в проекциях на оси OX и OY системы координат OXY.
- первую и вторую передаточные функции по углу a координат XB, YB в проекциях на оси OX и OY системы координат OXY.
Блок-схема алгоритма кинематического анализа структурной группы второй модификации представлена на рис. 1.3.10. В блоке 6 происходит проверка условия существования группы. Если это условие не выполняется (т.е. при заданных значениях исходных параметров происходит разрыв кинематической цепи или угол давления принимает критическое значение) происходит переход на блок 18 и прекращение вычислительного процесса с выдачей предупреждающего сообщения о причине остановки вычислений. В блок-схеме используются подпрограммы: определения углов в промежутке от 0 до 2p с учетом знака sin и cos (см. блоки 4, 11); решения системы двух линейных уравнений методом Крамера (см. блоки 13, 16).
1.3.5 Алгоритм программы кинематического анализа двухповодковой структурной группы Ассура третей модификацииСтруктурная группа Ассура третей модификации применяется в механизмах перемещения материала 131-42+3 класса и др. На рис. 1.3.11 структурная группа этой модификации представлена в наиболее общем виде. Задачу кинематического анализа структурной группы третей модификации сформулируем следующим образом.
Известны величины (см. рис. 1.3.11):
1) L1 – длина плеча AC звена 1;
2) XQ1, YQ1 – функции положения координат точки Q1, принадлежащей направляющей ползуна В, по углу a в системе координат OXY;
3) ![]() - первая и вторая передаточные функции по углу a координат XС, YС точки Q1 в проекциях на оси OX и OY системы координат OXY;
- первая и вторая передаточные функции по углу a координат XС, YС точки Q1 в проекциях на оси OX и OY системы координат OXY;
4) XA, YA – функции положения по углу a координат шарнира А (в заданной неподвижной системе координат OXY), присоединяющего структурную группу к другим структурным элементам кинематической схемы механизма одноподвижной вращательной кинематической парой;
5) ![]() - первая и вторая передаточные функции по углу a координат XA, YA шарнира А в проекциях на оси OX и OY;
- первая и вторая передаточные функции по углу a координат XA, YA шарнира А в проекциях на оси OX и OY;
6) XB, YB – функции положения по углу a координат шарнира B (в заданной неподвижной системе координат OXY), присоединяющего структурную группу к другим структурным элементам кинематической схемы механизма одноподвижной вращательной кинематической парой;
7) ![]() - первая и вторая передаточные функции по углу a координат XB, YB шарнира B в проекциях на оси OX и OY;
- первая и вторая передаточные функции по углу a координат XB, YB шарнира B в проекциях на оси OX и OY;
8) j2 – функция положения угловой координаты направляющей ползуна В, отсчитываемая относительно оси параллельной оси OX в положительном направлении (против часовой стрелке) по углу a;
9) ![]() – первая и вторая передаточные функции угловой координаты j2 по углу a;
– первая и вторая передаточные функции угловой координаты j2 по углу a;
Требуется определить:
1) j1 – функцию положения угловой координаты шарнира А звена AС группы по углу a;
2) ![]() – первую и вторую передаточную функции угловой координаты j1 по углу a;
– первую и вторую передаточную функции угловой координаты j1 по углу a;
3) L2 – расстояние от шарнира B ползуна 3 группы до точки С.
4) ![]() - первая и вторая передаточные функции по углу a длины L2 в проекциях на оси OX и OY;
- первая и вторая передаточные функции по углу a длины L2 в проекциях на оси OX и OY;
5) XQ, YQ – функции положения координат точки Q, по углу a в системе координат OXY;
6) ![]() - первая и вторая передаточные функции по углу a координат XС, YС точки Q в проекциях на оси OX и OY системы координат OXY;
- первая и вторая передаточные функции по углу a координат XС, YС точки Q в проекциях на оси OX и OY системы координат OXY;
Блок-схема алгоритма кинематического анализа структурной группы второй модификации представлена на рис. 1.3.12.. В блок-схеме используются подпрограммы: определения углов в промежутке от 0 до 2p с учетом знака sin и cos (см. блок 7); решения системы двух линейных уравнений методом Крамера (см. блок 4).
1.3.6.Алгоритм программы определения величины шага транспортирования.В результате кинематического анализа механизма транспортирования ткани швейной машины на ЭВМ определяется ряд дискретных значений координат XQi и YQi, ![]() (i — номер положения входного звена механизма) среднего зуба Q рейки (в системе координат OXY), по которым может быть построена траектория движения среднего зуба Q и определена величина шага транспортирования. Задачу определения шага транспортирования сформулируем следующим образом:
(i — номер положения входного звена механизма) среднего зуба Q рейки (в системе координат OXY), по которым может быть построена траектория движения среднего зуба Q и определена величина шага транспортирования. Задачу определения шага транспортирования сформулируем следующим образом:
Известны величины:
1) Таблица значений координат XQi и YQi, ![]() ; среднего зуба Q рейки относительно заданной неподвижной системы координат OXY (определены на ЭВМ в результате кинематического анализа механизма транспортирования ткани).
; среднего зуба Q рейки относительно заданной неподвижной системы координат OXY (определены на ЭВМ в результате кинематического анализа механизма транспортирования ткани).
2) Высота H (см. рис. 1.3.11) уровня игольной пластины (задана конструктором).
Требуется определить величину шага транспортирования Т.
Под шагом транспортирования будем понимать величину Т (см. рис. 1.3.11) — расстояние между точками А и В, образованными пересечением линии игольной пластины Н—Н с траекторией движения среднего зуба рейки, т.е.:
![]() (1.12)
(1.12)
При движении рейки по траектории против часовой стрелки (см. рис. 1.3.11,а) сшиваемые материалы будут перемещаться в сторону от работающего (противоположную направлению оси OX), что соответствует прямой подаче. Вычисленное по формуле (1.12) значение шага транспортирования в этом случае будет положительно. В противном случае, при движении рейки по часовой стрелке (см. рис. 2.13,б) сшиваемые материалы будут перемещаться по направлению оси OX (в сторону на работающего), что соответствует обратной подаче. Вычисленное по формуле (1.12) значение шага транспортирования в этом случае будет отрицательно.
Для определения координаты XA точки А последовательно перебирая номера положения входного звена механизма i от 1 до N, найдем такое значение i=k0, при котором выполнялись бы следующие условия:
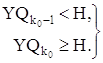 (1.13)
(1.13)
В том случае если ![]() (точка с координатами
(точка с координатами ![]() лежит на уровне игольной пластины), то
лежит на уровне игольной пластины), то ![]() . Если же
. Если же ![]() , то координата XA определяется, как координата пересечения прямой Y = Н и прямой проведенной через точки с координатами
, то координата XA определяется, как координата пересечения прямой Y = Н и прямой проведенной через точки с координатами ![]() и
и ![]() методом линейного интерполирования:
методом линейного интерполирования:
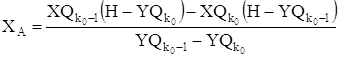 . (1.14)
. (1.14)
Аналогичным образом определяем координату XB точки B. Последовательно перебирая номера положения входного звена механизма i от 1 до N, найдем такое значение i=k1, при котором выполняются следующие условия:
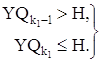 (1.15)
(1.15)
В том случае если ![]() (точка с координатами
(точка с координатами ![]() лежит на уровне игольной пластины), то
лежит на уровне игольной пластины), то ![]() . Если же
. Если же ![]() , то координата XB определяется как координата пересечения прямой Y = Н и прямой проведенной через точки с координатами
, то координата XB определяется как координата пересечения прямой Y = Н и прямой проведенной через точки с координатами ![]() и
и ![]() методом линейного интерполирования:
методом линейного интерполирования:
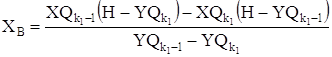 . (1.16)
. (1.16)
Блок-схема алгоритма определения шага транспортирования рейки представлена на рис. 1.3.12,а. Поиск точек А и В (см. рис. 1.3.12) пересечения траектории движения рейки с игольной пластиной происходит по одинаковой схеме. Различны только условия поиска: для момента выхода рейки над игольной пластиной это условие (1.13) - поиск точки А; для момента ухода рейки под игольную пластину это условие (1.15) - поиск точки В. Поэтому, алгоритм поиска координаты X точки пересечения целесообразно выделить в отдельную подпрограмму (см. блоки 2 и 3, рис. 1.3.12,а). Блок‑схема подпрограммы поиска точки пересечения траектории движения рейки с игольной пластиной представлена на рис. 1.3.12,б. В этой подпрограмме организован цикл по параметру i (номеру положения входного звена механизма) от 1 до N. В зависимости от того поиск какой точки задан в блоке 3 проверяется условие (1.13) — для точки А, или (1.15) — для точки B. Если найден номер i удовлетворяющий условию блока 3, то этот номер запоминается (блок 4) в переменной k. Далее в блоке 6 определяется лежит ли точка с координатами XQk, YQk на игольной пластине, если условие блока 6 выполняется то подпрограмма возвращает координату X найденной точки, в противном случае координата X точки пересечения траектории среднего зуба рейки с игольной пластиной определяется интерполированием по формулам (1.14) или (1.16) в зависимости от условий поиска поставленных в блоке 3. Заметим, что формулы (1.14) и (1.16) отличаются только номером найденного положения входного звена механизма k0 либо k1. Если в цикле (блоки 2—3) не найден номер i, удовлетворяющий условию поиска блока 3, то в блоке 5 фиксируется отсутствие пересечения траектории движения среднего зуба рейки с игольной пластиной.
1.3.7 Алгоритм головного модуля программы, объединяющего в себе описанные подпрограммы в единую программу кинематического анализа.Выше были разработаны алгоритмы и программное обеспечение для кинематического анализа отдельных структурных групп Ассура, входящих в состав реечных механизмов транспортирования ткани. Как правило, в этих механизмах можно выделить узлы:
- горизонтальных перемещений рейки;
- вертикальных перемещений рейки;
- рейки.
Каждый из этих узлов может быть представлен в виде кинематической цепи, состоящей из одной и более структурных групп Ассура, соединенных между собой последовательно.
Чтобы произвести кинематический анализ произвольного реечного транспортирующего механизма на ЭВМ с использованием разработанных выше подпрограмм кинематического анализа отдельных структурных групп Ассура, необходимо объединить указанные подпрограммы в единой программе – головном модуле. Головной модуль должен выполнять следующие задачи: ввод необходимых для кинематического анализа механизма исходных данных, кинематический анализ механизма, вывод результатов счета. Исходными данными для кинематического анализа механизма являются его структурная схема, геометрические размеры звеньев и координаты неподвижных опор. Кинематический анализ производится головным модулем путем вызова на выполнение подпрограмм анализа отдельных структурных групп Ассура в установленной пользователем согласно структурной схеме анализируемого механизма последовательности. Вывод данных, полученных в результате анализа, как правило, удобнее всего производить в форме таблиц и графиков.
Основной и наиболее ответственной частью головного модуля является непосредственно кинематический анализ механизма. Для разработки указанного алгоритма необходимо установить последовательность кинематического анализа групп Ассура, входящих в структурную схему транспортирующего механизма. Алгоритм кинематического анализа всего механизма, можно составить путем последовательного анализа кинематических цепей узлов: горизонтальных перемещений, вертикальных перемещений, узла рейки. Структура такого алгоритма представлена на рис. 1.3.13. Согласно данному алгоритму кинематический анализ каждой из указанных кинематических цепей узла должен представлять собой последовательный анализ отдельных структурных групп Ассура, входящих в эту цепь, в порядке их присоединения друг к другу.
Для обеспечения понимания структуры головного модуля алгоритма кинематического анализа реечного транспортирующего механизма рассмотрим его на конкретном примере. Рассмотрим алгоритм кинематического анализа механизма транспортирования ткани швейной машины 2222 кл. (см. рис. 1.3.14). На основании анализа структурной схемы этого механизма в нем можно выделить кинематические цепи узлов: подачи - O1ABO2, подъема – O1DEO3 и рейки (рычаг CF и ползун F). Разобьем указанные кинематические цепи на структурные группы Ассура. Кинематическая цепь узла подачи (O1ABO2) состоит из кривошипа O1A с присоединенной к нему структурной группой первой модификации ABO2. Кинематическая цепь узла подъема (O1DEO3) состоит из кривошипа O1D с присоединенной к нему структурной группой первой модификации DEO3. Узел рейки представляет собой структурную группу третьей модификации (шатун CF и ползун F). Согласно описанной выше общей структуре, блок-схема алгоритма кинематического анализа рассматриваемого механизма транспортирования может иметь вид, представленный на рис. 1.3.15. Данный алгоритм предполагает использование подпрограмм кинематического анализа: кривошипа (блоки 4, 7), структурной группы первой модификации (блоки 5, 8), звена (блоки 6, 9, 11), структурной группы третьей модификации (Алгоритм анализа структурной группы третьей модификации может быть составлен по аналогии с алгоритмами анализа структурных групп первой или второй модификаций) (блок 10), определения шага транспортирования (блок 12).
Аналогичным образом может быть построен алгоритм головного модуля программы кинематического анализа других механизмов транспортирования, имеющих схожую структуру. Однако ряд механизмов транспортирования ткани в составе узла горизонтальных перемещений рейки содержат узел регулирования шага транспортирования, позволяющий изменять направление подачи материала на ходу машины. При составлении алгоритма кинематического анализа подобных механизмов целесообразно узел регулирования шага транспортирования рассматривать как отдельную кинематическую цепь.
Рассмотрим, например, механизм транспортирования ткани швейной машины 1022 кл. (см. рис. 1.3.16). Структура узлов вертикальных перемещений и рейки в данном механизме аналогична рассмотренному выше механизму 2222 кл. Однако в рассматриваемом механизме предусмотрен узел регулирования шага транспортирования и направления подачи. Выделим узел регулирования в отдельную кинематическую цепь. Тогда узел горизонтальных перемещений рейки можно представить в виде кинематической цепи состоящей из кривошипа O1A с последовательно присоединенными к нему двумя структурными группами первой модификации ABG и BLO2. Узел регулирования шага транспортирования может быть представлен в виде кинематической цепи состоящей из рычага-регулятора O5P с присоединенной к нему в шарнире H структурной группой первой модификации HGO4. Блок-схема алгоритма кинематического анализа данного механизма может иметь вид, представленный на рис. 1.3.17. Данный алгоритм предполагает использование подпрограмм кинематического анализа: кривошипа (блоки 6, 10), структурной группы первой модификации (блоки 5, 7, 8, 11), третьей модификации (блок 13), анализа звена (блоки 9, 12, 14), определения шага транспортирования (блок 15). С необходимыми поправками на тип структурных групп рассмотренный алгоритм может быть использован при разработке головного модуля программ кинематического анализа других транспортирующих механизмов со схожей структурой, например, механизмов транспортирования швейных машин 97 кл.
Последовательность кинематического анализа узлов горизонтальных и вертикальных перемещений рейки при анализе механизмов рассмотренных типов не имеет значения, т.е. можно произвести сначала кинематический анализ узла горизонтальных перемещений рейки, потом узла вертикальных перемещений, а можно и наоборот. Анализ же кинематической цепи узла рейки не может быть произведен без анализа узлов горизонтальных и вертикальных перемещений. Если в транспортирующем механизме рейка располагается непосредственно на узле вертикальных перемещений последовательность анализа узлов вертикальных и горизонтальных перемещений имеет существенное значение.
Например, в механизме транспортирования ткани швейной машины 66 кл. (см. рис. 1.3.20) кинематическая цепь узла горизонтальных перемещений рейки состоит из кривошипа O1A и присоединенной к нему структурной группой первой модификации ABO2. Узел вертикальных перемещений рейки может быть представлен в виде кинематической цепи, состоящей из кривошипа O3D и структурной группы первой модификации DEC, причем на звене EC этой группы расположена рейка Q. Последовательность кинематического анализа данного механизма должна быть такой. Вначале производится анализ кинематической цепи узла горизонтальных перемещений. Затем анализ кинематической цепи узла вертикальных перемещений. Указанная последовательность объясняется тем, что для проведения кинематического анализа узла вертикальных перемещений рейки необходимо знать функцию положения, первую и вторую передаточные функции координат шарнира C структурной группы DEC, которые не могут быть определены без предварительного анализа узла горизонтальных перемещений. Блок-схема алгоритма кинематического анализа рассматриваемого механизма представлена на рис. 1.3.21. Данный алгоритм предполагает использование подпрограмм кинематического анализа: кривошипа (блоки 4, 7), структурной группы первой модификации (блоки 5, 8), анализа звена (блоки 6, 9), определения шага транспортирования (блок 11).
Дифференциальные реечные механизмы транспортирования ткани характеризуются тем, что привод основной и дополнительной реек осуществляется разными кинематическими цепями. При составлении алгоритма кинематического анализа указанных механизмов возможны два способа. Первый способ состоит в том, чтобы дифференциальный механизм транспортирования ткани условно разбить на два механизма транспортирования соответственно основной и дополнительной реек. В каждом из этих механизмов можно выделить узлы горизонтальных, вертикальных перемещений, рейки, регулирования шага транспортирования. По аналогии с рассмотренными выше алгоритмами анализа однореечных механизмов в этом случае следует составить два алгоритма кинематического анализа механизмов транспортирования соответственно основной и дополнительной реек. Рассмотренный способ можно применить, например, для составления алгоритма кинематического анализа механизма транспортирования ткани швейной машины 208 кл. (см. рис. 1.3.20). Данный механизм транспортирования может быть разбит на механизмы транспортирования: основной (см. рис. 1.3.20,а) и дополнительной реек (см. рис. 1.3.20,б). Разбивая указанные механизмы на кинематические цепи, отметим, что привод вала подачи O2 в рассматриваемом механизме одинаков как для основной, так и для дополнительной реек и может быть представлен в виде кинематической цепи состоящей из кривошипа O1A и структурной группы первой модификации ABO2. Алгоритм анализа всего дифференциального транспортирующего механизма представлен на рис. 1.3.21. Данный алгоритм предполагает использование подпрограмм кинематического анализа: кривошипа (блок 4), структурной группы первой модификации (блок 5), анализа звена (блоки 6, 8, 12), структурной группы второй модификации (блок 10), трехповодковой структурной группы (блоки 7, 11), определения шага транспортирования Т1 и Т2 соответственно основной Q и дополнительной N реек (блоки 13, 14). Вычисления по данному алгоритму завершаются определением степени дифференцирования подачи m=Т2/Т1 (см. блок 15).
Второй способ составления алгоритма кинематического анализа дифференциальных реечных механизмов транспортирования наиболее применим для механизмов, в которых рычаг дополнительной рейки совершает движения в направляющих основной рейки (см. механизм транспортирования на рис. 1.3.22,). В подобных механизмах привод вертикальных перемещений основной и дополнительной реек, как правило, одинаков. При составлении алгоритма кинематического анализа из состава всего дифференциального механизма необходимо выделить механизм основной рейки. Разбив выделенный механизм на кинематические цепи привода горизонтальных и вертикальных перемещений, составить алгоритм его кинематического анализа. После этого выделить кинематическую цепь привода дополнительной рейки и добавить алгоритм кинематического анализа этой цепи к алгоритму кинематического анализа механизма основной рейки. Составленный таким образом алгоритм кинематического анализа дифференциального механизма транспортирования ткани швейной машины 876 кл. представлен на рис.1.3.23. В рассматриваемом механизме привод основной рейки Q (см. рис. 1.3.22) может быть разбит на кинематическую цепь горизонтальных перемещений (кривошип O1D и структурная группа первой модификации DEO2) и кинематическую цепь вертикальных перемещений (кривошип O1A и структурная группа первой модификации ABC). Кинематическая цепь дополнительной рейки N может быть представлена в виде двух последовательно присоединенных структурных групп второй модификации LF и FKM. Положение шарнира L структурной группы LF определяется углом наклона b рычага O3S регулирования степени дифференцирования подачи m. Алгоритм кинематического анализа данного механизма (см. рис. 1.3.23) предполагает использование подпрограмм кинематического анализа: кривошипа (блок 4), структурной группы первой модификации (блоки 5, 7), анализа звена (блоки 6, 8, 12), структурной группы второй модификации (блоки 10, 11), определения шага транспортирования Т1 и Т2 соответственно основной Q и дополнительной N реек (блоки 13, 14). В конце счета определяется степень дифференцирования подачи m (см. блок 15).
2. Алгоритм исследования кинематики нижней рейки машины 131-42+3 класса 2.1 Конструкционная схема механизма транспортирования ткани машины 131-42+3 класса
Машины этого ряда предназначены для выполнения стачивающих операций однолинейной строчкой, образованной стежками типа 301, при изготовлении одежды из легких, средних и среднетяжелых тканей. Разработчик и изготовитель машин — завод «Легмаш» (г. Орша) производственного объединения «Промшвеймаш».
В состав ряда входят неавтоматизированные и автоматизированные швейные машины с различными механизмами продвижения материала общего назначения, а также специализированные машины, имеющие различную технологическую оснастку.
Перспективный ряд, разработанный ВНИИЛтекмаш, ЦНИИШП и объединением «Промшвеймаш», насчитывает более семидесяти классов машин. В настоящее время разработаны и рекомендованы к серийному производству тридцать классов машин. В основу ряда положен блочно-модульный принцип создания машин.
В машинах ряда используются четыре унифицированные между собой швейные головки, отличающиеся способом и, соответственно, механизмом продвижения материала: одной нижней рейкой, двумя нижними рейками (горизонтальный дифференциал) , нижней рейкой и отклоняющейся иглой, нижней и верхней рейками (вертикальный дифференциал). Машины в зависимости от толщины прошиваемых материалов (3; 5 и 7 мм) имеют модификации, отличающиеся высотой подъема прижимной лапки (6; 8 и 10 мм) и ходом иглы (29; 32 и 35 мм), а также толщиной (номерами) применяемых игл (№ 75—90, 100—11О и 120—150 соответственно). Некоторые машины имеют встроенный механизм обрезки материала.
Неавтоматизированные машины оснащаются традиционным фрикционным приводом, поэтому оператор в процессе работы затрачивает много времени и усилий на выполнение таких операций, как повернуть шкив машины до нужного положения иглы (верхнего — при укладывании и съеме изделия, нижнего — при повороте изделия для выполнения строчки сложной конфигурации); поднять и опустить лапку, обрезать нитки; выполнить закрепку в начале и конце строчки. Кроме того, при выполнении технологической операции и в процессе ее освоения требуется различная скорость работы машины.
При мелкосерийном производстве этих операций немного, при массовом же производстве они становятся монотонными и в значительной мере утомляют оператора. Поэтому в рамках этого ряда разработано уже пятнадцать классов автоматизированных машин, обеспечивающих автоматическое выполнение некоторых операций (останов иглы в заданном, верхнем или нижнем, положении; подъем и опускание лапки; обрезка игольной и челночной ниток; устойчивая работа машины на нескольких скоростях; выполнение закрепки в начале и конце строчки). Предусмотрено два варранта исполнения машин: без закрепки и с закрепкой в начале и конце строчки.
Использование средств автоматизации позволяет поднять производительность труда на операции от 10 до 25% (в зависимости от ее содержания) и значительно улучшить условия труда. Дальнейшее развитие машин этого ряда пойдет по пути создания различных сочетаний модулей (швейной головки и средств автоматизации) и технологической оснастки.
Создание широкой номенклатуры оборудования требует его четкой классификации и обозначения. Существующее обозначение швейного оборудования, как правило, не несет смысловой информации, а представляет собой цифры (класс), отражающие хронологию выпуска машин.
Для машин этого ряда использованы обозначения в соответствии со смысловой классификацией. Основой классификации является назначение оборудования, которое для швейных машин определяется классом выполняемого стежка. По международной классификации все стежки делятся на шесть классов: 100—однониточные цепные; 200—ручные и им аналогичные; 300 — челночные; 400 — цепные двухниточные; 500 _ обметочные; 600 — плоские.
Обозначение оборудования строится по иерархическому принципу и включает в себя обозначения ряда, модификации, средств автоматизации, технологической и организационной оснастки Так как организационная оснастка сейчас находится в стадии разработки и ей еще не установлены обозначения, обозначения машин применительно к рассматриваемому ряду состоят из четырех групп:
Х1 Х2 X3—X4 X5 X6 + У + Z.
Первая группа обозначает ряд машины и состоит из трех разрядов:
первый (Х1) определяет последовательность совершенствования или развития ряда; второй (Х2) —класс стежка; третий (Хз) — особенности данного ряда (например, расположение оси челнока, особенности обрабатываемого материала, скоростные возможности машин и т. п.).
Вторая группа характеризует конкретную машину (модификацию)ряда: разряд X4 показывает способ или тип продвижения материала в машине; разряд Х5, характеризует толщину пакета обрабатываемого материала; разряд Х6 указывает на наличие встроенных дополнительных устройств, расширяющих технологические возможности машин. Разряд Х6 для машин челночного стежка не используется, он предназначен для машин цепного и стачивающе-обметочного стежков.
Третья группа (У) обозначает комплект средств автоматизации, а четвертая (Z) — комплект технологической оснастки, специализирующей машину на выполнение конкретной операции.
Для КУР-31 разряды принимают следующие значения:
X1=0 (исходный ряд—не ставится, по мере совершенствования ряда может иметь последовательные значения 1, 2, 3,...);
Х2=3 (машины челночного стежка);
Х3=1 (первый конструктивный ряд машин одноигольных челночного стежка, имеющих горизонтальную ось вращения челнока и предназначенных для пошива легких, средних и средне-тяжелых материалов, максимальная частота вращения главного вала до 6000 об. в мин.1);
Х4=1, 2, 3, 4 (продвижение материала соответственно одной нижней рейкой, двумя нижними рейками, рейкой и иглой, нижней и верхней рейками);
Х5=1, 2, 3 (толщина обрабатываемого пакета до 3; 5 и 7 мм);
Х6=1 (наличие механизма ножей для обрезки края материала);
У = 1 ... 299 (1...49—отсутствие средств автоматизация, фрикционный привод; 50 ...99 — автоматический останов машины в заданном положении, подъем и опускание лапки и обрезка ниток; 100 ,..149—то же, что и 50... 99, и автоматическое выполнение закрепки в начале и конце строчки; свыше 150—то же, что и 100 ...149, и программное выполнение сложной строчки; при обозначениях наборов более 50 на машинах устанавливается регулируемый привод);
Z=300 ...699 (301 — изготовление отделочных складок на мужских сорочках, 302 — обработка пояса женского плаща, 303—притачивание манжет к рукавам мужской сорочки).
Для продвижения труднотранспортируемых материалов, в первую очередь с малым коэффициентом трения, требуется более четкая фиксация их слоев в процессе продвижения. Для пошива таких материалов используются машины (классы 31-41+3, 31-42+3, 31-43+3), в которых материал в процессе продвижения зажимается между нижней и верхней рейками (вертикальный дифференциал).
Нижняя рейка Q2 (рис.2.1) получает движение по эллипсообразной траектории от механизма традиционной структуры, используемого в базовой машине. На распределительном валу О2, получающего вращение от главного вала О7 с помощью зубчато-ременной передачи, установлены два эксцентрика — 27 и 28. От эксцентрика 27 с помощью звеньев 23, 24, 25 и 26 сообщаются колебательные движения коромыслу 21, а следовательно, и валу О5 продвижения. Коромысло 22 передает эти движения державке 33, обеспечивая горизонтальные перемещения рейке Q2 на длину стежка, которая зависит от положения подвижной опоры O6. Эксцентрик 28 с помощью звеньев 29,30,31,32 и вала O8 обеспечивает перемещение рейки Q2 по вертикали.
Верхняя рейка Q1 также движется по эллипсообразной траектории. Движения по горизонтали нижней Q2 и верхней Q1 реек должны быть синхронными. Это обеспечивается тем, что кинематическая цепь горизонтального перемещения верхней рейки Q1 получает движение от вала О5 продвижения нижней рейки Q2. На валу О5 установлено коромысло 21, которое с помощью звеньев 20, 19, 18, 17, 11 и валов O4 и О3 обеспечивает горизонтальные перемещения державке 9 с закрепленной на ней рейкой Q1.
Державка 9 с одной стороны шарнирно связана с подвеской 6, а с другой имеет кронштейн 4, передающий движение с помощью ползуна 7 и кулисы 8 на горизонтальное плечо рычага 5. Подвеска 6 шарнирно соединена с кронштейном 3 штанги 2, несущей на себе лапку 38.
Вертикальное плечо рычага 5 через кулисное звено 13, а также через звенья 12, 14, 15 и ось O1 связано с установленным на главном валу О2 эксцентриком 16. Таким образом, за один оборот главного вала О7 рычаг 5 совершает возвратное движение по вертикали. Пружина 35 обеспечивает прижатие к материалу соответственно верхней рейки Q1 или лапки 38.
При работе такого механизма могут иметь место два режима продвижения материала. При пошиве тонких материалов лапка 38 постоянно прижимает материал к игольной пластине P (см. рис. 2.2), а рейки Q1 и Q2 при их сближении имеют между собой зазор, величина которого достаточна для надежного захвата материала М и перемещения его относительно лапки.
При пошиве толстых, а особенно рыхлых материалов, необходима более четкая фиксация материала. Для этого траекторию верхней рейки Q1 (см. штрихпунктирные линии) опускают ниже игольной пластины P. Тогда после соприкосновения рейки Q1 с материалом рычаг 5 (см. рис 2.1), продолжая поворот по часовой стрелке, поднимает через кронштейн 3 штангу 1 и закрепленную на ней лапку 38. Продвижение материала М (см. рис. 2.2) производится рейками Q1 и Q2 при поднятой лапке Л. При подъеме рейки Q1 лапка Л опускается на материал и фиксирует его на игольной пластине. Такой режим в производственном обиходе называется «переплясом».
Конструктивно механизм верхней рейки выполнен путем установки дополнительных звеньев как внутри рукава машины, так и на его тыльной стороне. В рукаве машины дополнительно установлены валы 14 (рис. 2.3) и 23, а на приливах тыльной стороны рукава машины — оси 7 и 8. На штанге 50 винтом 49 закреплена лапка 46. Сквозь штангу пропущен шток 11, через палец 2 опирающийся на державку 51. На державке закреплена верхняя рейка 47, взаимодействующая при продвижении материала с нижней рейкой 48. Державка 51 подвеской 52 шарнирно соединена с кронштейном штанги 50. На штангу 50 сверху действует пластинчатая пружина 20, а на шток 11 — аналогичная пружина 15.
Для перемещения державки 51 с верхней рейкой 47 по горизонтали предусмотрен специальный механизм, аналогичный
механизму горизонтального перемещения нижней рейки 48. На распределительном валу 41 установлен эксцентрик 39, от которого с помощью шатуна 40 и звена 42 регулятора сообщаются колебательные движения коромыслу 43 и валу 54, расположенному внутри вала продвижения 53. Коромысло 43 шатуном 38 связано с коромыслом 24, закрепленным с помощью клеммы на валу 14. На передней части вала также клеммой закреплено коромысло 13 через тягу 12, сообщающее колебательные движения оси 8 коромыслу 4. От коромысла 4 через звено 1 получает движение по горизонтали державка 51 с верхней рейкой 47.
На главном валу 21 установлен эксцентрик 17, который с помощью шатуна 19, коромысла 22, вала 23, коромысла 10, шатуна 9, оси 7, коромысла 6 и шатуна 5 сообщает колебательные движения угловому рычагу 3, горизонтальное плечо которого поднимает и опускает державку 51 с верхней рейкой 47. Таким образом, верхняя рейка 47 совершает движение по эллипсообразной траектории.
Стойки 45 и 44 механизмов регулировки горизонтального перемещения нижней 48 и верхней 47 реек установлены на телескопических (друг в друге) валах. На правых концах валов установлены коромысла 36 и 34, связанные через тяги 33 и 32 с рычагами регулятора длины стежка. Установленные на коромыслах ролики 35 и 37 опираются на толкатели, установленные под крышкой стола машины.
Величины перемещения нижней и верхней реек могут регулироваться независимо с помощью гаек 30, 29 и шкалы 28. Нажимом на рукоятку 27 обеспечивается реверс. Нижнее крайнее положение рукоятки 27 обеспечивается упором 31, устанавливаемым рамкой 25 с помощью гайки 26.
Регулировка усилия зажатия материала между рейками в процессе продвижения обеспечивается винтом 16, а усилие прижатия материала к игольной пластине винтом 18.
Похожие работы
... исполнительных органов. Кинематическая схема может быть плоской или пространственной (в ортогональном или аксонометрическом изображении). На рис. I представлена плоская кинематическая схема механизмов иглы и нитепритягивателя универсальной швейной машины 1022 класса. На рис. 2 - пространственная конструктивно-кинематическая схема. Машина 1022 класса предназначена для стачивания деталей ...
... нарушаются элементарные дидактические требования, преобладает пассивное восприятие учебной информации учащимися, нерационально тратится учебное время. Глава 2. Методика использования аудиовизуальных и технических средств обучения при изучении раздела «Технология обработки ткани 5 класс» 2.1 Комплексно-методическое обеспечение раздела 1. Учебно-методическая документация № п/п Наименование ...
... , расстоянием между иглами и др. Общая классификация рядов приведена в таблице 5. Таблица 5 Классификация рядов машин МО-6 3. Основные принципы совершенствования швейных машин За последние несколько десятилетий специалисты, работающие в химической промышленности, металлургии, предложили практическому машиностроению большое количество новых полимерных и композитных материалов, новых ...
... , хранении, употреблении, к огне- и взрывоопасное, к срокам периодического осмотра, контроля, переконсервации и т.п. ЛЕКЦИЯ 4 План лекции: 4.1. Организация процесса проектирования-конструирования и освоения технологического оборудования 4.2. Стадии и этапы разработки конструкторской документации 4.1. Организация процесса проектирования-конструирования и освоения технологического ...
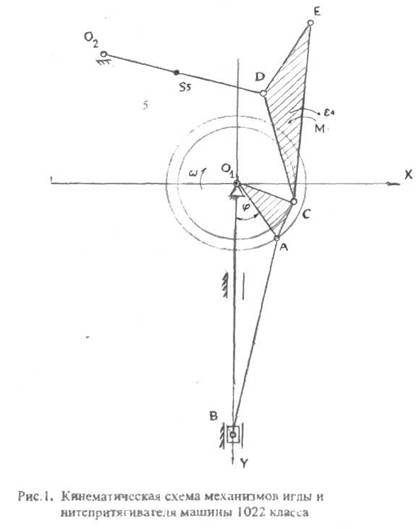
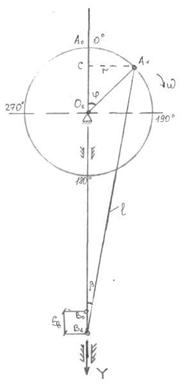
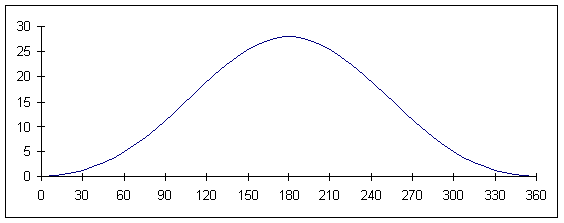
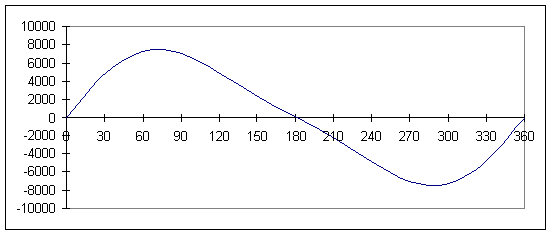
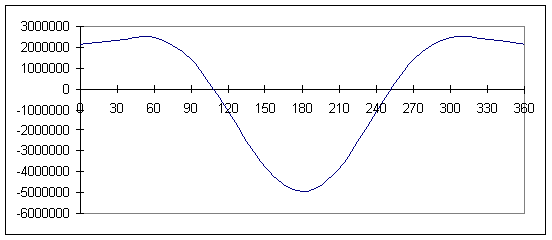


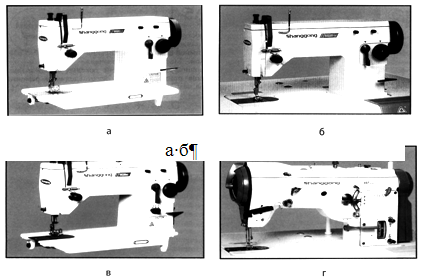


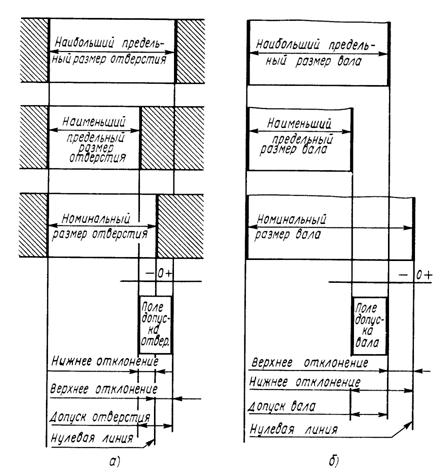
0 комментариев