Описание алгоритма

3 Описание алгоритма

Были разработаны следующие функции (текст программы приведен в приложении 1).

Функция smezver (x y snaid snov) – определяет, является ли вершина y смежной с одной из новых вершин (x – входит в список новых вершин, y – не входит в списки новых и найденных вершин).

Параметры:

- x - первая вершина ребра;

- y - вторая вершина ребра;

- snaid - список найденных вершин;

- snov - список новых вершин.

Функция smez (snaid snov sreb) - поиск смежных с новыми вершинами вершин.

Параметры:

- snaid - список найденных вершин;

- snov - список новых вершин;

- sreb - список ребер.

Функция shir(snaid snov y sreb) - поиск в ширину пути.

Параметры:

- snaid - список найденных вершин;

- snov - список новых найденных вершин;

- y - вершина для поиска;

- sreb - список ребер.

Функция path(x y sreb) – поиск пути от вершины x к вершине y.

Параметры:

- x - первая вершина;

- y - вторая вершина;

- sreb - список ребер.

Функция perebor(fver sver sreb) - перебор вершин и поиск пути от первой вершины ко всем остальным.

Параметры:

- fver - первая вершина;

- sver - список вершин:

- sreb - список ребер.

Функция svgraf(sver sreb) - определение связанности графа.

Параметры:

- sver - список вершин;

- sreb - список ребер.

4 Обоснование набора тестов

При тестировании используются следующие тесты:

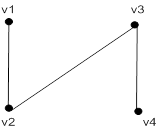
Рис.4.1 – Тест 1. Связанный граф

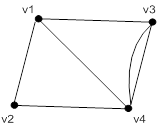
Рис. 4.2 – Тест 2. Связанный граф

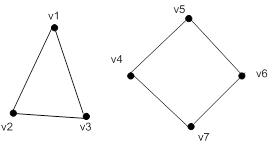
Рис. 4.3 – Тест 3. Несвязанный граф

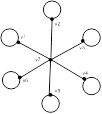
Рис. 4.4 – Тест 4. Связанный граф

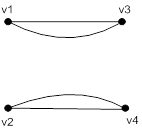
Рис. 4.5 – Тест 5. Несвязанный граф

Рис. 4.6 – Тест 6. Связанный граф

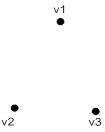
Рис. 4.7 – Тест 7. Несвязанный граф

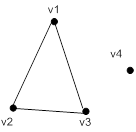
Рис. 4.8 – Тест 8. Несвязанный граф

Перечисленные тесты представляют собой различные входные данные, которые позволяют полностью проверить работу программы.

При тестировании все тесты были выполнены успешно. Результаты работы программы приведены в приложении 2.

ЗАКЛЮЧЕНИЕ

В данной работе написана программа на XLisp, определяющей, является ли данный неориентированный граф связным.

Все поставленные цели выполнены: приобретены навыки и методы программирования достаточно сложных задач на языках логического программирования, а также проведена подготовка к выполнению дипломного проекта.

Программа отлажена и протестирована.

СПИСОК ЛИТЕРАТУРЫ

1 Лутай В.Н. Программирование на языках Лисп и Пролог. ТРТУ,1998.

2 Филд А., Харрисон П. Функциональное программирование. - М.: Мир, 1993.

3 Уилсон Р. Введение в теоpию гpафов. - М.: Миp, 1977.

ПРИЛОЖЕНИЕ 1

 

Текст программы

; смежная вершина (первая вершина ребра, вторая вершина ребра,

; список найденных вершин, список новых вершин)

(defun smezver(x y snaid snov)

(cond

((not (member x snov)) nil) ;x не является новой вершиной

((member y snov) nil) ;y является новой вершиной

((member y snaid) nil) ;y является ранее найденной вершиной

(t t))) ;вершина является новой смежной вершиной

;поиск смежных вершин (список найденных вершин, список новых вершин, список ребер)

(defun smez(snaid snov sreb)

(cond

((null sreb) nil) ;конец поиска

((smezver (caar sreb) (cadar sreb) snaid snov) ;смежная вершина

(cons (cadar sreb) (smez snaid snov (cdr sreb)))) ;добавление в список

((smezver (cadar sreb) (caar sreb) snaid snov) ;смежная вершина

(cons (caar sreb) (smez snaid snov (cdr sreb)))) ;добавление в список

(t (smez snaid snov (cdr sreb))))) ;пропуск ребра

;поиск в ширину (список найденных вершин, список новых найденных вершин,

; вершина для поиска, список ребер)

(defun shir(snaid snov y sreb)

(cond

 ((null snov) nil) ;не найдено ни одной новой вершины

 ((member y snov) t) ;вершина найдена

 (t (shir (append snaid snov) (smez snaid snov sreb) y sreb)))) ;добавление новых вершин

;поиск пути (первая вершина, вторая вершина, список ребер)

(defun path(x y sreb)

(shir nil (list x) y sreb)) ;поиск в ширину

;перебор вершин (первая вершина, список вершин, список ребер)

(defun perebor(fver sver sreb)

(cond

 ((null sver) t) ;конец перебора

 ((path fver (car sver) sreb) (perebor fver (cdr sver) sreb)) ;путь найден

 (t nil))) ;нет пути

;определение связанности графа(список вершин, список ребер)

(defun svgraf(sver sreb)

 (perebor (car sver) (cdr sver) sreb)) ;перебор вершин и поиск пути от первой вершины ко всем остальным

ПРИЛОЖЕНИЕ 2

 

Результаты работы программы

Тест: 1

Выражение: (svgraf '(v1 v2 v3 v4) '((v1 v2) (v2 v3) (v3 v4)))

Результат: Т

Тест: 2

Выражение: (svgraf '(v1 v2 v3 v4) '((v1 v2) (v2 v4) (v2 v3) (v3 v4) (v1 v4) (v3 v4)))

Результат: T

Тест: 3

Выражение: (svgraf '(v1 v2 v3 v4 v5 v6 v7) '((v1 v2)(v2 v3)(v1 v3)(v4 v5)(v4 v7)(v5 v6)(v6 v7)))

Результат: NIL

Тест: 4

Выражение: (svgraf '(v1 v2 v3 v4 v5 v6) '((v1 v7)(v2 v7)(v3 v7)(v4 v7)(v5 v7)(v6 v7)(v1 v1)(v2 v2)(v3 v3)(v4 v4)(v5 v5)(v6 v6)))

Результат: T

Тест: 5

Выражение: (svgraf '(v1 v2 v3 v4) '((v1 v2)(v1 v2)(v3 v4)(v3 v4)))

Результат: NIL

Тест: 6

Выражение: (svgraf '(v1) nil)

Результат: T

Тест: 7

Выражение: (svgraf '(v1 v2 v3) nil)

Результат: NIL

Тест: 8

Выражение: (svgraf '(v1 v2 v3 v4) '((v1 v2) (v2 v3) (v3 v1)))

Результат: NIL