Зная количество деталей для каждого их вида, составляющих рациональный раскрой, формируется искомый вектор х

6. Зная количество деталей для каждого их вида, составляющих рациональный раскрой, формируется искомый вектор х.

//процедура вычисления рационального раскроя

procedure searchRationalCut(

materialLength: integer;

detailAmount: integer;

var details: array of TDetail;

var x: array of integer);

var

l0, l, i: integer;

currCut: TCutRecord;

maxCut: TCutRecord;

cutRecords: array[0..MAX_CUTRECORD_AMOUNT-1] of TCutRecord;

cutRecords1: array[1..MAX_CUTRECORD_AMOUNT] of TCutRecord;

i1, j1: integer;

begin

l0:=details[0].l;

for l:=l0 to materialLength do

begin

currCut.l:=l;

currCut.c:=0;

currCut.i:=0;

currCut.max_i:=-1;

maxCut.l:=0;

maxCut.c:=0;

maxCut.i:=0;

maxCut.max_i:=0;

j1:=0;

while true do

begin

if currCut.max_i=-1 then

begin

for i1:=0 to detailAmount-1 do

begin

if details[i1].l<=currCut.l then

begin

currCut.max_i:=i1;

currCut.i:=0;

end;

end;

end;

if (currCut.max_i=-1) or (currCut.i>currCut.max_i) then

begin

if j1<>0 then

begin

if currCut.c>maxCut.c then

begin

maxCut:=currCut;

end;

currCut:=cutRecords1[j1];

j1:=j1-1;

currCut.i:=currCut.i+1;

end

else

begin

break;

end;

end

else

begin

if (currCut.l>=l0) and (currCut.l<l) then

begin

if cutRecords[currCut.l].c+currCut.c>maxCut.c then

begin

maxCut:=cutRecords[currCut.l];

maxCut.c:=maxCut.c+currCut.c;

end;

currCut.i:=currCut.i+1;

continue;

end;

j1:=j1+1;

cutRecords1[j1]:=currCut;

currCut.l:=currCut.l-details[currCut.i].l;

currCut.c:=currCut.c+details[currCut.i].c;

currCut.max_i:=-1;

end;

end;

cutRecords[l]:=maxCut;

cutRecords[l].l:=l;

end;

for i:=0 to detailAmount-1 do

begin

x[i]:=0;

end;

l:=materialLength;

while l>=details[0].l do

begin

x[cutRecords[l].i]:=x[cutRecords[l].i]+1;

l:=l-details[cutRecords[l].i].l;

end;

end;

4. Описание программы

Вид главного окна программы приведено на рисунке:

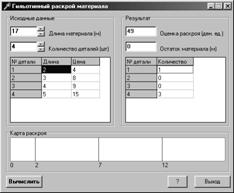
После запуска программы пользователю предлагается ввести длину материала и количество типов деталей, затем нужно заполнить поля таблицы с длиной и стоимостью каждой детали.

После ввода данных для решения нужно нажать кнопку "Вычислить", программа выдаст результат в виде таблицы с оптимальными значениями количества типов деталей. Также выводится общая оценка раскроя, остаток материала и наглядная карта раскроя проката в графической форме. Белые части раскроя обозначают типы деталей, красные линии – линии отреза материала. В случае остатка, соответствующая часть раскроя отображается серым цветом:

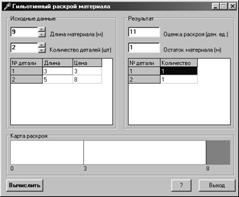
5. Контрольный пример

Пусть в задаче генерирования линейного раскроя заданы следующие параметры: длина проката L = 40, количество типов деталей m = 4, а значения длин l_i и стоимости c_i каждой детали приведены в таблице:

i	1	2	3	4
li	7	11	13	17
ci	9	14	16	22

Решаем задачу сеточным методом: сначала выполняем прямой ход. Выбираем начальное значение длины раскроя, равное минимальной длине детали: l₀ = min l_i = 7 и последовательно "шагаем" до конца проката, т.е. 40.

Чтобы найти максимальную стоимость на каждом шаге, мы перебираем все детали, которые могут поместиться в текущий раскрой, начиная с минимальной по длине. Для подсчета стоимости раскроя на текущем шаге мы вычитаем длину очередной выбранной детали из текущего раскроя и по таблице находим раскрой с длиной, равной полученному остатку и суммируем его оценку с оценкой выбранной детали. Из вычисленных оценок выбираем максимальную и заносим её в таблицу, вместе с номером детали, при которой эта оценка была получена.

Далее в таблице приведены результаты первого этапа (прямого хода) процесса:

l	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
f(l)	9	9	9	9	14	14	16	18	18	18	22	23	23	25	27	28	28
i(l)	1	1	1	1	2	2	3	1	1	1	4	1	1	1	1	2	2

l	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
f(l)	31	32	32	34	36	37	38	40	41	42	44	45	46	47	49	50	51
i(l)	1	1	1	1	1	1	3	1	1	2	4	1	1	1	1	1	1

Здесь и далее i(l) – номер детали, которой соответствует максимальная оценка раскроя (сумма стоимости всех деталей, входящих в раскрой) f(l) на шаге l.

Рассмотрим более подробно последовательное заполнение таблицы на примере шагов

l = 7…14, 22.

1) l = 7

Выбираем первую деталь: i = 1. Длина детали 7, оценка 9.

Вычисляем остаток от раскроя: 7 – 7 = 0. Поскольку остаток нулевой, то деталей, которые можно добавить в раскрой, нет. Следовательно, максимальная оценка текущего раскроя равна f = 9. Заносим в таблицу значения i(7) = 1, f(7) = 9 и переходим к следующему шагу раскроя.

2) l = 8

Снова берём первую деталь: i = 1. Длина детали 7, оценка 9.

Остаток: 8 – 7 = 1. Так как деталей с такой длиной нет, максимальная оценка раскроя f = 9. Заносим в таблицу i(8) = 1, f(8) = 9.

3) l = 9

i = 1, остаток 9 – 7 = 2, f = 9.

Заносим в таблицу i(9) = 1, f(9) = 9.

4) l = 10

i = 1, остаток 10 – 7 = 3, f = 9.

Заносим в таблицу i(10) = 1, f(10) = 9.

5) l = 11

i = 1, остаток 11 – 7 = 4, f = 9.

Учитывая, что в текущий раскрой также уместится деталь i = 2 c длиной 11, получим: i = 2, остаток 11 – 11 = 0, f = 14.

Сравним оценки раскроев. Выберем максимальную оценку (f = 14) и соответствующую ей деталь (i = 2).

Заносим в таблицу i(11) = 2, f(11) = 14.

6) l = 12

i = 1, остаток 12 – 7 = 5, f = 9.

i = 2, остаток 12 – 11 = 1, f = 14 (максимум)

Заносим в таблицу i(12) = 2, f(12) = 14.

7) l = 13

i = 1, остаток 13 – 7 = 6, f = 9.

i = 2, остаток 13 – 11 = 2, f = 14.

i = 3, остаток 13 – 13 = 0, f = 16 (максимум)

Заносим в таблицу i(13) = 3, f(13) = 16.

8) l = 14

i = 1, остаток 14 – 7 = 7.

Если мы видим, что длина остатка раскроя больше или равна начальному значению длины раскроя (l₀ = 7), т.е. в остаток может поместиться какая-либо деталь (в данном случае с индексом i = 1), из таблицы считываем значение оценки раскроя f(i) при i, равном значению остатка: f (7) = 9, тогда суммарная оценка раскроя f = f(7) + 9 = 9 + 9 = 18 (максимум)

i = 2, остаток 14 – 11 = 3, f = 14.

i = 3, остаток 14 – 13 = 1, f = 16.

Заносим в таблицу i(14) = 1, f(14) = 18.

…16) l = 22

i = 1, остаток 22 – 7 = 15, f (15) = 18, f = 18 + 9 = 27.

i = 2, остаток 22 – 11 = 11, f(11) = 14, f = 14 + 14 = 28 (максимум)

i = 3, остаток 22 – 13 = 9, f(9) = 9, f = 9 + 16 = 25.

i = 4, остаток 22 – 17 = 5, f = 22.

Заносим в таблицу i(22) = 2, f(22) = 28. и т.д., пока не достигнут конец проката.

Выполняем обратный ход (начинаем двигаться с конца таблицы):

1) l = 40

Из таблицы получаем индекс детали, добавленной в текущий раскрой: i(40) = 1.

Находим длину детали с полученным индексом: l₁ = 7.

Вычисляем остаток раскроя: 40 - 7 = 33. Этот остаток используем для следующего шага обратного хода.

2) l = 33

Индекс детали: i(33) = 2.

Длина детали: l₂ = 11.

Остаток раскроя: 33 - 11 = 22.

3) l = 22

Индекс детали: i(22) = 2.

Длина детали: l₂ = 11.

Остаток раскроя: 22 - 11 = 11.

4) l = 11

Индекс детали: i(11) = 2.

Длина детали: l₂ = 11.

Остаток раскроя: 11 - 11 = 0. Обратный ход закончен.

Теперь подсчитываем количество деталей каждого типа, которые мы получили при обратном ходе. Деталь с индексом i = 1 встретилась 1 раз, деталь с индексом i = 2 встретилась 3 раза.

Таким образом, искомый оптимальный раскрой характеризуется следующим четырёхмерным вектором x = (1; 3; 0; 0).

В вышеприведённой таблице с результатами прямого хода выделены номера заготовок, которые при обратном ходе последовательно включались в оптимальный раскрой.

Результат работы программы (проверка алгоритма):

Исходные данные

Длина проката: 40

Количество типов деталей: 4

Длина детали №1….: 7 Цена детали №1….: 9

Длина детали №2….: 11 Цена детали №2….: 14

Длина детали №3….: 13 Цена детали №3….: 16

Длина детали №4….: 17 Цена детали №4….: 22

Результат

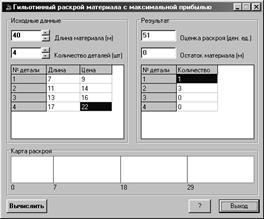
Оптимальное количество деталей каждого типа:

Деталь №1….: 1 шт.

Деталь №2….: 3 шт.

Деталь №3….: 0 шт.

Деталь №4….: 0 шт.

Оценка раскроя: 51 денежных единиц

Остаток материала: 0

Результаты ручного и машинного вычислений совпадают, что говорит о работоспособности разработанного алгоритма для ЭВМ.

Вывод

В данной работе поставленная задача была решена с помощью сеточного метода. Как показала проделанная работа, этот метод эффективен и прост для программной реализации на ЭВМ. Результат, полученный с помощью этого метода, является оптимальным. В нём реализуется целенаправленный перебор за конечное число шагов, в результате чего находится рациональный раскрой с максимумом прибыли.

В работе были произведены ручные вычисления и по ним проверена работа запрограммированного алгоритма на ЭВМ. Разработанная программа и сеточный метод оптимизации раскроя достаточно универсальны. Они могут применяться в различных отраслях промышленности при массовом производстве, при этом в алгоритм следует вносить коррективы, связанные с учетом технологии производства и применяемого оборудования.

Текст программы

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,

StdCtrls, Grids, ComCtrls, ExtCtrls;

type

//деталь

TDetail=record

l: integer;//длина

c: integer;//цена

end;

//запись раскроя

TCutRecord=record

l: integer;//длина

c: integer;//цена

i: integer;//индекс детали

max_i: integer;//максимальный индекс детали для текущей длины материала

end;

TForm_Main = class(TForm)

GroupBox1: TGroupBox;

Edit_MaterialLength: TEdit;

Label_MaterialLength: TLabel;

UpDown_MaterialLength: TUpDown;

Label_DetailAmount: TLabel;

UpDown_DetailAmount: TUpDown;

Edit_DetailAmount: TEdit;

StringGrid_In: TStringGrid;

GroupBox2: TGroupBox;

StringGrid_Out1: TStringGrid;

Button_Calculate: TButton;

Button_Exit: TButton;

GroupBox3: TGroupBox;

Image_Cut: TImage;

Edit1: TEdit;

Edit2: TEdit;

Label1: TLabel;

Label2: TLabel;

Button1: TButton;

procedure Button_ExitClick(Sender: TObject);

procedure Edit_DetailAmountChange(Sender: TObject);

procedure FormCreate(Sender: TObject);

procedure Edit_MaterialLengthChange(Sender: TObject);

procedure Button_CalculateClick(Sender: TObject);

procedure Button1Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

const

MAX_DETAIL_AMOUNT=10;//максимальное кол-во деталей

MAX_CUTRECORD_AMOUNT=10000;//максимальное кол-во записей раскроя

MAX_MATERIAL_LENGTH=10000;//максимальная длина материала

var

Form_Main: TForm_Main;

materialLength: integer;//длина материала

detailAmount: integer;//кол-во деталей

details: array[1..MAX_DETAIL_AMOUNT] of TDetail;//детали

x: array[1..MAX_DETAIL_AMOUNT] of integer;//результат

implementation

uses Unit2;

{$R *.DFM}

//процедура вычисления рационального раскроя

procedure searchRationalCut(

materialLength: integer;

detailAmount: integer;

var details: array of TDetail;

var x: array of integer);

var

l0, l, i: integer;

currCut: TCutRecord;

maxCut: TCutRecord;

cutRecords: array[0..MAX_CUTRECORD_AMOUNT-1] of TCutRecord;

cutRecords1: array[1..MAX_CUTRECORD_AMOUNT] of TCutRecord;

i1, j1: integer;

begin

l0:=details[0].l;

for l:=l0 to materialLength do

begin

currCut.l:=l;

currCut.c:=0;

currCut.i:=0;

currCut.max_i:=-1;

maxCut.l:=0;

maxCut.c:=0;

maxCut.i:=0;

maxCut.max_i:=0;

j1:=0;

while true do

begin

if currCut.max_i=-1 then

begin

for i1:=0 to detailAmount-1 do

begin

if details[i1].l<=currCut.l then

begin

currCut.max_i:=i1;

currCut.i:=0;

end;

end;

end;

if (currCut.max_i=-1) or (currCut.i>currCut.max_i) then

begin

if j1<>0 then

begin

if currCut.c>maxCut.c then

begin

maxCut:=currCut;

end;

currCut:=cutRecords1[j1];

j1:=j1-1;

currCut.i:=currCut.i+1;

end

else

begin

break;

end;

end

else

begin

if (currCut.l>=l0) and (currCut.l<l) then

begin

if cutRecords[currCut.l].c+currCut.c>maxCut.c then

begin

maxCut:=cutRecords[currCut.l];

maxCut.c:=maxCut.c+currCut.c;

end;

currCut.i:=currCut.i+1;

continue;

end;

j1:=j1+1;

cutRecords1[j1]:=currCut;

currCut.l:=currCut.l-details[currCut.i].l;

currCut.c:=currCut.c+details[currCut.i].c;

currCut.max_i:=-1;

end;

end;

cutRecords[l]:=maxCut;

cutRecords[l].l:=l;

end;

for i:=0 to detailAmount-1 do

begin

x[i]:=0;

end;

l:=materialLength;

while l>=details[0].l do

begin

x[cutRecords[l].i]:=x[cutRecords[l].i]+1;

l:=l-details[cutRecords[l].i].l;

end;

end;

//ввод данных пользователя из таблицы

procedure updateData;

var

i: integer;

begin

materialLength:=strToInt(Form_Main.Edit_MaterialLength.Text);

detailAmount:=strToInt(Form_Main.Edit_DetailAmount.Text);

for i:=1 to detailAmount do

begin

details[i].l:=strToInt(Form_Main.StringGrid_In.Cells[1,i]);

details[i].c:=strToInt(Form_Main.StringGrid_In.Cells[2,i]);

end;

end;

//графическое отображение рационального раскроя

procedure drawRationalCut(

image: TImage;

materialLength: integer;

detailAmount: integer;

details: array of TDetail;

x: array of integer);

var

i, j: integer;

sum: integer;

k_x: real;

curr_x: integer;

curr_x_scr: real;

begin

sum:=0;

for i:=0 to detailAmount-1 do

begin

sum:=sum+x[i]*details[i].l;

end;

k_x:=image.width/materialLength;

with image.Canvas do

begin

brush.Style:=bsSolid;

brush.Color:=clBtnFace;

fillRect(rect(0, 0, image.width, image.height));

brush.Color:=clGray;

pen.Color:=clGray;

rectangle(trunc(k_x*sum), 0, trunc(k_x*materialLength), 50);

brush.Color:=clWhite;

pen.Color:=clGray;

rectangle(0, 0, trunc(k_x*sum), 50);

pen.Color:=clRed;

brush.Style:=bsClear;

textOut(0,51,'0');

curr_x:=0;

curr_x_scr:=0;

for i:=0 to detailAmount-1 do

begin

for j:=0 to x[i]-1 do

begin

curr_x:=curr_x+details[i].l;

curr_x_scr:=curr_x_scr+k_x*details[i].l;

if curr_x<>materialLength then

begin

moveTo(trunc(curr_x_scr),0);

lineTo(trunc(curr_x_scr),50);

textOut(trunc(curr_x_scr), 51, intToStr(curr_x));

// textOut(trunc(curr_x_scr-15), 21, '('+intToStr(i+1)+')');

end;

end;

end;

end;

end;

//выход из программы

procedure TForm_Main.Button_ExitClick(Sender: TObject);

begin

close;

end;

//изменение кол-ва детеалей

procedure TForm_Main.Edit_DetailAmountChange(Sender: TObject);

var

new_d_a: integer;

i: integer;

begin

new_d_a:=strToInt(Form_Main.Edit_DetailAmount.Text);

if (new_d_a>=1) then

begin

if (new_d_a<=MAX_DETAIL_AMOUNT) then

begin

Form_Main.StringGrid_In.RowCount:=new_d_a+1;

for i:=1 to new_d_a do

begin

Form_Main.StringGrid_In.Cells[0,i]:=intToStr(i);

end;

end

else

begin

Form_Main.Edit_DetailAmount.Text:=intToStr(MAX_DETAIL_AMOUNT);

end;

end

else

begin

Form_Main.Edit_DetailAmount.Text:=intToStr(1);

end;

end;

//инициализация программы

procedure TForm_Main.FormCreate(Sender: TObject);

begin

Form_Main.UpDown_MaterialLength.Min:=1;

Form_Main.UpDown_MaterialLength.Max:=MAX_MATERIAL_LENGTH;

Form_Main.UpDown_DetailAmount.Min:=1;

Form_Main.UpDown_DetailAmount.Max:=MAX_DETAIL_AMOUNT;

Form_Main.StringGrid_In.Cells[0,0]:='№ детали';

Form_Main.StringGrid_In.Cells[1,0]:='Длина';

Form_Main.StringGrid_In.Cells[2,0]:='Цена';

Form_Main.StringGrid_In.Cells[0,1]:='1';

Form_Main.StringGrid_Out1.Cells[0,0]:='№ детали';

Form_Main.StringGrid_Out1.Cells[1,0]:='Количество';

end;

//изменение длины материала

procedure TForm_Main.Edit_MaterialLengthChange(Sender: TObject);

var

new_m_l: integer;

begin

new_m_l:=strToInt(Form_Main.Edit_MaterialLength.Text);

if (new_m_l>=1) then

begin

if not (new_m_l<=MAX_MATERIAL_LENGTH) then

begin

Form_Main.Edit_MaterialLength.Text:=intToStr(MAX_MATERIAL_LENGTH);

end;

end

else

begin

Form_Main.Edit_MaterialLength.Text:=intToStr(1);

end;

end;

//сортировка данных по возрастанию длины детали

procedure StrGridSort;

var

i: integer;

do_next: boolean;

begin

do_next:=true;

while do_next do

begin

do_next:=false;

for i:=1 to Form_Main.StringGrid_In.RowCount-2 do

begin

if strToInt(Form_Main.StringGrid_In.Cells[1,i])>

strToInt(Form_Main.StringGrid_In.Cells[1,i+1]) then

begin

Form_Main.StringGrid_In.cols[1].Exchange(i,i+1);

Form_Main.StringGrid_In.cols[2].Exchange(i,i+1);

do_next:=true;

end;

end;

end;

end;

//вычисление рационального раскроя и отображение результата

procedure TForm_Main.Button_CalculateClick(Sender: TObject);

var

i,sum,cost: integer;

begin

strGridSort;

updateData;

searchRationalCut(materialLength, detailAmount, details, x);

Form_Main.StringGrid_Out1.RowCount:=detailAmount+1;

sum:=0; cost:=0;

for i:=1 to detailAmount do

begin

Form_Main.StringGrid_Out1.Cells[0,i]:=intToStr(i);

Form_Main.StringGrid_Out1.Cells[1,i]:=intToStr(x[i]);

sum:=sum+x[i]*details[i].l;

cost:=cost+x[i]*details[i].c;

end;

Form_Main.Edit1.Text:=intToStr(cost);

Form_Main.Edit2.Text:=intToStr(materialLength-sum);

drawRationalCut(Form_Main.Image_Cut, materialLength, detailAmount, details, x);

end;

procedure TForm_Main.Button1Click(Sender: TObject);

begin

Form2.Show;

end;

end.

Литература

1. Э.А. Мухачева "Рациональный раскрой промышленных материалов". Москва, Машиностроение, 1984 г.

2. Э.А. Мухачева, Г.Ш. Рубинштейн "Математическое программирование". Новосибирск, Наука, 1977 г.