Навигация
Динамический анализ с использованием дерева контекстов
3.2 Динамический анализ с использованием дерева контекстов
Эта схема анализа описана в работе [4] и в несколько измененном виде приводится здесь.
Введем следующую терминологию.
Дерево контекстов (context tree) CV(p) программы p — дерево, состоящее из вершин следующих типов: функция, цикл, оператор вызова функции или доступа к памяти, условный оператор, и другие типы операторов, присутствующие в языке. Между двумя вершинами есть ребро, если одна из них непосредственно вызывает другую. Корень дерева – функция main(), основное тело программы или другое аналогичное понятие из используемого языка программирования.
Контекст — это путь от корня до любой вершины дерева контекстов.
Пусть вершина S(a) соответствует оператору доступа к памяти a. Контекст CV(a) оператора a — путь от корня дерева контекстов к вершине S(a).
Контекст функции (цикла) — путь от корня дерева контекстов к вершине, соответствующей этой функции (циклу).
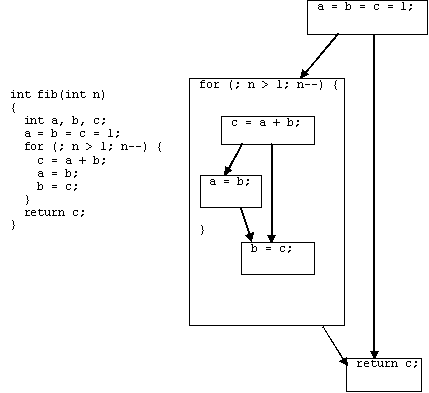
Рассмотрим пример.
int A[10], B[10];
void main() {
for (int i=0; i<10; i++)/* f1 */
proc(i);/* st1 */
}
void proc(int i) {
for (int m=0; m<10; m++) {/* f2 */
if (i%2 == 0)/* if1 */
A[m] = ...;/* st2 */
else
... = A[m];/* st3 */
B[m] = ...;/* st4 */
}
}
В этом примере оператор st2 может иметь контекст C(a) = (main f1 st1 proc f2 if1 st2). В случае наличия рекурсивной функции rfunc контекст мог бы быть таким: C(a) = (… rfunc st1 rfunc st1 rfunc …).
Цепочка векторов итераций (iteration vector chain) IVC(a) — это список номеров итераций для каждого узла-цикла контекста C(a). Если контекст не содержит циклов, то список не будет содержать ни одного элемента.
Цепочка векторов итераций относится к конкретному моменту выполнения программы, поэтому каждый оператор может иметь несколько разных IVC. Так, например, для оператора st2 может быть IVC(a) = (1, 4) или IVC(a) = (4, 1).
Виртуальная точка доступа a (virtual point) — это пара VP(a) = (C(a), IVC(a)).
Для каждой ячейки памяти анализатор хранит виртуальные точки последней записи и всех чтений с момента последней записи. Это позволяет обнаружить все зависимости по данным, возникающие в программе.
Алгоритм нахождения прямых зависимостей.
Для каждой операции чтения ar:
Определить ячейку памяти, читаемую ar.
Определить виртуальную точку VP(aw) последней записи aw в эту ячейку.
Найти контекст CL – длиннейший общий подпуть контекстов C(ar) и C(aw).
Найти контекст Cm – длиннейший контекст, являющийся подконтекстом контекста CL таким, что соответствующие цепочки IVC(ar) и IVC(aw) содержат одинаковые значения на отрезке, соответствующем контексту Cm.
Пусть r и w – векторы, образованные отрезками цепочек IVC(ar) и IVC(aw), не вошедшими в контекст Cm. Вычислить расстояние d = r – w, если dim(r)>0 и положить d=[] иначе.
Пусть f1 – самый «глубокий» цикл в контексте СL. Добавить зависимость между итерациями цикла f1 (и обрамляющих циклов) с расстоянием d.
Вместо п.6 можно записать зависимость между конкретными операторами в теле цикла. Пусть st1 и st2 – вершины C(ar) и C(aw), непосредственно следующие за CL. Добавить зависимость st1 от st2 с расстоянием d. Поскольку в данной работе рассматривается только распараллеливание циклов, в текущем анализаторе этого не делается.
Похожие алгоритмы нужно применять для нахождения обратных и зависимостей по выходу. При нахождении зависимостей по выходу надо для каждой операции записи искать предшествующую операцию записи. Для нахождения обратных зависимостей необходимо для всех операций записи обрабатывать все предшествующие им чтения ячейки памяти с момента последней записи в ту же ячейку.
3.3 Динамический анализ с использованием глобальных номеров итераций
Другой подход к динамическому анализу использует понятие глобальных номеров итераций (GIN – Global Iteration Number) [5]. Это означает, что все итерации всех циклов нумеруются по порядку. Например, в следующем примере
for (i=1; i<=3; i++)
for (j=1; j<=3; j++)
A[f1(i,j)]= ... A[f2(i,j)] ...;
глобальные номера итераций будут распределены следующим образом:
| (1,–) 1 | (1,1) 2 | (1,2) 3 | (1,3) 4 |
| (2,–) 5 | (2,1) 6 | (2,2) 7 | (2,3) 8 |
| (3,–) 9 | (3,1) 10 | (3,2) 11 | (3,3) 12 |
Здесь в каждой клетке в первой строчке показаны значения индексов циклов (i,j), а во второй – соответствующий глобальный номер итерации. Запись (i,–) означает, что в момент начала итерации внешнего цикла внутренний цикл еще не активен.
Данный метод используется для нахождения зависимостей между итерациями циклов. При входе в цикл запоминается GIN первой итерации. Кроме того, при входе в очередную итерацию цикла запоминается GIN текущей итерации, а GIN предыдущей итерации добавляется в специальный буфер, в котором записаны k последних итераций этого цикла (k – это емкость буфера). При вычислении расстояний для зависимостей этот буфер будет просматриваться в поисках подходящей итерации, поэтому метод позволяет определить расстояние, если оно не превосходит k, либо установить, что оно превышает k. Для каждой ячейки памяти запоминается GIN последней записи для отслеживания прямых зависимостей и зависимостей по выходу, а также предшествующих чтений, для того чтобы отслеживать также и обратные зависимости.
Рассмотрим случай, когда некоторая ячейка массива A записывается на итерации (2, 2), а затем читается на итерации (2, 3). К моменту чтения состояние выполнения программы будет таким:
| Цикл | Начало цикла | Текущая итерация | Буфер |
| i | 1 | 5 | 1 |
| j | 6 | 8 | 7,6 |
Запись в ячейку массива имела GIN = 7. Это было на той же итерации внешнего цикла. Просмотрев буфер цикла по j, можно вычислить расстояние между записью и чтением, равное 1.
Теперь пусть запись производилась на итерации (1,1), а чтение на итерации (3,3). Состояние программы в момент чтения:
| Цикл | Начало цикла | Текущая итерация | Буфер |
| i | 1 | 9 | 5,1 |
| j | 10 | 12 | 11,10 |
Запись в массив (GIN = 2) произошла не в текущем цикле (2 < 10), а в объемлющем цикле (1 <= 2 <= 9). Просматривая буфер цикла по i в поисках итерации с GIN <= 2, мы определяем расстояние, равное 2.
В сущности, данный метод позволяет делать то же самое, что и предыдущий, но только на уровне целых итераций циклов, а не отдельных операторов и использует при этом другие технические решения. Помимо этого, предыдущий метод вводит удобное понятие дерева контекстов, которое может быть использовано также и для иных целей кроме динамического анализа. Поэтому в рамках данной работы реализовывался метод дерева контекстов.
Похожие работы
... для хранения директив FortranDVM, формирование которых осуществляет блок распределения вычислений и данных, и методы для их вставки, а также реализован экспорт этих комментариев в файл. 3.3 Алгоритмы Реализованные в дипломной работе классы блока статического построения расширенного графа управления программы и вспомогательных структур данных содержат большое число членов-методов, решающих ...
... из-за динамической подзагрузки программы из файловой системы) и отлаживать его производительность по той же методике, которая была описана выше применительно к программе целиком. 5. Средство анализа эффективности MPI программ 5.1 Постановка задачи В системе DVM существуют развитые средства анализа эффективности выполнения параллельной DVM-программы. Эти средства являются более мощными, ...
... лишь контекстным анализом. Как было отмечено в [12], применение глубокого статического анализа программ может позволить существенно снизить количество ложных срабатываний и повысить точность обнаружения уязвимостей защиты. 4.3. Использование методов анализа потоков данных для решения задачи обнаружения уязвимостей В отделе компиляторных технологий по контракту с фирмой Nortel Networks ...
... практичных алгоритмов оптимизированного перебора, позволяющих за разумное время осуществлять распараллеливание достаточно больших участков. Анализ работ, посвященных оптимизации кода для процессоров с параллелизмом на уровне команд показывает, что для достижения наилучших результатов необходимо применение комплекса оптимизаций, среди которых можно выделить следующие классы. Преобразования циклов ...
0 комментариев