Навигация
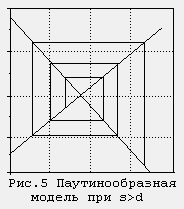
Паутинообразная модель фирмы
14872
знака
10
таблиц
2
изображения
Тема: "ПАУТИНООБРАЗНАЯ" МОДЕЛЬ ФИРМЫ
1. ВВЕДЕНИЕ
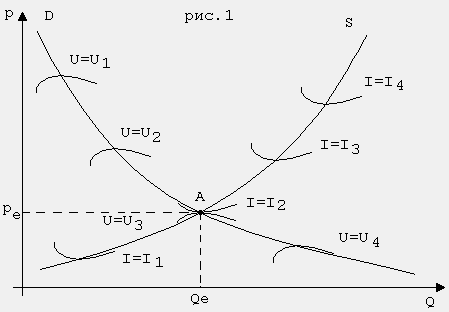
Пусть предприниматель собирается вложить средства в создание фирмы, которая будет выпускать товар и реализовывать его на рынке. Его интересует, как будет вести себя цена на товар при изменении объема производства. Опыт подсказывает, что при увеличении производства происходит падение спроса и приходится снижать цену. Ему хотелось бы знать, при каких условиях пена будет стабильной. Можно ли дать ответ на этот вопрос с помощью математической модели?
Консультант объясняет, что в литературе описано несколько вариантов такой модели. Все они обладают определенными одинаковыми свойствами. Обычно в них предполагается, что спрос на некоторый продукт (чаще всего рассматривается сельскохозяйственная продукция) на заданном отрезке времени зависит от цены (и других факторов) на этом отрезке. Что же касается предложения, то оно определяется ценами предыдущего периода времени (недели, месяца, квартала и т. д). Кроме того, предполагается, что рынок всегда находится в условиях локального равновесия. Исторически такая модель получила название "Паутинообразной", вероятно, потому, что такого же принципа "учета предыдущего шага" придерживается паук, когда он ткет паутину.
Существуют четыре варианта этой модели: детерминированная, вероятностная, модель с обучением и модель с запасами,
Предприниматель интересуется, чем они отличаются друг от друга?
Консультант отвечает, что в детерминированной модели отсутствует учет случайных факторов. В вероятностной модели учитываются влияние на спрос непредвиденных колебаний предпочтений и доходов потребителей, а также другие случайные факторы, влияющие на величину спроса. Предложение на предыдущем отрезке времени также считается подверженным наличию случайных факторов. Они отражают влияние колебаний технологии и эффективности производственного процесса и т д. Наконец, условие локального равновесия означает совпадение спроса и предложения с точностью до некоторой случайной величины.
В модели с обучением предполагается, что поставщики учитывают сложившуюся тенденцию изменения цен и с учетом этого планируют выпуск продукции на очередной отрезок времени.
В вероятностной модели и в модели с обучением цены устанавливаются на таком уровне, чтобы обеспечить локальное равновесие рынка только за счет текущего производства, и никаких запасов продукции не создается (например, потому, что продуты быстро портятся).
В модель с запасами вводится дополнительная группа участников рыночного механизма, которых можно назвать "коммерсантами". Они держат запасы и организуют торговлю.
Предприниматель считает, что для его случая, наверное, больше подойдет вероятностная модель с обучением. Его интересует, при каких допущениях она составлена? Как выглядит зависимость для определения текущего спроса?
Консультант отвечает: "Предполагается, что спрос на Т-м отрезке времени линейно зависит от текущей цены и, кроме того, спрос подвержен случайному разбросу. Таким образом, для описания спроса нужно задать коэффициенты линейного уравнения: (например А и В) и случайную величину (например. UТ), имеющую заданное распределение."
В результате получается расчетная формула следующего вида:
| D T= A – B*PT + UT, | (1) |
где: D T– спрос на Т-м отрезке;
А, В - коэффициенты линейного уравнения;
РТ - подлежащая определению цена на Т-м отрезке времени;
UT - случайная величина с заданным законом распределения.
Предприниматель интересуется, что означает знак "минус"?
Консультант отвечает, что с повышением цены спрос на продукцию снижается.
Предпринимателя интересует, какое именно распределение следует выбрать в этом случае?
Логично предположить, что спрос симметрично колеблется относительно среднего значения, которое определяется постоянными коэффициентами линейного уравнения. Поэтому можно выбрать нормальное распределение с нулевым математическим ожиданием и заданным средним квадратическим отклонением (СКО) – σu.
Как определяется предложение?
Предполагается, что предложение на текущем отрезке также линейно зависит от цены, но не текущей, а представляющей собой некоторую комбинацию цен на двух предыдущих отрезках времени. В простейшем случае это может быть средняя цена. Поэтому, для расчета предложения используется следующая зависимость:
| SТ=С+Е*Р( | (2) |
где SТ – предложение на Т-м отрезке времени;
С, Е – коэффициенты линейного уравнения;
Р(
) – среднее (точнее, средневзвешенное) значение цены на двух предыдущих отрезках времени;
VТ - случайная величина с заданным законом распределения.
Предприниматель интересуется: "И опять нормальное распределение?"
Да, конечно, с теми же основаниями. Только с другим СКО –σv.
А как определяется средняя цена за предшествующий период?
Средневзвешенная цена определяется по формуле:
| Р( | (3) |
Нетрудно убедиться в том, чтo при = 0 средневзвешенная цена Р(р) = РТ-1 . Это означает, что обучение в модель не заложено. Для другого крайнего случая (при = 1) средневзвешенная цена Р() = РТ-2. Это также означает, что обучение в модели отсутствует, но для определения предложения используется более удаленная цена, Наконец, при = 0,5 средневзвешенная цена Р() равна среднему арифметическому значению из цен РТ-1 и РТ-2.
Еще добавить уравнение локального равновесия рынка, которое можно записать так:
| st = dt+wt, | (4) |
где SТ — предложение на Т-м отрезке времени;
DT — спрос на Т-м отрезке времени;
WТ — случайная величина с заданным распределением.
Примем опять нормальное распределение. Для выбора других распределений нет особых оснований. Можно было бы взять усеченное нормальное распределение, но не ясно, какова должна быть величина усечений. Случайная величина WТ характеризуется нулевым математическим ожиданием н средним квадратическим отклонением σw.
А как же все-таки в модели определяется закон изменения цены на продукт во времени?
Система уравнений (1), (2), (З) н (4) после преобразований сводится к выражению вида:
| РТ = F(PT-1, PT-2) | (5) |
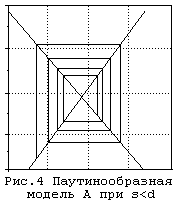
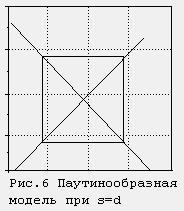
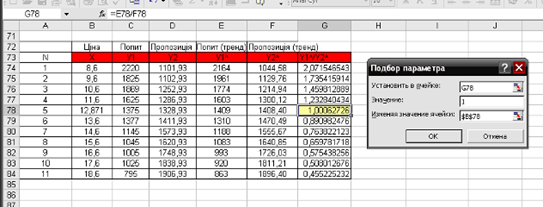
Вначале необходимо каким-либо приближенным способом определить цену для первых двух отрезков времени. После этого можно производить вычисления по зависимости (5) неограниченное число раз. Результаты расчетов удобнее всего представить в виде графика.
Похожие работы
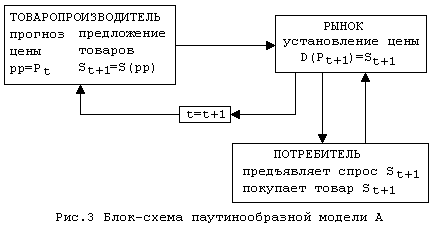
... моделей. Дискретные модели вида (4) представляют интерес потому, что в них более последовательно, чем в непрерывных, отражаются процедуры принятия решений. Паутинообразная модель с запаздыванием спроса Концептуальная модель любого процесса динамики цен включает взаимодействие трех подсистем, которые можно условно назвать “товаропроизводитель”, “потребитель” и “рынок” (рис.2). Паутинообразная ...
... модель при переменных параметрах роста населения, изменениях технического прогресса, а значит капиталовооруженности труда и изменениях нормы сбережений. Из неоклассической модели Солоу следует, что в условиях совершенной конкуренции при любой норме сбережений рыночная экономика тяготеет к сбалансированному росту, при котором национальный доход и капитал увеличиваются с темпом, равным темпу роста ...
... значение критерия . Табличное значение критерия при надежности Р=0,95 и степенях свободы k1 = 1, k2 = n – 2 = 9 равняется 5,12, поскольку наблюдаемое значение больше критического, то эта линейная модель является адекватной. Используя t-статистику, с надежностью Р=0,95 оценим значимость коэффициента корреляции. Вычислим наблюдаемое значение t-статистики . Табличное значение -критерия ...
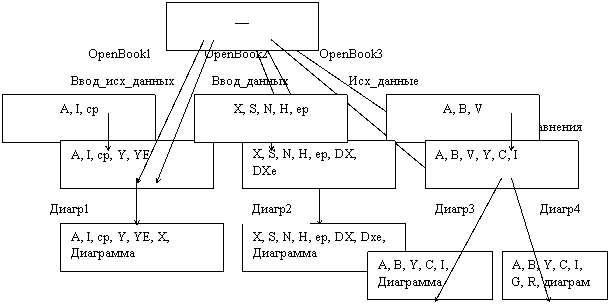
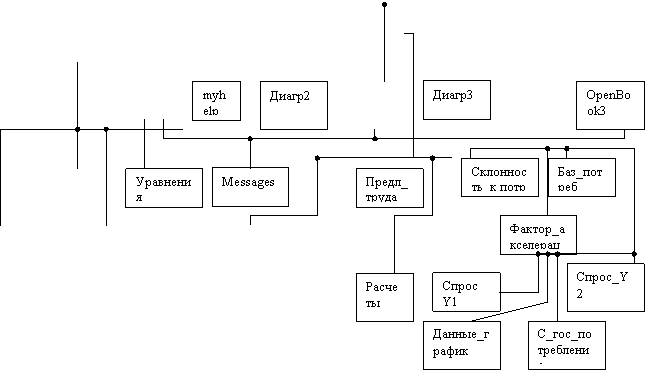
... графиков невозможно. В связи с этим для пользователя удобнее, если пакет реализуется как пакет, работающий в режиме диалогового сопровождения. 2.3 Построение модели предметной области При решении задачи определения макроэкономических показателей в пакете используется определенная совокупность данных и связей между ними, или модель предметной области (МПО). В этой совокупности можно выделить ...
0 комментариев