Перетворення координат, операції масштабування в бібліотеці Opengl

МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ

Бердичівський політехнічний коледж

КОНТРОЛЬНА РОБОТА

з предмета “Комп’ютерна графіка”

(варіант №8)

Перетворення координат, операції масштабування

в бібліотеці Opengl

м. Бердичів 2007 р.

1. Перетворення координат: афінне перетворення на площині, тривідерне афінне перетворення

Спочатку розглянемо загальні питання перетворення координат. Нехай задана n-вимірна система координат у базисі (k1 ,k2, ..., kn), яка описує положення точки у просторі за допомог гою числових значень kі. У КГ найчастіше використовуються двовимірна (п = 2) та тривимірна (п = 3) системи координат.

Якщо задати іншу, N-вимірну, систему координат у базисі (т1, т2, ..., mN), і поставити задачу визначення координат у новій системі, знаючи координати в старій, то рішення (якщо воно існує) можна записати у такому вигляді:

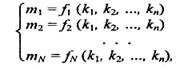
де fi— функція перерахування i-ї координати, аргументами є координати у системі ki. Можна поставити й обернену задачу: по відомих координатах (m1 ,т2, .... mN), визначити координати (к1 ,к2, ..., кn). Рішення оберненої задачі запишемо так:

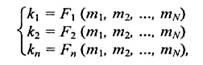
де Fi — функції оберненого перетворення.

У випадку, коли розмірності систем координат не збігаються (п N), здійснити однозначне перетворення координат найчастіше не вдається. Наприклад, за двовимірними екранними координатами не можна без додаткових умов однозначно визначити тривимірні координати об'єктів, що відображаються.

Якщо розмірності систем збігаються (n = N), то також можливі випадки, коли не можна однозначно вирішити пряму або обернену задачі. Перетворення координат класифікують:

• за системами координат — наприклад, перетворення з полярної системи у прямокутну;

• за видом функції перетворення .

За видом функцій перетворення розрізняють лінійні та нелінійні перетворення. Якщо

при усіх i= і, 2, ..., N функції fi — лінійні відносно аргументів (k1 ,k2, ..., kn), тобто

де aij — константи, то такі перетворення називаються лінійними, а при n = N— афінними. Якщо хоча б для одного i функція fi є нелінійною відносно (k1 ,k2, ..., kn), тоді перетворення координат у цілому є нелінійним. Наприклад, перетворення

нелінійне, оскільки є добуток ху у виразі для Y. Тим, хто цікавиться математичними аспектами, що відносяться до систем координат і перетворення систем координат, можна порекомендувати такі книги, як [15, 23].

Лінійні перетворення наглядно записуються в матричній формі:

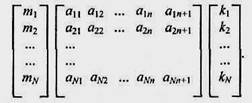
Тут матриця коефіцієнтів (аіj) множиться на матрицю-стовпець (ki), й у результаті матимемо матрицю-стовпець (mi).

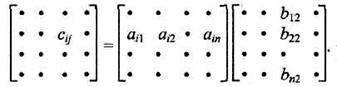
Ми й далі часто будемо використовувати множення матриць, тому зробимо невеличкий екскурс у матричну алгебру. Для двох матриць — матриці А розмірами (т*п) та В — (п*р):

матричним добутком є матриця С = АВ розмірами (т*р)

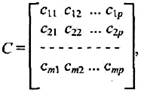
для якої елементи cij обраховуються за формулою  .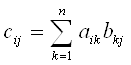

Правило обчислення елементів матриці С можна легко запам'ятати за назвою "рядок на стовпець". І дійсно, для обчислення будь-якого елемента cij необхідно помножити елементи і-го рядка матриці А на елементи j -го стовпця матриці В.

Добуток матриць визначається тільки для випадку, коли кількість стовпців матриці А дорівнює кількості рядків матриці В. Більш докладно з матрицями ви можете ознайомитися в математичній літературі, наприклад, у [5]. Тепер повернемося знову до перетворень координат. Розглянемо більш докладно деякі окремі типи перетворень.

Афінне перетворення на площині

Задамо якусь двовимірну систему координат (х, у). Афінне перетворення на площині описується формулами

де А, В, ..., F — константи. Значення (X, Y) можна розглядати як координати в новій системі координат.

Обернене перетворення (X, Y) у (х, у) також є афінним:

Афінне перетворення зручно записувати в матричному вигляді. Константи А, В, .... F утворюють матрицю перетворення, котра, будучи помножена на матрицю-стовпець координат (х, у) дає матрицю-стовпець (X, У). Однак щоб урахувати константи С та F, необхідно перейти до так званих однорідних координат — додамо ще один рядок у матрицях координат:

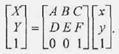
Матричний запис дає можливість наочно описувати декілька перетворень, що йдуть одні за одними. Наприклад, якщо необхідно спочатку виконати перетворення

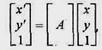
а потім — інше перетворення

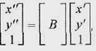
то це можна описати як

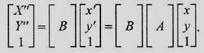
Однак замість двох перетворень можна виконати тільки одне

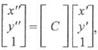
де матриця С дорівнює добутку ВА.

Тепер розглянемо окремі випадки афінного перетворення.

1.   Паралельний зсув координат (рис. 2.1).

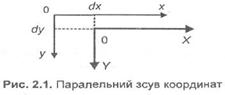
У матричній формі:

Обернене перетворення: