Навигация
Симметричность относительно центра эксперимента. Это значит, что алгебраическая сумма элементов вектор – столбца для каждого фактора равна 0, т.е
1. Симметричность относительно центра эксперимента. Это значит, что алгебраическая сумма элементов вектор – столбца для каждого фактора равна 0, т.е.
![]() ij=0 (4 )
ij=0 (4 )
где i – номер фактора (i=1,n);
j – номер опыта (j=1,N ).
2. Условием нормировки, т.е. сумма квадратов элементов каждого столбца равна числу опытов:
![]() ij2= N (i=1,n) (5 )
ij2= N (i=1,n) (5 )
3.Ортогональностью, это означает, что сумма почленных произведений любых двух вектор- столбцов матрицы равна 0, т.е.
![]() ij *хkj=0 (i
ij *хkj=0 (i![]() k; i, k=1,n) (6 )
k; i, k=1,n) (6 )
Данные свойства, особенно условие ортогональности, позволяют значительно упростить определение коэффициентов уравнения множественной регрессии. В этом случае оценки коэффициентов регрессионной модели можно вычислить по формуле:
ai=![]() ij*yj /N (i=0,n) (7 )
ij*yj /N (i=0,n) (7 )
А коэффициенты парных взаимодействий соответственно по формуле:
aik=![]() ij*xkj*yj /N (i
ij*xkj*yj /N (i![]() k; i, k=1,n) (8)
k; i, k=1,n) (8)
Количество испытаний в ПФЭ значительно превосходит число определяемых коэффициентов линейной модели плана эксперимента, т.е. ПФЭ обладает большой избыточностью и поэтому возникает проблема сокращения числа опытов. В связи с этим используется дробный факторный эксперимент (ДФЭ), который представляет часть полного факторного эксперимента. Матрица планирования для дробного факторного эксперимента называется дробной репликой. Различают регулярные и нерегулярные дробные реплики.
Регулярные реплики образуются из ПФЭ 2n делением пополам, на четыре части, восемь частей ит.д., т.е. на число кратное 2. Они называются соответственно: полурепликой, четверть- репликой, ![]() - реплики и т.д.. ДФЭ обозначается как 2n-k, где
- реплики и т.д.. ДФЭ обозначается как 2n-k, где
k – кратность деления ПФЭ 2n на части 2k. Например, ДФЭ типа 4-2 означает, что ПФЭ из N=24=16 делится на 22=4 и получается план эксперимента, состоящий из N=24-2=4 опытов.
Если регулярные реплики умножить на нечетные числа, больше единицы, то получаются нерегулярные реплики. Как например, ![]() реплики,
реплики, ![]() реплики,
реплики, ![]() реплики и т.д. являются нерегулярными.
реплики и т.д. являются нерегулярными.
Использование ДФЭ позволяет значительно сократить количество экспериментов и тем самым сэкономить ресурсы ЭВМ.
2.2 Пример планирования машинного эксперимента для модели СМО
Пусть необходимо провести машинный эксперимент по определению функциональной зависимости среднего времени ожидания заявки в очереди (![]() ож) от факторов: интенсивность поступления заявок λ, интенсивности обслуживания μ и емкости буфера L для однофазной одноканальной системы массового обслуживания со следующими параметрами: интенсивность поступления заявок λ=15
ож) от факторов: интенсивность поступления заявок λ, интенсивности обслуживания μ и емкости буфера L для однофазной одноканальной системы массового обслуживания со следующими параметрами: интенсивность поступления заявок λ=15![]() 5
5![]() ; интенсивность обслуживания μ=10
; интенсивность обслуживания μ=10![]() 5
5![]() ; количество мест в очереди L=10
; количество мест в очереди L=10![]() 2.
2.
Для определения заданной зависимости представим математическую модель системы в виде:
y= a0+a1x1+a2x2+a3x3, (9)
x1= λ ; x2= μ ; x3= L ; y=![]() ож
ож
Так как порядок модели n=3, то матрица планирования для полного факторного эксперимента примет вид (Таблица 2).
Таблица 2. Матрица планирования для модели СМО
| Номер опыта | х0 | х1 | х2 | х3 | y |
| 1 | +1 | -1 | -1 | -1 |
|
| 2 | +1 | +1 | -1 | -1 |
|
| 3 | +1 | -1 | +1 | -1 |
|
| 4 | +1 | +1 | +1 | -1 |
|
| 5 | +1 | -1 | -1 | +1 |
|
| 6 | +1 | +1 | -1 | +1 |
|
| 7 | +1 | -1 | +1 | +1 |
|
| 8 | +1 | +1 | +1 | +1 |
|
При этом следует помнить, что кодированные значения факторов соответствуют -1 нижнему уровню фактора, а +1 верхнему уровню фактора:
· для интенсивности поступления заявок λ нижний уровень равен λk=10![]() , а верхний λb=20
, а верхний λb=20![]() ;
;
· для интенсивности обслуживания μ нижний уровень равен μk=5![]() , а верхний 15 μb
, а верхний 15 μb![]() ;
;
· для количества мест в очереди L нижний уровень Lk =8и верхний Lb=12
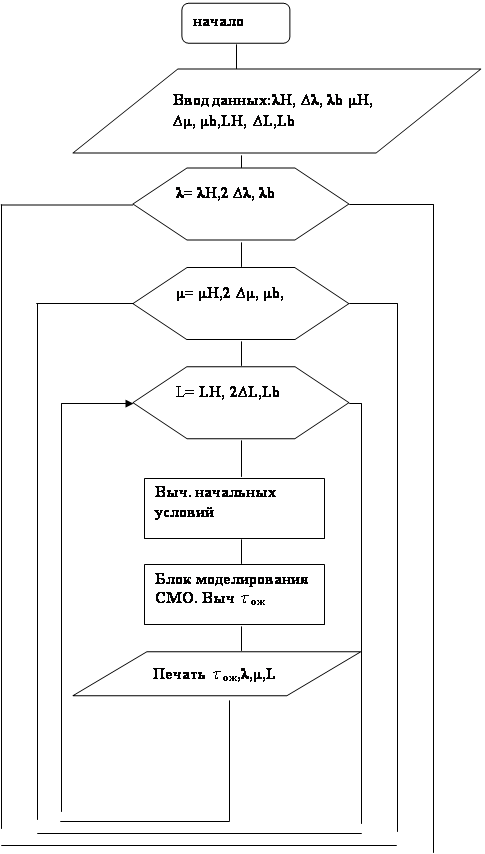
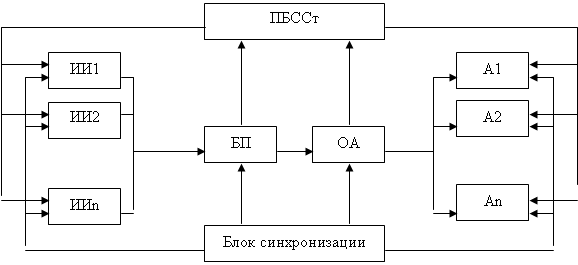
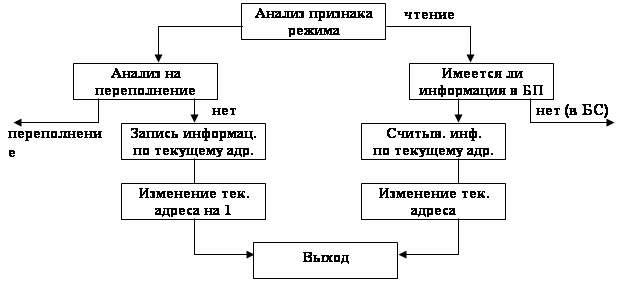
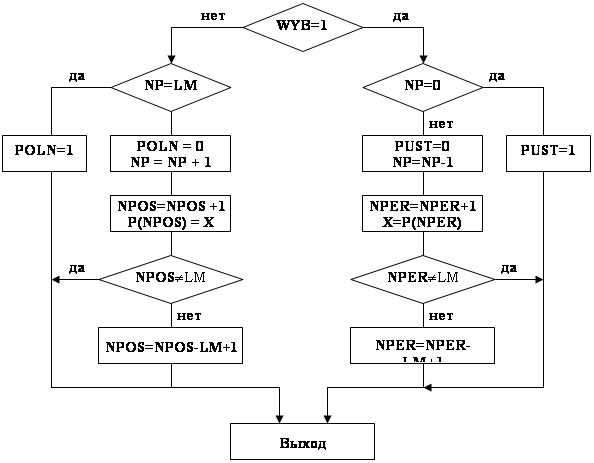
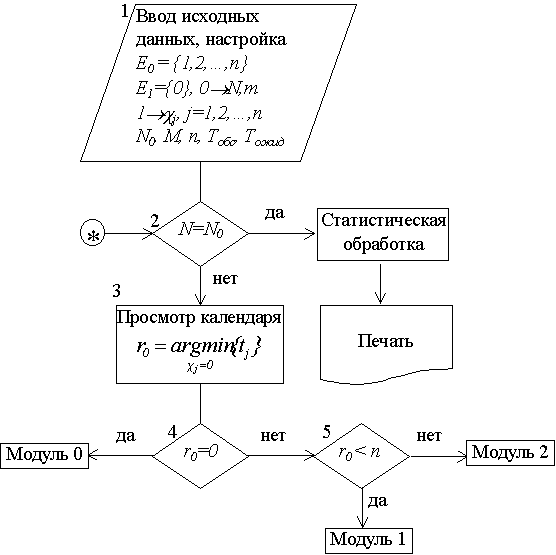
Поэтому при моделировании этих уровней факторов в блоке управления необходимо организовать их изменения. Это можно сделать путем введения нуля циклов. Тогда блок- схема управления вариантами моделирования примет вид (Рис1)
Рис1. Блок- схема управления вариантами моделирования
 | |||||
Для определения среднего времени ожидания ![]() ож можно воспользоваться блок- схемой Рис лабораторной работы 3. Результаты моделирования заносятся в Таблицу 2 в колонку для y.
ож можно воспользоваться блок- схемой Рис лабораторной работы 3. Результаты моделирования заносятся в Таблицу 2 в колонку для y.
По Таблице 2 и формуле 7 определяются коэффициенты выбранной модели планирования эксперимента аi (i=0.3). Таким образом, зависимость среднего времени ожидания от интенсивности поступления заявок, интенсивности обслуживания и количества мест в очереди примет вид:
![]() ож =…..λ+….μ+…L (10)
ож =…..λ+….μ+…L (10)
2. Содержание исследования
В состав исследования, проводимого в данной лабораторной работе, входит:
1. Анализ зависимости влияния экзогенных переменных модели однофазной одноканальной СМО на эндогенные переменные.
2. Построение плана машинного эксперимента на основе множественного регрессионного анализа и метода наименьших квадратов.
3.Моделирование системы массового обслуживания
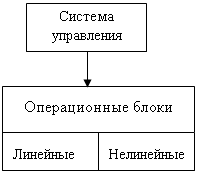
В качестве объекта моделирования рассматривается однофазная одноканальная система, структура, которой показана на Рис 2:
![]() μ
μ
очередь
![]()
![]()
![]()
![]() λ
λ

![]()

L
Рис2Структура исследуемой системы
Параметры системы:
· интенсивность поступления заявок λ=15![]() 5
5![]() ;
;
· интенсивность обслуживания μ=10![]() 5
5![]() ;
;
· длина очереди L=10![]() 2;
2;
Варианты лабораторной работы приведены в таблице 3, в которой ПФЭ полный факторный эксперимент; ДФЭ – дробный факторный эксперимент; ![]() ож - среднее время ожидания заявок в очереди;
ож - среднее время ожидания заявок в очереди; ![]() сист- среднее время пребывания заявок в системе;
сист- среднее время пребывания заявок в системе; ![]() - средняя длина очереди; Ротк – вероятность отказа; А – абсолютная пропускная способность системы; q- относительная пропускная способность системы; Кпр – коэффициент простоя системы.
- средняя длина очереди; Ротк – вероятность отказа; А – абсолютная пропускная способность системы; q- относительная пропускная способность системы; Кпр – коэффициент простоя системы.
4. Порядок выполнения работы
1. Ознакомится с методическими указаниями по выполнению данной лабораторной работы.
2. Получить у преподавателя вариант задания на составление плана машинного эксперимента для СМО
3. Составить матрицу планирования для проведения машинного эксперимента
4. Разработать блок- схему моделирующего алгоритма в соответствии с содержанием проводимого исследования
5. Составить программу на одном из языков программирования
6. Произвести отладку программы и решение поставленной задачи на ПЭВМ
7. Оформить отчет
Интерфейс программы
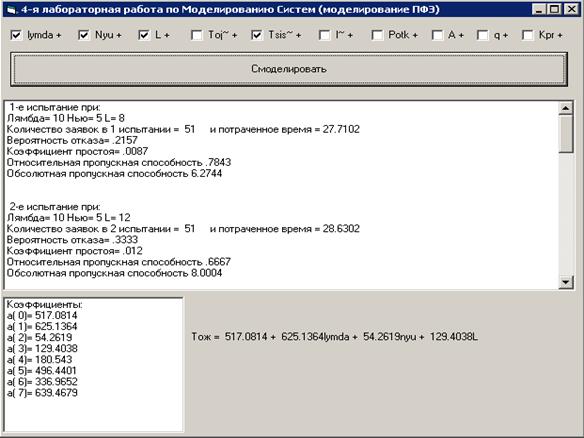
Листинг программы
Private Sub Command1_Click()
Dim L As Integer
Dim Tobs As Currency
Dim Tosv As Currency
Dim Toch() As Currency
Dim Potk As Currency
Dim q As Currency
Dim a(8) As Currency
Dim Kpr As Currency
List1.Clear
List2.Clear
List2.AddItem ("Коэффициенты:")
For lyamda = 10 To 20 Step 10
For nyu = 5 To 15 Step 10
For L = 8 To 12 Step 4
ReDim Toch(L) As Currency
x = 0.5
k = 0
Kotk = 0
Noch = 0
Toj = 0
Tsis = 0
Kobs = 0
Tnezan = 0
Tpost = 0
Tosv = 0
10: x = Rnd(x)
T = -1 / lyamda * Log(x)
Tpost = Tpost + T
k = k + 1
If k > 50 Then
GoTo 100
End If
30: If Tpost < Tosv Then
GoTo 20
Else
GoTo 40
End If
20: If Noch = L Then
Kotk = Kotk + 1
GoTo 10
Else
Noch = Noch + 1
Toch(Noch) = Tpost
GoTo 10
End If
40: If Noch = 0 Then
Kobs = Kobs + 1
Tnezan = Tpost - Tosv
x = Rnd(x)
Tobs = -1 / nyu * Log(x)
Tosv = Tpost + Tobs
Tsis = Tsis + Tobs
GoTo 10
Else
Voj = Tosv - Toch(1)
For i = 1 To Noch - 1
Toch(i) = Toch(i + 1)
Next i
Noch = Noch - 1
Toj = Toj + Voj
x = Rnd(x)
Tobs = -1 / nyu * Log(x)
Tsis = Tsis + Tobs + Voj
Tosv = Tosv + Tobs
Kobs = Kobs + 1
GoTo 30
End If
100: Kpr = Tnezan / Tsis
Potk = Kotk / k
q = 1 - Potk
Ab = q * L
j = j + 1
List1.AddItem (Str(j) + "-е испытание при:")
List1.AddItem ("Лямбда=" + Str(lyamda) + " Нью=" + Str(nyu) + " L=" + Str(L))
List1.AddItem ("Количество заявок в" + Str(j) + " испытании = " + Str(k) + " и потраченное время =" + Str(Tsis))
List1.AddItem ("Вероятность отказа=" + Str(Potk))
List1.AddItem ("Коэффициент простоя=" + Str(Kpr))
List1.AddItem ("Относительная пропускная способность" + Str(q))
List1.AddItem ("Обсолютная пропускная способность" + Str(Ab))
List1.AddItem ("")
List1.AddItem ("")
a(j) = (lyamda + nyu + L) * Toj
List2.AddItem ("a(" + Str(j - 1) + ")=" + Str(a(j)))
Next L
Next nyu
Next lyamda
Label1.Caption = "Tож = " + Str(a(1)) + " + " + Str(a(2)) + "lymda" + " + " + Str(a(3)) + "nyu" + " + " + Str(a(4)) + "L"
End Sub
Похожие работы
... системы осуществляется на этапе валидации. Валидация модели обычно выполняется на различных уровнях. Специальные методы валидации включают установление адекватности путем использования постоянных значений всех параметров имитационной модели или путем оценивания чувствительности выходов к изменению значений входных данных. В процессе валидации сравнение должно осуществляться на основе анализа как ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
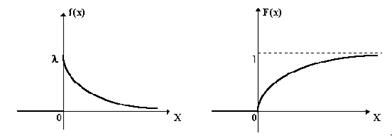
... из одного состояния в другое и распределение времени пребывания процесса в каждом состоянии (в виде функции распределения F(t) или в виде плотности распределения f(t)) Классификация систем массового обслуживания В общем случае СМО классифицируется по следующим признакам: · закону распределения входного потока · числу обслуживающих приборов · закону распределения времени обслуживания в ...
... и опасных факторов на человека при высокой производительности труда, создать комфортные условия для работы людей. Темой данной дипломной работы является методика оптимизации структуры и параметров библиотечной автоматизированной системы обеспечения информационными услугами. Работа проводилась на территории НТУ «ХПИ» в корпусе «У2». Рабочее помещение расположено на пятом этаже семиэтажного здания. ...
0 комментариев