Навигация
Порядок моделирования входного сигнала
ДОНБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра АУТПТЭК
КУРСОВАЯ РАБОТА
МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ В SIMULINK
По курсу “Компьютерная графика”
Алчевск, 2007
Содержание
Введение
1 Моделирование входных сигналов (моделирование объекта А)
1.1 Общие принципы представления сигналов математическими моделями
1.2 Моделирование сигнала заданного вида
2 Моделирование объекта Б
3 Моделирование объекта В
4 Моделирование системы
5 Анализ результатов моделирования
Выводы
Перечень ссылок
Введение
Моделирование различных систем, объектов, процессов, явлений природы и т.д. имеет важное значение в науке и технике. Благодаря моделированию существенно облегчается и удешевляется исследование физических, химических и других природных явлений, технических объектов, создание образцов новой техники. Моделированием называется создание моделей реальных объектов и их экспериментальные исследования. В свою очередь модель – это, как правило, упрощенное отражение реального объекта, несущее те его качества, которые подвергаются исследованию (моделированию).
Большое значение имеют, так же, математические модели. Они позволяют производить моделирование реальных объектов и систем с использованием многочисленных математических методов, оперируя со свойствами объектов, выраженными в виде различных математических зависимостей и соотношений. Математические модели той или иной степени сложности, как правило, идеализированы и отражают только исследуемые характеристики реальных объектов.
С математическими моделями тесно связаны компьютерные модели, которые в зависимости от программы в которой производится моделирование, используют те или иные математические характеристики реальных объектов. В настоящее время в связи со значительным прогрессом в области компьютерной техники компьютерное моделирование приобрело большое значение в науке и технике. На сегодняшний день существует значительное количество специализированных пакетов, таких как MatLab, MathCad, Math, Mathematica, Maple и др., которые дают широкие возможности для компьютерного моделирования различных процессов и систем.
Целью данной курсовой работы является изучение принципов решения различных технических задач с использованием компьютерной техники и приобретение практических навыков моделирования процессов и объектов.
В результате выполнения курсовой работы необходимо изучить принципы построения моделей в программе Simulink, освоить методику моделирования в ней и расширить знания и навыки при решении математических задач (к которым сводится большинство практических задач науки и техники) в пакете MatLab в целом. Необходимо, также, научиться строить графические зависимости различных функций, работать с табличными данными, конвертировать таблицы и графики в текстовый редактор Word и оформлять текстовые документы, включающие в себя формулы, таблицы, графические объекты.
1. Моделирование входного сигнала
1.1 Общие принципы представления сигналов математическими моделями
Входной сигнал может задаваться различными математическими моделями: динамическим представлением, геометрическим, спектральным, энергетическим. Динамическое представление произвольного сигнала с использованием функции Хевисайда:
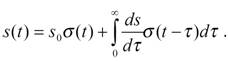
(1.1)
При геометрическом представлении вводится понятие координатного базиса: если совокупность векторов (e1, e2, еЗ,...) является линейно независимой, то она образует координатный базис в линейном пространстве. Тогда сигнал s(t) можно представить в виде
![]()
(1.2)
где числа (c1, c2, сЗ,...) являются проекциями сигнала s(t) относительно выбранного базиса.
При спектральном представлении сигнал s(t) и его спектральная плотность S(ω) взаимно-однозначно связаны прямым и обратным преобразованиями Фурье:
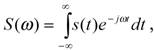
(1.3)
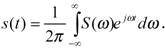
(1.4)
1.2 Моделирование сигнала заданного вида
Необходимо промоделировать сигнал, представляющий собой
произведение двух функций: X=X4*X16; X(t)=X4*X16
Сигнал X4 задан функцией вида:
![]() (1.5)
(1.5)
где A = 40, T=4ms, ![]()
Для перехода к циклической частота воспользуемся формулой:
![]() ;
; ![]() ; (1.6)
; (1.6)
![]() рад/с
рад/с
Сигнал X16 задан функцией вида:
![]() (1.7)
(1.7)
где A = 75, T=17ms, ![]()
Для перехода к циклической частоте воспользуемся формулой (1.6):
![]() ;
;
![]() рад/с
рад/с
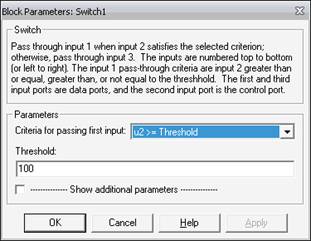
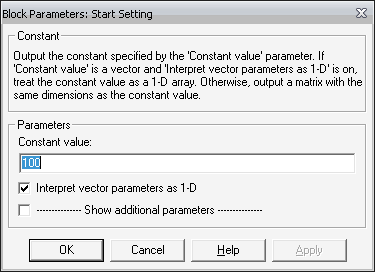
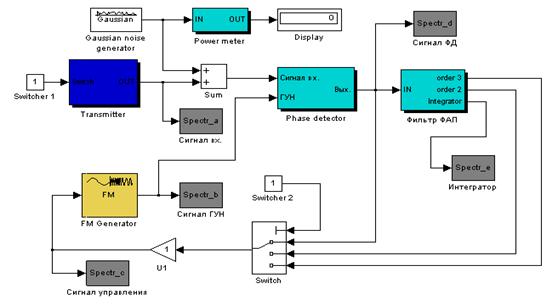
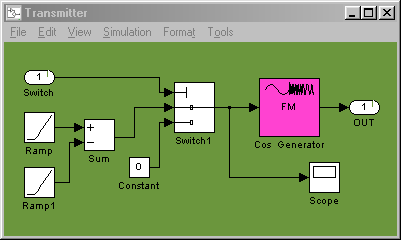
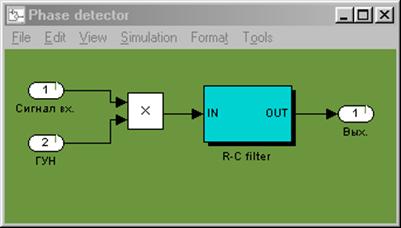
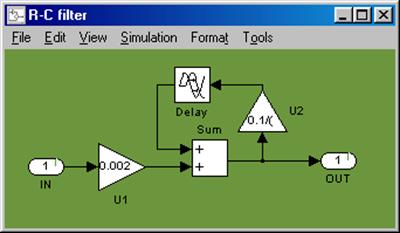
После преобразований составим структурную схему в Simulink для моделирования заданных сигналов, а так же для моделирования результирующего сигнала. Она приведена на рисунке 1.1.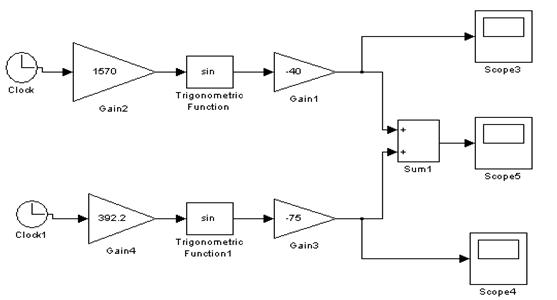
Рисунок 1.1– Структурная схема для моделирования сигнала 1, 2 и результирующего сигнала
|
|
|
Объект Б задан дифференциальным уравнением:
2.88y///+ 5.76 y// + 5.76 y/ +2.88y = 9.23x (2.1)
Преобразуем дифференциальное уравнение (2.1) к машинному виду
2.88p3y(p) + 5.76 p2y(p) + 5.76 py(p) +2.88y(p) = 9.23x(p) (2.2)
y(p)(2.88p3 + 5.76 p2 + 5.76 p +2.88) = 9.23x(p) (2.3)
Так как правая часть уравнения (2.1) не содержит производной от входного сигнала, решим его общим методом. Запишем его в форме Коши:
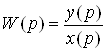 ; (2.4)
; (2.4)
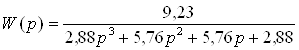 (2.5)
(2.5)
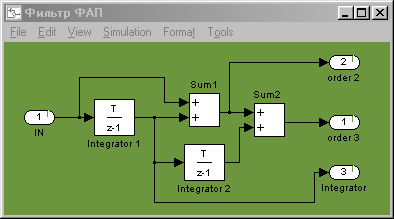
Полученное уравнение позволяет осуществить построение двух структурных схем для моделирования объекта, заданного уравнением (2.1). Структурные схемы приведены на рисунке 2.1 и 2.2

Рисунок 2.1 – Структурная схема модели объекта Б (с использованием блока Transfer Fcn)
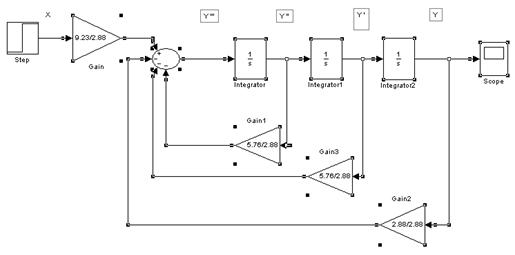
Рисунок 2.2 – Структурная схема модели объекта Б (с использованием блоков Integrator)
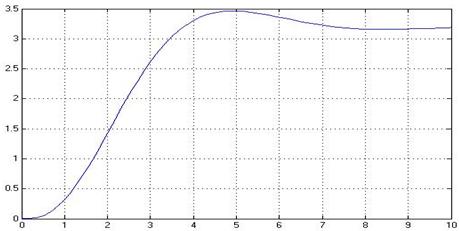
Для оценки параметров объекта Б строится переходная характеристика, которая является реакцией исследуемой системы на функцию включения (функцию Хевисайда). Графики переходных характеристик приведены на рисунках 2.3 и 2.4 (с использованием блоков Transfer Fcn и Integrator соответственно)
|
|
Рисунок 2.3 – График структурной схемы модели объекта Б (с использованием блока Transfer Fcn)
|
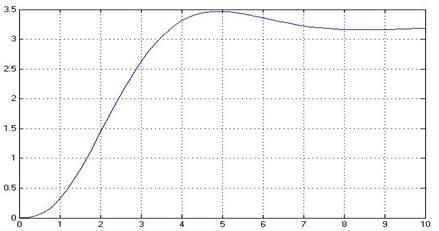
Рисунок 2.4 – График структурной схемы модели объекта Б (с использованием блоков Integrator)
Как и следовало ожидать график, построенный с помощью блока Transfer Fcn и график, построенный с помощью блоков Integrator идентичны.
Похожие работы
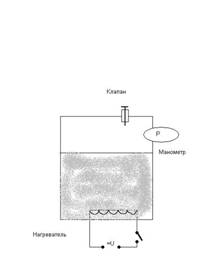
... ПИ- и ПИД-регуляторов при использовании метода Циглера - Николса, а на рис. 51 показан график регулируемой величины в режиме автоколебаний. Рис.2 Применение ПИД-регулятора на примере моделирования автоклава При стерилизации (пастеризации) должен строго соблюдаться установленный технологической инструкцией режим (температура, продолжительность и давление при стерилизации, пастеризации) с ...
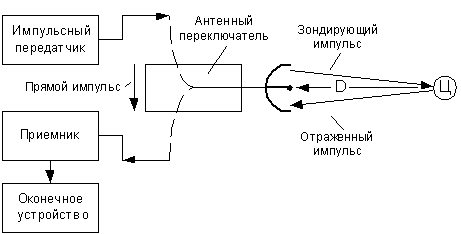
... = arcsin (Δfн/ SуE). Для систем ФАП большего порядка полосы удержания и захвата не равны друг другу. Элементы теории систем фазового регулирования. Система фазовой автоподстройки частоты Система фазовой автоподстройки частоты состоит из трех основных элементов: перемножителя, инвариантного во времени линейного фильтра и управляемого генератора, рис. П.2.1. Представим входной сигнал ...
... на разработку и материальные затраты. Таким образом, цель дипломного проектирования – разработка программного комплекса для моделирования радиолокационной обстановки на персональном компьютере, позволяющего моделировать радиолокационную обстановку по заданным параметрам, создавать выходной файл, содержащий рассчитанную модель, использовать полученный файл для проверки реальных устройств обработки ...
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...




0 комментариев