Навигация
3 Моделирование объекта В
Объект В задан структурной схемой представленной на рисунке 3.1:
![]() Х(Р)
Х(Р)![]()
![]()
|
|
Рисунок 3.1 – Структурная схема объекта В
W1э = W4*W10 (3.1)
W1э = W4(p)*W10(p);
![]()
![]() (3.2)
(3.2)
Элементы схемы соединены последовательно:
W4 + W10 = ![]() *
* ![]() (3.3)
(3.3)
Параметры объекта:
T1 = 0.1c; T2 = 1.1;T3 = 0.9c.
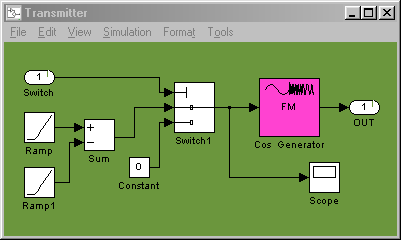
Для оценки параметров объекта В строится переходная характеристика, которая является реакцией исследуемой системы на функцию включения (функцию Хевисайда). Структурная схема модели объекта В приведена на рисунке 3.2 а его график переходной характеристики приведен на рисунке 3.3.

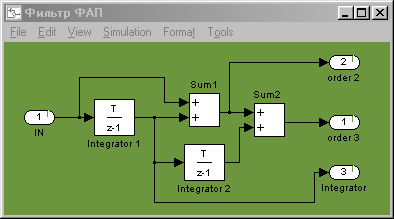
Рисунок 3.2 – Структурная схема модели объекта В
|
|
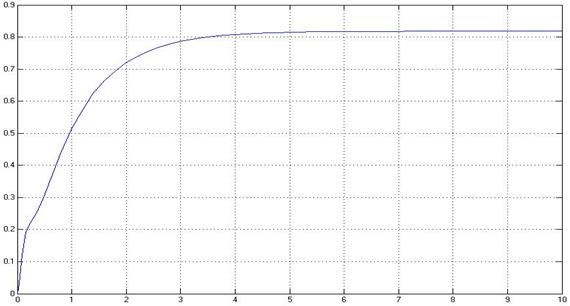
Рисунок 3.3 – График структурной схемы модели объекта В
4. Моделирование системы
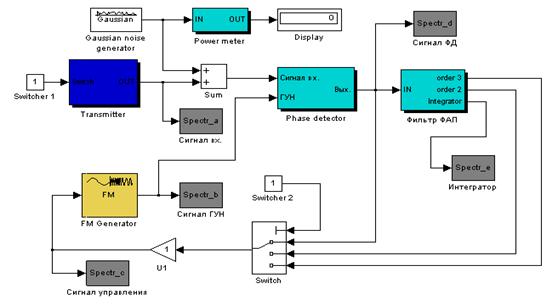
Структурная схема системы, приведенная на рисунке 4.1, представляет собой последовательное соединение, состоящее из смоделированных ранее структур объекта Б (с использованием блока Transfer Fcn) и объекта В. Она приведена на рисунке 4.1.
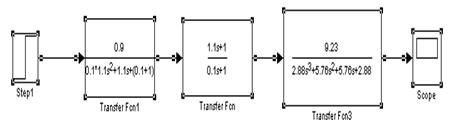
Рисунок 4.1 – Схема общей структуры системы
В соответствии со структурной схемой сигнал подается на объект Б и объект В. Реакцией синтезируемой системы на единичный скачок будет являться переходный процесс, график которого представлен на рисунке 4.2.
![]()
|
|
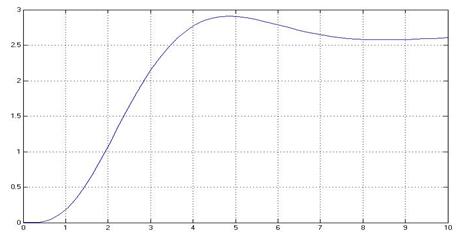
Рисунок 4.2 – График структурной схемы модели объекта В
5. Анализ результатов моделирования
В процессе моделирования заданных сигналов X15 и X3 разработана структурная схема (рисунок 1.1) и получены функции, представленные на рисунках 1.2. 1.3. 1.4..
Объект Б задан дифференциальным уравнением (2.1) и имеет третий порядок. Для оценки параметров объекта Б строится переходная характеристика, которая является откликом исследуемой системы на функцию включения (функцию Хевисайда). График переходной характеристики приведен на рисунке 2.3 и 2.4. Она имеет колебательный характер.
Объект В задан суммой передаточных функций (3.3) первого порядка. Для оценки параметров объекта В строится переходная характеристика, которая является откликом исследуемой системы на функцию включения (функцию Хевисайда). График переходной характеристики приведен на рисунке 3.3. Она имеет апериодический характер.
Функция, приведенная на рисунке 4.1 является системой смоделированных ранее структуры объекта Б (с использованием блока Transfer Fcn) и объекта В. Откликом системы на данное воздействие является функция, график которой приведен на рисунке 4.2.
Выводы
В результате выполнения курсовой работы были получены следующие результаты.
Смоделированы сигналы X15, X3 а так же X15 + X3 графики которых приведены на рисунках 1.2, 1.3 и 1.4 соответственно.
Построена структурная схема объекта Б заданного дифференциальным уравнением (рис. 2.1). Произведено ее моделирование и получена переходная характеристика (рис. 2.3 и 2.4).
Объект Б был задан суммой передаточных функций (3.1). Переходная характеристика объекта Б показана на рис. 3.1.
В процессе работы над курсовым проектом я узнал много нового и интересного. Были закреплены знания и навыки, полученные в курсах КГ, КТ и ОВР.
Полученные знания и навыки будут использоваться мною в дальнейшем при изучении других дисциплин, написании курсовых проектов и дипломной работы, а также в моей будущей инженерной и научной деятельности.
Перечень ссылок
1. И.В.Черных. Simulink: Инструмент моделирования динамических систем. – M.:Exponenta. 2000
2. Потемкин В.Г. Система инженерных и научных расчетов MATLAB 5.x: в 2-х томах. Том 1. - М.: ДИАЛОГ МИФИ. 1999. – 366 с.
3. Гультяев А.К. MATLAB 5.2. Имитационное моделирование в среде Windows: Практическое пособие. - СПб.: КОРОНА принт, 1999. – 288 с.
4. Теория систем автоматического регулирования, издание третье, исправленное. Бесекерский В.А., Попов Е.П. М.: Наука. 1975, 768 с.
5. Воронов А.А. Основы теории автоматического регулирования. Часть 1. М–Л: Энергия. 1965. 396 с.
6. Луценко В.А.. Финякин Л.Н. Математическое моделирование химико-технологических процессов на АВМ. – М.: Химия. 1978.
7. Горбацевич Е.Д. Левинзон Ф.Ф. Аналоговое моделирование систем управления. – М.: Наука. Главная редакция физико – математической литературы. 1984. – 304 с.
8. Левин В.И., Гросберг Ю.И. Дифференциальные уравнения математической физики. – М.: Гостехиздат. 1951.
9. Гельман В.Я. Практикум по математике на компьютере. СПб: СПИГ. 2001.
10. Мякинный О.A. Mikrosoft Word 2003: Самоучитель / О.А. Мякинный. - М: Диалектика. 2004. - 272 с.
Похожие работы
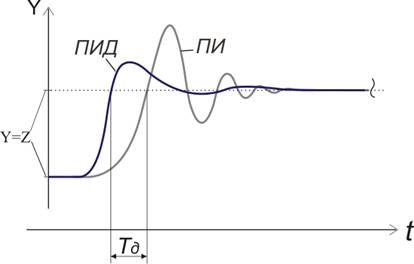
... ПИ- и ПИД-регуляторов при использовании метода Циглера - Николса, а на рис. 51 показан график регулируемой величины в режиме автоколебаний. Рис.2 Применение ПИД-регулятора на примере моделирования автоклава При стерилизации (пастеризации) должен строго соблюдаться установленный технологической инструкцией режим (температура, продолжительность и давление при стерилизации, пастеризации) с ...
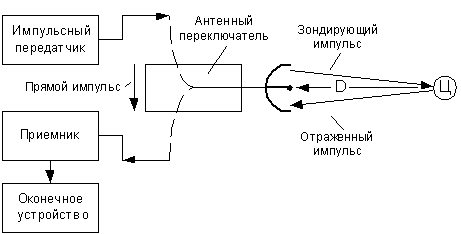
... = arcsin (Δfн/ SуE). Для систем ФАП большего порядка полосы удержания и захвата не равны друг другу. Элементы теории систем фазового регулирования. Система фазовой автоподстройки частоты Система фазовой автоподстройки частоты состоит из трех основных элементов: перемножителя, инвариантного во времени линейного фильтра и управляемого генератора, рис. П.2.1. Представим входной сигнал ...
... на разработку и материальные затраты. Таким образом, цель дипломного проектирования – разработка программного комплекса для моделирования радиолокационной обстановки на персональном компьютере, позволяющего моделировать радиолокационную обстановку по заданным параметрам, создавать выходной файл, содержащий рассчитанную модель, использовать полученный файл для проверки реальных устройств обработки ...
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...



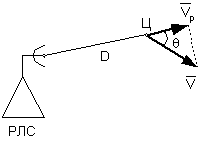

0 комментариев