Навигация
Решение задачи аналитическим методом
4.3 Решение задачи аналитическим методом
Полагая k=0, по известному алгоритму составим опорное решение методом Фогеля. Полученный опорный план перевозок и алгоритм выполнения с нахождением минимальных разностей стоимостей перевозок (Cij) в каждом столбце и строке изображен на рисунке 4.3.1.
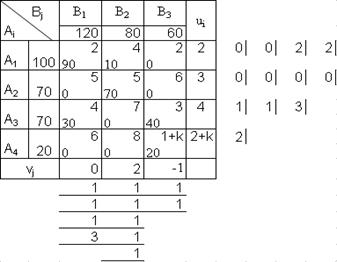
Рис. 4.3.1. Составление первого опорного решения задачи по методу Фогеля
Процесс выполнения получения опорного решения с последовательным назначением перевозок в ячейки: А4В3 - А3В3 - А3В1 - А1В1 - А1В2 - A2B2.
Проверка плана на вырожденность: m+n-1=6. План невырожденный.
Проверим опорное решение на оптимальность по методу потенциалов. Расчет потенциалов строк и столбцов для занятых из условия vi + uj = cij для занятых клеток и проверка условия vi + uj ≤ cij для незанятых приведены в таблице 4.3.1.
Решение, полученное при k=0, является оптимальным для всех значений параметра k, удовлетворяющих условию ![]() .
.
Из условия для свободных клеток найдем:
∆13 = v3 + u1 - c'13 = -1 + 2 - 2 = -1
∆21 = v1 + u2 - c'21 = 0 + 3 - 5 = -2
∆23 = v3 + u2 - c'23 = -1 + 3 - 6 = -4
∆32 = v2 + u3 - c'32 = 2 + 4 - 7 = -1
∆41 = v1 + u4 - c'41 = 0 + 2+k - 6 = -4 + k
∆42 = v2 + u4 - c'42 = 2 + 2+k - 8 = -4 + k
Табл. 4.3.1. Проверка первого опорного решения на оптимальность методом потенциалов
| заполненные | незаполненные | ||||
| № | vi + uj = cij | значения | № | vi + uj ≤ cij | условие |
| А1В1 | v1+u1=2 | v1=0, u1=2 | А1В3 | v3+u1<=2 | соблюдается |
| А1В2 | v2+u1=4 | v2=2 | А2В1 | v1+u2<=5 | соблюдается |
| A2B2 | v2+u2=5 | u2=3 | А2В3 | v3+u2<=6 | соблюдается |
| A3B1 | v1+u3=4 | u3=4 | А3В2 | v2+u3<=7 | соблюдается |
| A3B3 | v3+u3=3 | v3= -1 | A4B1 | v1+u4<=6 | соблюдается |
| A4B3 | v3+u4=1+k | u4=2+k | A4B2 | v2+u4<=8 | соблюдается |
Определение значений k1 и k2:
k1 = max(-aij/Bij) = ![]() т.к.
все Bij ≥ 0
т.к.
все Bij ≥ 0
k2 = min(-aij/Bij) = (-a41/B41; -a42/B42) = min(4;4) = 4. Все Bij > 0.
Так как по условию задачи k≥0, то оптимальное решение сохраняется при 0≥k≥4.
При этом минимальная стоимость транспортных расходов составляет:
F(X1)min = 20*(1+k) + 40*3 + 30*4 + 90*2 + 10*4 + 70*5 = 830 + 20k
Таким образом, при ![]() , F(X1)min = 830 + 20k и
, F(X1)min = 830 + 20k и
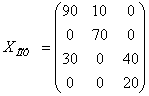 .
.
Чтобы получить оптимальное решение при k≥4 перераспределим поставки товаров в клетку (4,1), где k2=4. Вновь полученное распределение с учетом изменения стоимости перевозки в ячейке A4B3 (k=4) представлено на рисунке 4.3.2.
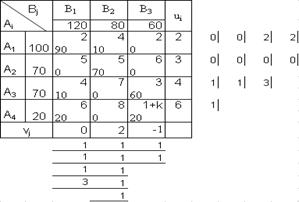
Рис. 4.3.2. Составление второго опорного решения задачи по методу Фогеля
Процесс выполнения получения опорного решения с последовательным назначением перевозок в ячейки: А4В1 - А3В3 - А3В1 - А1В1 - А1В2 - A2B2.
Проверка плана на вырожденность: m+n-1=6. План невырожденный.
Проверим опорное решение на оптимальность по методу потенциалов. Расчет потенциалов строк и столбцов для занятых из условия vi + uj = cij для занятых клеток и проверка условия vi + uj ≤ cij для незанятых приведены в таблице 4.3.2.
Табл. 4.3.2 Проверка второго опорного решения на оптимальность методом потенциалов
| заполненные | незаполненные | ||||
| № | vi + uj = cij | значения | № | vi + uj ≤ cij | условие |
| А1В1 | v1+u1=2 | v1=0, u1=2 | А1В3 | v3+u1<=2 | соблюдается |
| А1В2 | v2+u1=4 | v2=2 | А2В1 | v1+u2<=5 | соблюдается |
| A2B2 | v2+u2=5 | u2=3 | А2В3 | v3+u2<=6 | соблюдается |
| A3B1 | v1+u3=4 | u3=4 | А3В2 | v2+u3<=7 | соблюдается |
| A3B3 | v3+u3=3 | v3= -1 | A4B2 | v2+u4<=8 | соблюдается |
| A4B1 | v1+u4=6 | u4=6 | A4B3 | v3+u4<=1+k | соблюдается |
Решение, полученное при k=4, является оптимальным для всех значений параметра k, удовлетворяющих условию ![]() .
.
Из условия для свободных клеток найдем:
∆13 = a3 + b1 - C'13 = -1 + 2 - 2 = -1
∆21 = a1 + b2 - C'21 = 0 + 3 - 5 = -2
∆23 = a3 + b2 - C'23 = -1 + 3 - 6 = -4
∆32 = a2 + b3 - C'32 = 2 + 4 - 7 = -1
∆42 = a2 + b4 - C'42 = 2 + 6 - 8 = 0
∆43 = a3 + b4 - (C'43 + С''43) = -1 + 6 - (1+k) = 4-k
Определение значений k1 и k2
k1 = max(-aij/Bij) = -a43/B43 = 4. Все Bij < 0
k2 = min(-aij/Bij) = ![]() т.к. все Bij ≤ 0
т.к. все Bij ≤ 0
Так как по условию задачи k ≤ 9, то оптимальное решение сохраняется при 4≥k≥9.
При этом минимальная стоимость транспортных расходов составит:
F(X2)min = 20*6 + 60*3 + 10*4 + 90*2 + 10*4 + 70*5 = 910
Таким образом, при ![]() F(X2)min = 910 и
F(X2)min = 910 и
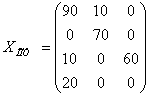 .
.
Похожие работы
... с организации экспортного отдела и заканчивают созданием международного филиала. Однако некоторые идут дальше и превращаются в транснациональные компании, высшее руководство которых уже занимается планированием маркетинга и его управлением во всемирном масштабе. Фирмы США расширяют свою международную деятельность и ищут людей, относительно свободно владеющих тем или иным иностранным языком, ...
... себя почти все методы оценки издержек и экономических выгод, а также относительной рентабельности деятельности предприятия. Типичная «экономическая» модель основана на анализе безубыточности, методе принятия решений с определением точки, в которой общий доход уравнивается с суммарными издержками, т.е. точки, в которой предприятие становится прибыльным. Эти модели широко применяются в бухгалтерском ...
... , 6) сетевого планирования и управления, 7) выбора маршрута, 8) комбинированные. Из перечисленных выше методов математического программирования наиболее развитым и законченным является линейное программирование. В его рамки укладывается широкий круг задач исследования операций. Линейное программирование Несмотря на требование линейности целевой функции и ограничений, в рамки линейного ...
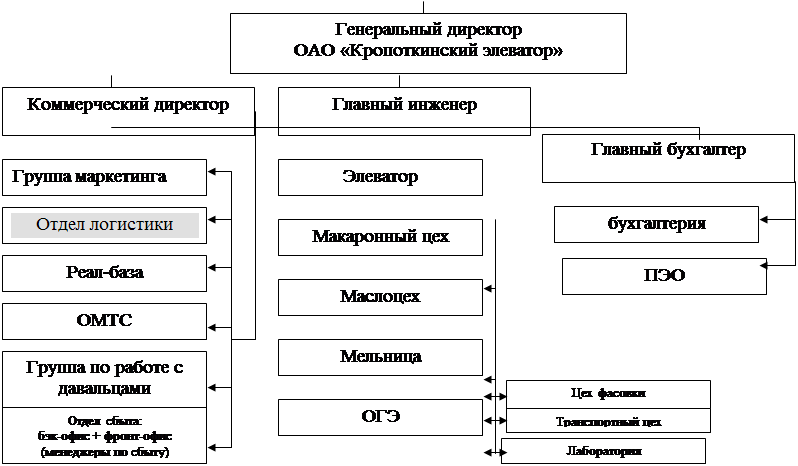
... что по аналогии с использованием других ресурсов должен быть создан эффективный механизм управления им на базе единых стандартов информационного обеспечения. Таким образом, повышение эффективности логистических транспортных потоков в первую очередь зависит от формирования системы их информационным обеспечением. Внедрение рассмотренной выше методики позволит ОАО «Кропоткинский элеватор» - более ...


0 комментариев