Навигация
Решение задачи средствами Ms Excel
22826
знаков
6
таблиц
12
изображений
4.4 Решение задачи средствами Ms Excel
Создадим в окне программы Ms Excel две матрицы «План перевозок» и «Стоимость перевозок», согласно вышеизложенным правилам (рис 4.4.1). Также нужно указать ячейку содержащую изменяемый параметр k. При этом в клетке A4B3 матрицы «Стоимость перевозок» устанавливаем формулу, отображающую зависимость данного тарифа от параметра k: L7=1+L9.
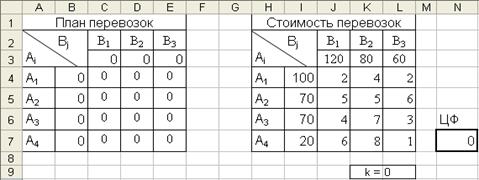
Рис. 4.4.1. Фрагмент окна программы Ms Excel: Матрицы «План перевозок» и «Стоимость перевозок» с изменяемым тарифом C43.
В ячейки, которые должны отображать запасы поставщиков и потребности потребителей в матрице «План перевозок» вводим формулы суммирующие значения всех возможных поставок данных поставщиков и потребителей, например: B4=СУММ(C4:E4), C3=СУММ(С4:С7).
В ячейку целевой функции (N7) введем =СУММПРОИЗВ(C4:E7;J4:L7).
Метод решения параметрической транспортной задачи средствами Ms Excel заключается в нахождении оптимального решения при каждом значении параметра k, с сохранением сценария для каждой процедуры «Поиск решения». После этого необходимо из всего диапазона изменения параметра k выделить отдельные промежутки, на которых сохраняется оптимальное решение задачи и минимальная стоимость затрат.
В диалоговом окне «Поиск решения», согласно вышеуказанным правилам установим все необходимые ограничения и ссылки на необходимые ячейки (рис. 4.4.2). Также необходимо в ограничениях указать пределы изменения параметра k, т.е. 0≤k≤9.
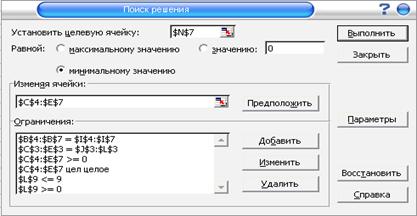
Рис. 4.4.2. Диалоговое окно «Поиск решения»
В диалоговом окне «Параметры поиска решения» установить необходимые параметры (рис. 4.4.3).
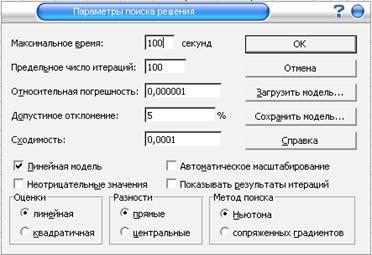
Рис. 4.4.3. Диалоговое окно «Параметры поиска решения»
После нажатия на кнопку «Выполнить» в диалоговом окне «Результаты поиска решения» (рис. 4.4.5) нажать «Сохранить сценарий…» и в появившемся диалоговом окне «Сохранение сценария» задать имя данному сценарию и нажать «ОК» (рис. 4.4.4.).
Рис. 4.4.4. Диалоговое окно «Сохранение сценария»
После сохранения сценария в диалоговом окне «Результаты поиска решения» выделить необходимые типы отчетов и нажать «OK» (рис. 4.4.5.).
Рис. 4.4.5. Диалоговое окно «Результаты поиска решений
После выполнения всех операций в матрице «План перевозок» получим оптимальный план перевозок при k=0 (рис. 4.4.6.).
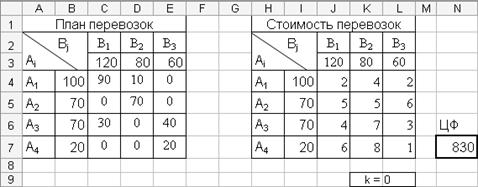
Рис. 4.4.6. Фрагмент окна программы Ms Excel: Результат поиска решения при k=0.
Полученное значение целевой функции F(x1)min=830.
Теперь аналогичным способом найдем оптимальный план перевозок при k=1. Проведя повторный расчет, получим новый план перевозок и значение целевой функции (рис 4.4.7.).
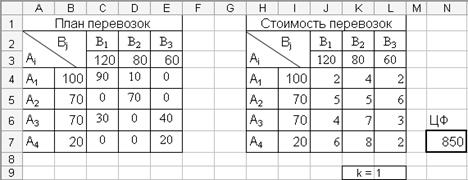
Рис. 4.4.7. Фрагмент окна программы Ms Excel: Результат поиска решения при k=1
Полученное значение целевой функции F(x2)min = 850.
Как видно из рисунков 4.4.5. и 4.4.6 планы перевозок в обоих случаях (k=0, k=1) одинаковы. После дальнейших расчетов при всех остальных значениях параметра k обнаружим, что при 
план перевозок остается неизменным, изменяется лишь значение целевой функции. При значении параметра 
«Поиск решения» выдает другой план перевозок, и значение целевой функции на данном промежутке остается неизменным F(x)min = 910. Полученный план перевозок при значении k=4 изображен на рисунке 4.4.8.
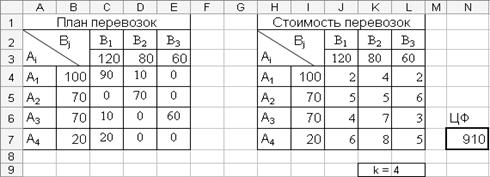
Рис. 4.4.8. Фрагмент окна программы Ms Excel: Результат поиска решения при k=4
Значения целевой функции, соответствующие параметру k в каждой итерации представлены в таблице 4.4.1.
Из представленных в таблице 4.4.1 данных можно вывести определенную закономерность изменения значения целевой функции на промежутке :
F(x1)min = 830, (k=0);
F(x2)min = F(x1)min +20 = 830+20, (k=1);
F(x3)min = F(x2)min +20 = 830 + 20*2 = 870, (k=2).
Следуя по той же цепочке, найдем:
F(x4)min = 830 + 20*3, (k=3).
F(x5)min = 830 + 20*4, (k=4).
Исходя из подобной логики можно представить F(x1)min = 830 + 20*0.
Отсюда можно вывести формулу, отображающую закономерность изменения значения целевой функции при :
.
Для значений значение функции постоянно F(x)=910.
Таблица 4.4.1. Значения целевой функции в каждой итерации
| номер итерации i | значение параметра ki | значение функции F(xi)min |
| 1 | 0 | 830 |
| 2 | 1 | 850 |
| 3 | 2 | 870 |
| 4 | 3 | 890 |
| 5 | 4 | 910 |
| 6 | 5 | 910 |
| 7 | 6 | 910 |
| 8 | 7 | 910 |
| 9 | 8 | 910 |
| 10 | 9 | 910 |
Команда «Сервис → Сценарии» открывает диалоговое окно «Диспетчер сценариев», которое отображает сохраненные сценарии каждой итерации нахождения оптимального плана перевозок (рис 4.4.9.).
Рис. 4.4.9. Диалоговое окно «Диспетчер сценариев»
С помощью «Диспетчера сценариев» можно просмотреть план перевозок и значение целевой функции, получаемые при каждом значении параметра k. Также можно просмотреть отчет, отображающий значения изменяемых ячеек в каждой из итераций.
Заключение
Ответ.
, 
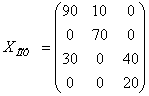, F(X1)min = 830 + 20k.
, 
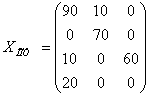, F(X2)min = 910.
Представленная в данной курсовой работе параметрическая транспортная задача решена двумя способами: аналитическим методом Фогеля и средствами компьютерной программы Ms Excel. Оба предложенных метода дают одинаковое решение и определяют оптимальный план перевозок товара и минимальную стоимость всех перевозок для каждого из промежутков диапазона изменения параметра, определяющего тариф одной из перевозок.
Описанная в работе задача об оптимальных перевозках и методы ее решения – только отдельный пример огромного множества задач линейного программирования. Цель транспортной задачи – разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок. Все это сокращает время продвижения товаров, уменьшает затраты предприятий, фирм, связанные с осуществлением процессов снабжения сырьем, материалами, топливом, оборудованием и т.д.
Библиографический список
1. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом анализе: Учебник. – 3-е изд., исп. – М.: Дело, 2002. – 688 с.
2. И.Л. Акулич. Математическое программирование в примерах и задачах: учебное пособие для ВУЗов. - М.: Высшая школа, 1986 г, 319 с.
3. Т.Н. Павлова, О.А. Ракова. Линейное программирование. Учебное пособие. - Димитровград, 2002 г.
4. Т.Н. Павлова, О.А. Ракова. Решение задач линейного программирования средствами Excel. Учебное пособие. - Димитровград, 2002 г.
5. В.И. Ермаков. Сборник задач по высшей математике для экономистов. - М.: Издательство Инфра, 2001 г, 574 с.
Похожие работы
... с организации экспортного отдела и заканчивают созданием международного филиала. Однако некоторые идут дальше и превращаются в транснациональные компании, высшее руководство которых уже занимается планированием маркетинга и его управлением во всемирном масштабе. Фирмы США расширяют свою международную деятельность и ищут людей, относительно свободно владеющих тем или иным иностранным языком, ...
... себя почти все методы оценки издержек и экономических выгод, а также относительной рентабельности деятельности предприятия. Типичная «экономическая» модель основана на анализе безубыточности, методе принятия решений с определением точки, в которой общий доход уравнивается с суммарными издержками, т.е. точки, в которой предприятие становится прибыльным. Эти модели широко применяются в бухгалтерском ...
... , 6) сетевого планирования и управления, 7) выбора маршрута, 8) комбинированные. Из перечисленных выше методов математического программирования наиболее развитым и законченным является линейное программирование. В его рамки укладывается широкий круг задач исследования операций. Линейное программирование Несмотря на требование линейности целевой функции и ограничений, в рамки линейного ...
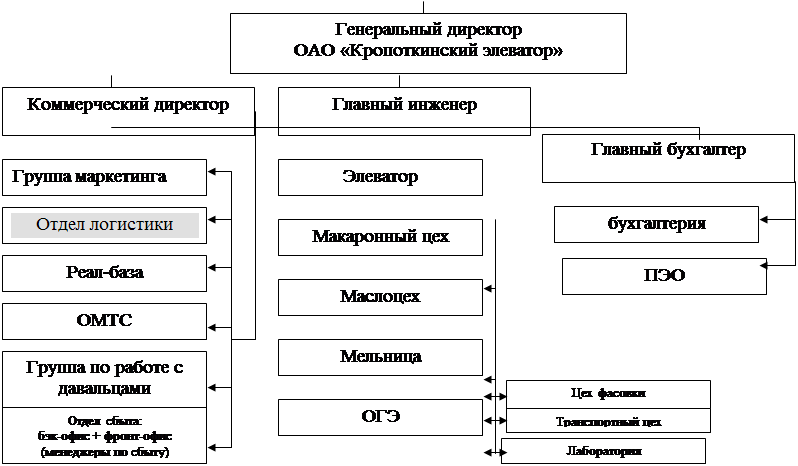
... что по аналогии с использованием других ресурсов должен быть создан эффективный механизм управления им на базе единых стандартов информационного обеспечения. Таким образом, повышение эффективности логистических транспортных потоков в первую очередь зависит от формирования системы их информационным обеспечением. Внедрение рассмотренной выше методики позволит ОАО «Кропоткинский элеватор» - более ...
0 комментариев