Навигация
Инструкция по инсталляции программного продукта
4. Инструкция по инсталляции программного продукта
Для установки программы запустите файл GRAPHICv1.0\setup.exe и следуйте инструкциям мастера. Для удаления программы можно воспользоваться этим же файлом.
Гарантируется работа данной программы в операционной системе Windows не ниже 98. В предыдущих версиях работа программы не проверялась.
Установка программы требует около 1 Мб свободной памяти на жестком диске.
Внимание!
За возможные ошибки, сбои, возможный причиненный моральный или материальный ущерб и т.д., авторы ответственности не несут. Вы используете программу на свой страх и риск!
Если вы не согласны с этим, то не используйте данную программу!
5. Инструкция оператору
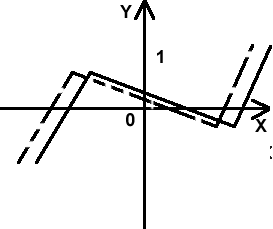
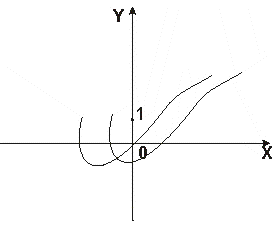
При открытии программы появляется окно, в котором уже по умолчанию построен график функции f(x)=sin(x)+0.05*x на отрезке [-5,10], как показано на рисунке:
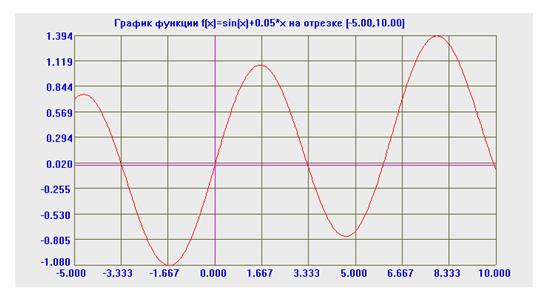
Чтобы построить необходимый график функции или изменить отрезок, на котором построен график, выберите на панели меню пункт Функция. При этом появится такое диалоговое окно:
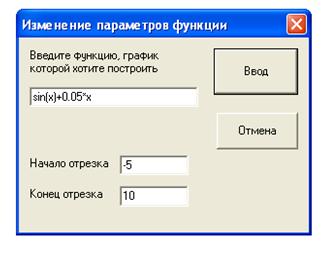
В этом окне вы можете изменять параметры функции. Начало и конец отрезка могут быть введены любые из отрезка [-1.7976931348623158e+308, 1.7976931348623158e+308], но при этом начало должно быть меньше конца отрезка, иначе появится сообщение об ошибке.
С функцией дело немного сложнее. Чтобы интерпретатор правильно понял функцию, при её вводе нужно пользоваться правилами.
Унарные операции:
cos(x) - косинус
sin(x) - синус
tg(x) = tan(x) - тангенс
ctg(x) - котангенс
arccos(x) = acos(x) - арккосинус
arcsin(x) = asin(x) - арксинус
arctg(x) = atan(x) - арктангенс
arcctg(x) - арккотангенс
round(x) - обычное округление до целого
sqr(x) - квадрат
sqrt(x) - арифметический корень
abs(x) = fabs(x) - модуль
neg(x) - отрицание
fact(x) - факториал
exp(x) - экспонента
ln(x) - натуральный логарифм
log10(x) = lg(x) - десятичный логарифм
cosh(x) - гиперболический косинус
sinh(x) - гиперболический синус
tanh(x) - гиперболический тангенс
floor(x) - округление с недостатком
ceil(x) - округление с избытком
sign(x) - знак числа
inv(x) - логическая инверсия
- - отрицание
Бинарные операции:
(по приоритету с наименьшего)
x+y = add (x, y) - сложение x с y
x-y = sub (x, y) - вычитание из x y
x*y = mul (x, y) - умножение x на y
x/y = div (x, y) - деление x на y
x&y = log (x, y) - логарифм от x по основанию y
x^y = pow (x, y) - возведение x в степень y
x=y = x==y = equal (x, y) - если x = y, то 1 иначе 0
x<y = less (x, y) - если x < y, то 1 иначе 0
x>y = greater (x, y) - если x > y, то 1 иначе 0
and (x, y) - логическое И
or (x, y) - логическое ИЛИ
xor (x, y) - логическое сложение по модулю 2 (операция, исключающая ИЛИ) - сумма Жегалкина
pirs (x, y) - стрелка Пирса
shef (x, y) - штих Шеффера
impl (x, y) - логическая импликация
eq (x, y) - логическая эквиваленция
less (x, y) - x<y?
greater (x, y) - x>y?
less_or_equal (x, y) - x<=y?
greater_or_equal (x, y) - x>=y?
max (x, y) - большее из x и y
min (x, y) - меньшее из x и y
equal (x, y) - эквиваленция
percent (x, y) - процент y от x
rand (x, y) - случайное число от x до y
Для всех логических операций число отличное от 0 это 1 (ПРАВДА), иначе 0 (ЛОЖЬ).
Числа пишутся в диапазоне [-1.7976931348623158e+308, 1.7976931348623158e+308]. Числа всегда записываются в десятичной форме, например 1 1f 1.0 1,0 1.0f 1,0f - одно и то же число в шести разных формах. Нельзя записывать числа в экспонентной форме, например 2.3e-5, вместо этого 2.3*(10^-5). Можно использовать константы: pi – число π, e – число e. Переменной является буква x. Между функциями можно ставить разделитель – пробел(space).
Чтобы сохранить изображение выберите во вкладке Файл -> Сохранить или Сохранить как. При этом появится стандартное диалоговое окно сохранения, где выбирается путь для сохранения. Изображения сохраняются в формате png.
6. Ограничения данной версии программы
Гарантируется работа данной программы в операционной системе Windows не ниже 98. В предыдущих версиях работа программы не проверялась.
При работе с программой нужно пользоваться правилами, которые приведены в разделе Описание работы программного продукта. В этом случае гарантируется правильная работа программы. Причем нужно обязательно соблюдать правила ввода функции, интерпретатор в этом случае поймет функцию правильно. Если в поле ввода функции ввести что-то неоговоренное правилами, интерпретатор примет это значение в любом случае, и не будет выведено никакого сообщения. Интерпретатор поймет, то что сможет распознать, остальное он игнорирует. Например, если будет введено “zxczxc” или пустая строка, то функция воспримется, как f(x)=0. Если будет введено “dghld+sin(x)asdfasf+dfgdfg”, то функция воспримется, как f(x)=sin(x).
7. Вывод
Написанная мною программа, позволяет решать важнейшую задачу математического анализа – построение графиков функций. Она может облегчить работу исследования функций. Программный продукт GRAPHIC может быть использован для учебных целей.
Программа написана при использовании самых современных на сегодняшний день технологий программирования и обеспечивает быструю и качественную работу.
Список используемой литературы
1. Язык программирования Си++. Курс лекций. Учебное пособие / Издание второе, исправленное / Фридман А. Л. / М.: «Интернет-университет Информационных Технологий», 2004.– 264 с.
2. Язык Си++. Учебное пособие / Издание пятое / Подбельский В. В. / М.: Финансы и статистика, 2001.– 560 с.: ил.
3. http: //www.holzner.ru.
4. http: //www.firstsleps.ru.
5. http: //www.intuit.ru.
Похожие работы
... работа как прием обучения может входить почти во все методы обучения, воспитывать в учениках потребность самостоятельно добывать знания, умение творчески пользоваться объяснениями учителя, помощью товарищей, книгами, конспектами одна из важнейших целей нашей работы.ГЛАВА 2. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИЙ ПРИЁМЫ И МЕТОДЫ §1. Анализ программ и учебников «Алгебра, 7», «Алгебра, ...
... быть перечислены через запятую). Всякое уравнение с одним неизвестным может быть записано в виде, f(x)=0, где f(x) – нелинейная функция. Решение таких уравнений заключается в нахождении корней, т.е. тех значений неизвестного x, которые обращают уравнение в тождество. Точное решение нелинейного уравнения далеко не всегда возможно. На практике часто нет необходимости в точном решении уравнения. ...
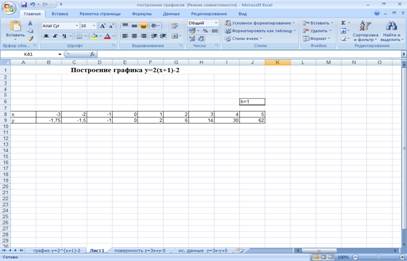
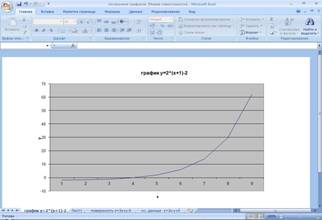
... может быть оформлена или переделана — может быть изменен ее тип, заданы названия осей, способ отображения легенды, цвета, подписи и другие параметры. 2 глава. Построение графика и поверхности 2.1 Ход построения графика y=2(x+1)-2 Построение графиков: Объедините ячейки А1-I1. В созданную ячейку введите заголовок Построение графика функции y=2(x+1)-2 в А8 − Х, в А9 − У, в В2 ...
... (вопросы а) и в)). Понятие функции, в системе формирования которого должны присутствовать такие задания, сразу выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения. Методика введения понятий: функции, аргумента, области определения. Не смотря на чрезвычайно большой объем, широту и сложность понятия функции, его ...





0 комментариев