Проранжируем y Є Y(k) в порядке убывания величин Ну

1.  Проранжируем y Є Y(k) в порядке убывания величин Ну.

2.  Выберем yk такой, что НУк = min НУi. Удалим yk из множества У (k). Обозначим Уост (k) = Y (k)\yk.

3.Осуществим привязку абонентов ХУк к оставшимся ВЦ по критерию минимума затрат на связь. Новое значение критерия

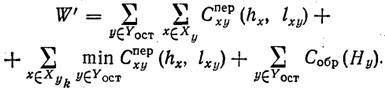
4.Сравним величины W‘ и Wk. Возможны два случая: 1) W‘≤Wk; 2) W‘>Wk.

В 1-м случае принимаем Y(k+1) = Yост(k), и итерация заканчивается. Во 2-м случае выбираем следующий по порядку пункт ук-1 и переходим к шагу 3.

Шаги 3 и 4 повторяются многократно до тех пор, пока либо очередной шаг 4 не закончится 1-м случаем, что означает конец итерации, либо множество Y(k) будет просмотрено полностью и ни один вариант укрупнения не приведет к улучшению величины критерия. Это является признаком окончания работы алгоритма.

2.2 Оптимизация структуры абонентских СДО в классе древовидных сетей

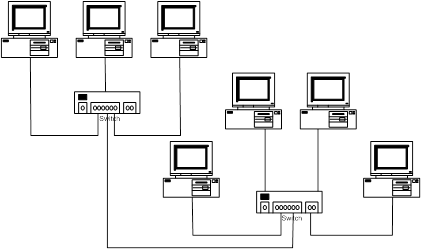
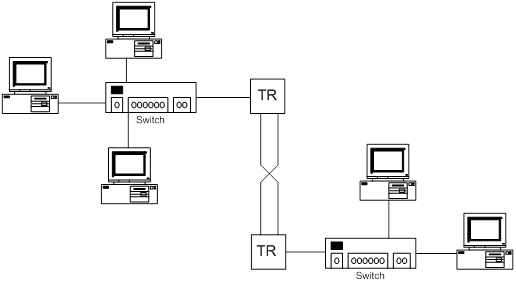
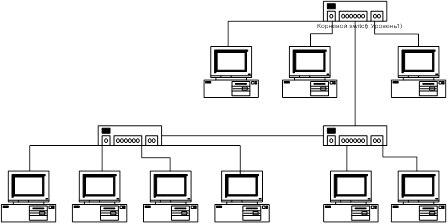
Распространенный класс абонентских СДО для централизованных сетей ЭВМ составляют так называемые древовидные, структура которых представляет собой дерево или совокупность деревьев с корнями, которые соответствуют местам размещения РЦ. Такая структура получается, когда абонентские пункты (АП) подключают друг к другу по так называемой многопунктовой схеме. Применение многопунктовых сетей позволяет сократить капитальные затраты на создание СДО, повысить коэффициент использования каналов передачи данных, сократить общую протяженность сетей по сравнению с СДО радиальной структуры, в которой используются выделенные каналы для всех АП.

Задача синтеза абонентской СДО в классе древовидных сетей формулируется следующим образом. Заданы множество абонентов X = {xj}, характеризуемых своими географическими координатами местонахождения {δj, wj} и объемами информации hj, а также места размещения РЦ и привязки абонентов к РЦ Хyi., i = 1, т. Известны приведенные затраты на передачу информации от пункта i к пункту j: . Требуется синтезировать структуру абонентской СДО в классе древовидных структур минимальной стоимости при ограничениях на суммарный поток (трафик) fij в каждой ветви (i, j): fij ≤ dmax, где dmax— пропускная способность многопунктовой сети; fij определяется как сумма информационных потоков от всех узлов, предшествующих узлу i на путях от концевых вершин к корню дерева, и потока hi, определяемого абонентом xi.

Рассмотрим некоторые наиболее важные работы и алгоритмы решения этой задачи.

2.2.1 Алгоритм Прима

Задача синтеза древовидной сети впервые рассмотрена в работе Прима, в которой предложен точный алгоритм синтеза сети минимальной стоимости.

Первоначально рассмотрим исходное множество несвязанных узлов (вершин) X = {xi}.

1.  Выбираем произвольный узел (подграф) xi и отыскиваем стоимость ввода ребра (i, j), связывающего xi с некоторым подграфом xjcij. Если подграфы хi и xj состоят из нескольких узлов, то отыскиваем ребро, связывающее ближайшую пару узлов xj и xil , принадлежащих к разным подграфам.

2.  Среди всех пар (i, j) находим такую (i*, j*), что сi*j* = min cij.

3.  Объединяем подграфы  и  в один:  = .

На этом одна итерация метода заканчивается. Таким образом, на каждой итерации число изолированных подграфов сокращается. Как только их число N станет равно 1, работа алгоритма заканчивается. Доказано, что данный алгоритм позволяет получить оптимальное решение. Заметим, что в задаче Прима не вводятся ограничения на пропускные способности сети, и поэтому отсутствует ограничение на суммарный поток frl, передаваемый по произвольной ветви (r, l). Таким образом, алгоритм Прима позволяет синтезировать кратчайшее связывающее дерево (КСД) без ограничений. Практически гораздо более важной является задача синтеза КСД с ограничениями на суммарный поток frl, определяемый пропускными способностями КС drl.

2.2.2 Алгоритм Исау-Вильямса

Одним из наиболее известных и распространенных алгоритмов синтеза КСД с ограничениями является алгоритм Исау—Вильямса, известный под названием CNDP. Предположим, что рц обработки данных расположен в пункте х1, а пропускная способность всех ветвей одинакова и равны d.

Пусть первоначально имеется некоторое множество изолированных узлов X — {x1,… хn}. Для каждого узла i вычисляем стоимость его подключения к РЦ сi1 = vi, а также стоимость связи сij двух узлов i и j между собой. В общем случае cij = cij(hi), где hi — поток информации в узле i. Вычисляем экономию от подключения узла i к j вместо подключения его к РЦ: Eij = cij — ci1 = cij — vi. Находим такую пару (i*, j*), для которой Ei*j* = min Еij при условии, что hi*-hj*≤d. Если Ei*j* < 0, то вводим ветвь (i*, j*) и объединяем два узла xi* и xj* в один: Xi*H = xi*⋃xj*, при этом определяем новое значение потока информации Нi* = hi*. Пусть проведено k итераций и построено k обобщенных узлов (подграфов) X1 Х2, ... , Хк и пусть Hk = H(Xk) — суммарный информационный поток всех узлов, входящих в Xk.

Опишем (k+1)-ю итерацию. Выбираем произвольный изолированный подграф Xi. Находим произвольный подграф Xj и проверяем возможность ввода ребра (i, j): Hi + Hj ≤. d.

Если условие выполняется, то вычисляем Eij = cij(Hi) - vi.

Находим такую пару (i*, j*), для которой Ei*j* =; min Еij.

Если Ei*j* < 0, то объединяем пару подграфов Xi и Xj в один: Xi* = Xj* = Xi* ⋃ Xj*, в противном случае подключаем все оставшиеся изолированные подграфы напрямую к РЦ, и конец работы алгоритма.

Алгоритм Краскала отдельно рассматривать не стоит, так как он аналогичен уже описанному. Отличительной особенность является то, что в начале все узлы изолированы, на каждом шаге отыскивают наименьшую по стоимости допустимую линию связи различных узлов.

2.2.3 Алгоритм Шарма

Определяют полярные координаты (аi, ri) каждого терминала относительно РЦ. Терминалы (узлы) рассматривают в последовательности, соответствующей возрастанию угла полярных координат ai, так что а1 ≤ а2 ≤ ...≤ ап. Строят минимальную по стоимости древовидную сеть терминалов х1, х2,…хк и РЦ, где х1, х2,…хк удовлетворяют ограничениям, но при добавлении хк+1 к многопунктовой (многоточечной) сети ограничения нарушаются. Вышеуказанную процедуру, начиная с хк+1 повторяют до тех пор, пока все терминалы не будут включены в дерево.

Как следует из описания, все перечисленные алгоритмы близки друг к другу и различаются только очередностью объединения компонент, которая обеспечивается назначением соответствующих весов значимости этим компонентам (узлам).

2.2.4 Алгоритм Фогеля (VАМ)

Для каждого терминала (узла) хi подсчитывают выигрыш Ei как разность Еi = с’ij — сij, где Xj — ближайший к хi подграф; X’j — следующий по порядку ближайший к хi подграф.

Текущая итерация алгоритма заключается в том, что находится i* такой, что Ei*= max Еi. Проводится проверка по ограничению: если оно выполняется, то хi подключается к ближайшему узлу хj. В результате образуется некоторый подграф Хi = xi ⋃ xj. Стоимость связи между двумя сегментами определяется как стоимость самой дешевой связи между двумя терминалами (узлами), принадлежащими разным подграфам. Если связь (i, j) нарушает ограничение по ПС, то сij = ∞. Когда все терминалы оказываются подключенными к РЦ, конец работы алгоритма.

2.2.5 Унифицированный алгоритм синтеза КСД

В результате анализа известных алгоритмов синтеза КСД (алгоритмы Прима, Исау — Вильямса, Краскала, Шарма и т. д.) предложен так называемый унифицированный алгоритм синтеза многопунктовых сетей, из которого можно получить как частный случай любой из известных алгоритмов синтеза, приписав определенные значения некоторым формальным параметрам. Для формального описания алгоритма введем следующие обозначения: vi — вес терминала i; Хi — подграф (набор терминалов), содержащий терминал i; (i, j) — линия, соединяющая терминалы i и j; Еij — экономия, соответствующая линии (i, j); cij — стоимость связи (i, j); N — число терминалов.

Шаг 0. 1. Задаем начальные значения величины vi для i = 1,2…N, используя соответствующее правило из таблицы 2.1.

2.Устанавливаем Хi = {i}, i = 1,2…N.

3.Определяем Еij =cij-vi для (i, j), если сij существует и терминалы (узлы) i и j не объединены.

Таблица 2.1 – Инициализация и коррекция весов

Алгоритм	Инициализация весов	Коррекция весов при вводе связи (i, j)
Прима	vi = 0, i = 1 vi = - ∞, i = 2,…,N	0 -> vj, vi = 0
Исау-Вильямса	vi = ci1, i = 2,N	vi = vj
Краскала	vi = 0, i = 1,N	Нет
Фогеля	v*i = bi - ai	v**i = bi - ai

* Для определения bi, аi см. описание алгоритма.

** Величины bi, аi определяются с учетом вновь введенных компонент.

Шаг 1. Определяем Еi*j* = min Еij. Если Еi*j* = ∞, то заканчиваем поиск, в противном случае переходим к шагу 2.

Шаг 2. Оцениваем выполнение ограничений для Хi* ⋃ Xj* (объединения подграфов). Если любое из них нарушено (например, ограничение, что Нi + Hj < d), то устанавливаем Еi*j* = ∞ и возвращаемся к шагу 1. В противном случае переходим к шагу 3.

Шаг 3. 1. Вводим ветвь (i, j).

2.Изменяем величины vi для i = 1,2…N (таблица 1 и примечание 4).

3.Еij =cij-vi для тех i, для которых vi изменено.

4.Сформируем новый подграф Хi* ⋃ Xj*. Повторно пересчитываем ограничения и возвращаемся к шагу 1.

Примечания:

1.Для простоты изложения принимаем, что центр обработки данных находится в пункте 1.

2.  Правила оценки весов vi используют для назначения терминалам весов значимости. Они приписывают им числовые значения, соответствующие степени желаемого использования линий, исходящих из каждого терминала.

3.  Величина Еij может быть определена только в том случае, если имеется ветвь (ij) и компоненты, содержащие терминалы i и j, можно соединить без нарушения каких бы то ни было ограничений. В противном случае значение Еij является неопределенным и для удобства расчетов полагаем Еij = ∞.