Навигация
Решим исходную задачу симплексным методом
2. Решим исходную задачу симплексным методом.
Запишем ее канонический вид:
![]()
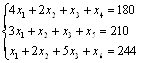
![]() ,
, ![]() .
.
![]() х4, х5, х6 – дополнительные и они же базисные переменные. Начальный опорный план
х4, х5, х6 – дополнительные и они же базисные переменные. Начальный опорный план ![]() (0; 0; 0; 180; 210; 244).
(0; 0; 0; 180; 210; 244).
| Базис |
| В | 10 | 14 | 12 | 0 | 0 | 0 |
|
|
|
|
|
|
|
| ||||
|
| 0 | 180 | 4 | 2 | 1 | 1 | 0 | 0 | 90 |
|
| 0 | 210 | 3 | 1 | 1 | 0 | 1 | 0 | 210 |
|
| 0 | 244 | 1 | 2 | 5 | 0 | 0 | 1 | 122 |
|
| 0 | –10 | –14 | –12 | 0 | 0 | 0 | таб. 1 | |
| Базис |
| В | 10 | 14 | 12 | 0 | 0 | 0 |
|
|
|
|
|
|
|
| ||||
|
| 14 | 90 | 2 | 1 | 0,5 | 0,5 | 0 | 0 | 180 |
|
| 0 | 120 | 1 | 0 | 0,5 | –0,5 | 1 | 0 | 240 |
|
| 0 | 64 | –3 | 0 | 4 | –1 | 0 | 1 | 16 |
|
| 1260 | 18 | 0 | –5 | 7 | 0 | 0 | таб. 2 | |
|
| 14 | 82 | 2,375 | 1 | 0 | 0,625 | 0 | –0,125 | |
|
| 0 | 80 | 1,375 | 0 | 0 | 0,125 | 1 | –0,625 | |
|
| 12 | 16 | –0,75 | 0 | 1 | –0,25 | 0 | 0,25 | |
|
| 1340 | 14,25 | 0 | 0 | 5,75 | 0 | 1,25 | таб. 3 | |
|
|
|
|
|
|
| ||||
Так как все оценки ![]() , то получен оптимальный план:
, то получен оптимальный план:
![]() = (0; 82; 16; 0; 80; 0);
= (0; 82; 16; 0; 80; 0); ![]() = 1340.
= 1340.
3. Найдем оптимальное решение двойственной задачи, используя последнюю проверочную строку симплексной таблицы и соотношение между переменными прямой и двойственной задач.
|
| дополнительные переменные | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| дополнительные переменные | основные переменные | ||||
Откуда: ![]() 5,75;
5,75; ![]() 0;
0; ![]() 1,25;
1,25; ![]() 14,25;
14,25; ![]() 0;
0; ![]() 0.
0.
![]() = (5,75; 0; 1,25; 14,25; 0; 0);
= (5,75; 0; 1,25; 14,25; 0; 0); ![]() 1340.
1340.
Таким образом получили ![]() =
=![]() 1340.
1340.
4. Проанализируем основные и дополнительные переменные оптимальных решений обеих задач. Основные переменные исходной задачи – это планируемый выпуск продукции.
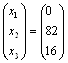
Продукцию І-го вида к выпуску не планируют, ІІ-го вида – в количестве 82 ед. и ІІІ-го вида – в количестве 16 ед.
Дополнительные переменные исходной задачи показывают остатки сырья.
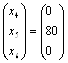
Сырье І и ІІІ видов израсходовано полностью. А сырье ІІ вида осталось в количестве 80 ед.
Основные переменные двойственной задачи характеризуют дефицитность сырья: если ![]() , то сырье дефицитное; если
, то сырье дефицитное; если ![]() , то сырье недефицитное.
, то сырье недефицитное.

Таким образом, сырье І и ІІІ видов дефицитное, причем наиболее дефицитное сырье І-го вида. Сырье ІІ вида недефицитное.
Дополнительные переменные двойственной задачи характеризуют рентабельность продукции. При этом, если ![]() , то продукция нерентабельна.
, то продукция нерентабельна.

По этому соотношению видно, что продукция І вида нерентабельна, а ІІ и ІІІ – рентабельна.
Ответ: ![]() = (0; 82; 16; 0; 80; 0);
= (0; 82; 16; 0; 80; 0); ![]() = 1340;
= 1340;
![]() = (5,75; 0; 1,25; 14,25; 0; 0);
= (5,75; 0; 1,25; 14,25; 0; 0); ![]() 1340
1340
Наиболее дефицитное сырье І вида. Наиболее убыточный І вид продукции.
Задания для самостоятельной работы.
Для производства четырех видов продукции (П1, П2, П3, П4) используются три вида ресурсов. Норма затрат ресурсов, использованных для выпуска единицы продукции каждого вида, цена единицы продукции и запасы ресурсов приведены в таблице.
Построить модель прямой и двойственной задач. Найти оптимальный план для обеих задач и экстремальные значения целевых функций. Дать экономическую интерпретацию основным и дополнительным переменным исходной и двойственной задач.
| Ресурсы Продукция | Затраты ресурсов на единицу продукции | Объем ресурсов | |||
| П1 | П2 | П3 | П4 | ||
| Р1 | 2 | 3 | 4 | 4 | 2100 |
| Р2 | 5 | 5 | 0 | 7 | 2800 |
| Р3 | 8 | 7 | 10 | 9 | 3000 |
| Цена единицы | 60 | 65 | 55 | 62 | |
Транспортная задача возникает при планировании рациональных перевозок грузов. Математическая модель транспортной задачи в простейшем случае имеет вид:
![]() max (1)
max (1)
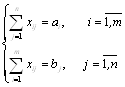 (2)
(2)
![]() ,
, ![]() ,
, ![]() (3)
(3)
Здесь: ![]() – запасы поставщиков;
– запасы поставщиков;
![]() – спрос потребителей;
– спрос потребителей;
![]() – тарифы, т.е. стоимости перевозки единицы груза от
– тарифы, т.е. стоимости перевозки единицы груза от ![]() -го поставщика к
-го поставщика к ![]() -му потребителю;
-му потребителю;
Z – транспортные расходы;
![]() - количество продукта, перевозимого от
- количество продукта, перевозимого от ![]() -го поставщика к
-го поставщика к ![]() -му потребителю.
-му потребителю.
Обычно транспортную задачу задают тремя матрицами: матрицей поставщиков, матрицей потребителей и матрицей тарифов.
Для наглядности транспортную задачу представляют в виде распределительной таблицы.
Любая транспортная задача имеет допустимое решение (матрицу перевозок ![]() ), если
), если
![]() (4)
(4)
Если условие (4) выполняется, то транспортную задачу называют транспортной задачей закрытого типа.
Допустимое решение транспортной задачи часто называют планом перевозок.
1) Построение начального опорного плана. Его вырожденность или невырожденность. Ранг матрицы системы. а) Метод северо-западного угла.Заполнение распределительной таблицы начинают с клетки (1; 1), при этом ![]() . Далее смещаются или по строке вправо или по столбцу вниз до клетки
. Далее смещаются или по строке вправо или по столбцу вниз до клетки ![]() . Заполненные клетки должны распространяться так, чтобы их можно было соединить ломаной линией, звенья которой взаимно перпендикулярны.
. Заполненные клетки должны распространяться так, чтобы их можно было соединить ломаной линией, звенья которой взаимно перпендикулярны.
Пример. Построить методом северо-западного угла начальный опорный план для транспортной задачи: поставщики а = (20; 30; 40); потребители ![]() = (15; 35; 20; 20); тарифы перевозок
= (15; 35; 20; 20); тарифы перевозок
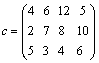
Найти стоимость перевозок.
Решение. Строим распределительную таблицу и находим груз х11 = min (20; 15) = 15. По первому столбцу не перемещаемся, так как спрос І потребителя удовлетворен. Перемещаемся по І строке в клетку (1; 2):
х12 = min (а1 – х11; b2) = min (5; 35) = 5.
Теперь переходим по ІІ столбцу в клетку (2; 2):
х22 = min (30; b2 – х12) = min (30; 30) = 30.
Так как спрос ІІ потребителя удовлетворен и у ІІ поставщика продукция уже выбрана, то переходим к клетке (3; 3):
х33 = min (40; 20) = 20.
х34 = min (а3 – х33; b4) = min (20; 20) = 20.
Таким образом, получен план перевозок:
|
| 15 | 35 | 20 | 20 | ||||
| 20 | 4 | 6 | 12 | 5 | ||||
| 15 | 5 | |||||||
| 30 | 2 | 7 | 8 | 10 | ||||
| 30 | ||||||||
| 40 | 5 | 3 | 4 | 6 | ||||
| 20 | 20 | |||||||
Для подсчета стоимости перевозок нужно количество груза в каждой заполненной клетке умножить на соответствующий тариф в этой клетке и результаты сложить.
![]() .
.
Строим распределительную таблицу и начинаем ее заполнять с той клетки, в которой наименьший тариф.
Пример. Построить начальный опорный план методом минимальной стоимости и найти транспортные расходы для транспортной задачи: поставщики а = (20; 30; 40); потребители ![]() = (15; 35; 20; 20); тарифы перевозок
= (15; 35; 20; 20); тарифы перевозок
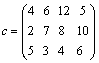
Решение. Строим распределительную таблицу и начинаем ее заполнять с клетки (2; 1), т. к. в ней наименьший тариф х21 = min (30; 15) = 15.
|
| 15 | 35 | 20 | 20 | ||||
| 20 | 4 | 6 | 12 | 5 | ||||
| 20 | ||||||||
| 30 | 2 | 7 | 8 | 10 | ||||
| 15 | 15 | |||||||
| 40 | 5 | 3 | 4 | 6 | ||||
| 35 | 5 | |||||||
Потом заполняем клетку (3; 2) с тарифом с32 = 3;
х32 = min (40; 35) = 35.
Далее х33 = min (а3 – х32; b3) = (5; 20) = 5;
х14 = min (20; 20) = 20;
х23 = min (а2 – х21; b3 – х33) = min (15; 15) = 15.
![]() .
.
Сравнивая значение Z в а) и б), видим, что учитывая стоимости перевозок, затраты при втором методе значительно меньше.
Рангом матрицы системы (2) называют число ![]() , т.е. количество строк плюс количество столбцов и минус единица. Если число заполненных клеток в распределительной таблице равно рангу матрицы, то полученный план называется не вырожденным. В противоположном случае – вырожденным.
, т.е. количество строк плюс количество столбцов и минус единица. Если число заполненных клеток в распределительной таблице равно рангу матрицы, то полученный план называется не вырожденным. В противоположном случае – вырожденным.
В пунктах а) и б) ![]() , а число заполненных клеток 5. Следовательно, полученные планы – вырожденные.
, а число заполненных клеток 5. Следовательно, полученные планы – вырожденные.
Допустимое решение транспортной задачи является оптимальным тогда и только тогда, когда можно найти такие числа – потенциалы ![]() ,
, ![]() и
и ![]() ,
, ![]() , которые удовлетворяют следующим условиям:
, которые удовлетворяют следующим условиям:
I.
II. ![]() для всех заполненных клеток; (5)
для всех заполненных клеток; (5)
III. ![]() для всех пустых клеток. (6)
для всех пустых клеток. (6)
На основании первого условия оптимальности потенциалы находят из условий ![]() и один, произвольно выбранный, потенциал приравнивают к нулю, например
и один, произвольно выбранный, потенциал приравнивают к нулю, например ![]() .
.
Если при проверке второго условия оптимальности окажется, что ![]() для всех незаполненных клеток, то опорный план оптимален и соответствующее значение целевой функции Z определяет минимальные расходы. Если же найдется хотя бы одна клетка, для которой
для всех незаполненных клеток, то опорный план оптимален и соответствующее значение целевой функции Z определяет минимальные расходы. Если же найдется хотя бы одна клетка, для которой ![]() , то план не оптимальный и можно перейти к нехудшему опорному плану.
, то план не оптимальный и можно перейти к нехудшему опорному плану.
Переход к не худшему опорному плану осуществляют при помощи цикла перераспределения груза. Цикл представляет собой замкнутую ломаную, звенья которой взаимно перпендикулярны и вершины цикла, кроме одной, находятся в заполненных клетках.
Приведем примеры разновидностей форм циклов:
В каждом случае только одна вершина цикла находится в незаполненной клетке. Ее называют началом цикла и определяют по наибольшему нарушению условия оптимальности (6), т.е. по максимальной оценке ![]() . Клетке начала цикла присваивают знак «+», во всех остальных вершинах цикла знаки чередуют «–», «+» и т.д. Из клеток цикла со знаками «–» выбирают ту, в которой находится минимальный груз. Это и будет то количество груза, которое нужно перераспределить по циклу, т.е. в клетке со знаком «+» это количество груза прибавляется, а со знаком «–» – вычитается. Клетки, которые не задействованы в цикле, остаются неизменными.
. Клетке начала цикла присваивают знак «+», во всех остальных вершинах цикла знаки чередуют «–», «+» и т.д. Из клеток цикла со знаками «–» выбирают ту, в которой находится минимальный груз. Это и будет то количество груза, которое нужно перераспределить по циклу, т.е. в клетке со знаком «+» это количество груза прибавляется, а со знаком «–» – вычитается. Клетки, которые не задействованы в цикле, остаются неизменными.
Таким образом, получаем новый опорный план. Подсчитываем транспортные расходы, которые должны быть не более предыдущих. В противном случае где-то допущена ошибка. Новый план опять проверяем на оптимальность, используя условия (5) и (6). Если план оптимальный, то задача решена. Если же план опять не оптимальный, то работаем, согласно пункту 3) до получения оптимального плана и нахождения Zmin.
Транспортная задача открытого типаЕсли для транспортной задачи выполняется одно из условий
![]() или
или
![]() ,
,
то модель задачи называют открытой. Чтобы такая задача имела решение, необходимо ее привести к закрытому типу, т.е. чтобы выполнялось равенство ![]() .
.
Это делают так: если ![]() , то добавляют фиктивного потребителя со спросом
, то добавляют фиктивного потребителя со спросом ![]() (в распределительной таблице появится дополнительный столбец), если
(в распределительной таблице появится дополнительный столбец), если ![]() , то добавляют фиктивного поставщика с предложением
, то добавляют фиктивного поставщика с предложением ![]() (в распределительной таблице появится дополнительная строка). В обоих случаях тарифы полагают равными нулю. Далее задача решается по такому же порядку, как было рассмотрено ранее.
(в распределительной таблице появится дополнительная строка). В обоих случаях тарифы полагают равными нулю. Далее задача решается по такому же порядку, как было рассмотрено ранее.
Запишем алгоритм решения транспортной задачи:
1) Проверка типа модели ТЗ.
2) Построение начального опорного плана (любым способом).
3) Проверка плана на вырожденность.
4) Проверка плана на оптимальность методом потенциалов:
а) нахождение потенциалов из системы
![]() (для всех заполненных клеток);
(для всех заполненных клеток);
б) проверка второго условия оптимальности
![]() (для всех пустых клеток).
(для всех пустых клеток).
5) Переход к нехудшему опорному плану (если это необходимо).
Пример. На складах имеются запасы однотипного товара в количестве а (35; 40; 40; 50), который необходимо доставить потребителям. Потребности потребителей задает вектор b (31; 52; 17; 20). Матрица затрат на доставку единицы товара от i-го поставщика j-му потребителю:
с=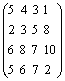
Составить план перевозок с минимальными транспортными затратами.
Решение. Определим тип модели транспортной задачи. Суммарная мощность поставщиков: ![]() 35+40+40+50=165 (единиц товара); Суммарный спрос потребителей:
35+40+40+50=165 (единиц товара); Суммарный спрос потребителей: ![]() 31+52+17+20=120 (единиц товара).
31+52+17+20=120 (единиц товара).
Т.к. ![]()
![]() , то имеем модель открытого типа.
, то имеем модель открытого типа.
Введем фиктивного потребителя, спрос которого равен
![]()
![]()
![]() 165 –120 =45 (единиц товара).
165 –120 =45 (единиц товара).
Тарифы ![]() 0. Т.о. получаем модель закрытого типа, m = 4 – число поставщиков, n = 5 – число потребителей. Ранг матрицы задачи
0. Т.о. получаем модель закрытого типа, m = 4 – число поставщиков, n = 5 – число потребителей. Ранг матрицы задачи ![]() . Построим начальный опорный план методом минимального элемента (наименьшей стоимости).
. Построим начальный опорный план методом минимального элемента (наименьшей стоимости).
|
| 31 | 52 | 17 | 20 | 45 |
| |||||
| 35 | 5 | 4 | 3 | 1 | 0 | 0 | |||||
| 15 | 20 | ||||||||||
| 40 | 2 | 3 | 5 | 8 | 0 | 1 | |||||
| 31 | 9 | ||||||||||
| 40 | 6 | 8 | 7 | 10 | 0 | 4 | |||||
| 40 | |||||||||||
| 50 | 5 | 6 | 7 | 2 | 0 | 4 | |||||
| 43 | 2 | 5 | |||||||||
|
| 1 | 2 | 3 | 1 | – 4 | Таб.1 | |||||
Число заполненных клеток распределительной таблицы 8 равно рангу матрицы задачи r = 8, следовательно, опорный план является невырожденным.
Транспортные затраты, соответствующие опорному плану:
![]() (ден. ед.).
(ден. ед.).
Исследуем опорный план на оптимальность, используя метод потенциалов.
Дополним таблицу 1 столбцом и строкой потенциалов ![]() и
и ![]() . Систему потенциалов найдем, используя первое условие оптимальности: для заполненных поставками клеток
. Систему потенциалов найдем, используя первое условие оптимальности: для заполненных поставками клеток ![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Из записанной системы находим: ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Проверим выполнение второго условия оптимальности. Для всех пустых клеток должно выполняться неравенство: ![]() .
.
(1; 1) ![]() 0 + 1 – 5 = –4
0 + 1 – 5 = –4![]() 0;
0;
(1; 2) ![]() 0 + 2 – 4 = –2
0 + 2 – 4 = –2![]() 0;
0;
(1; 5) ![]() 0 – 4 – 0 = –4
0 – 4 – 0 = –4![]() 0;
0;
(2; 3) ![]() 1 + 3 – 5 = –1
1 + 3 – 5 = –1![]() 0;
0;
(2; 4) ![]() 1 + 1 – 8 = –6
1 + 1 – 8 = –6![]() 0;
0;
(2; 5) ![]() 1 – 4 – 0 = –4
1 – 4 – 0 = –4![]() 0;
0;
(3; 1) ![]() 4 + 1 – 6 = –1
4 + 1 – 6 = –1![]() 0;
0;
(3; 2) ![]() 4 + 2 – 8 = –2
4 + 2 – 8 = –2![]() 0;
0;
(3; 3) ![]() 4 + 3 – 7 = 0
4 + 3 – 7 = 0![]() 0;
0;
(3; 4) ![]() 4 + 1 – 10 = –5
4 + 1 – 10 = –5![]() 0;
0;
(4; 1) ![]() 4 + 1 – 5 = 0
4 + 1 – 5 = 0![]() 0;
0;
(4; 4) ![]() 4 + 1 – 2 = 3
4 + 1 – 2 = 3![]() 0.
0.
Т.к. среди свободных клеток есть такие, в которых второе условие оптимальности не выполняется, то план не оптимален.
Осуществим переход к нехудшему опорному плану. Наиболее перспективная для заполнения клетка (4; 4), т. к. ей соответствует наибольшая положительная оценка
![]() 4 + 1 – 2 = 3.
4 + 1 – 2 = 3.
Найдем цикл перераспределения груза для этой клетки.
Выбранной для заполнения клетке присваиваем знак «+», далее знаки чередуем. Среди вершин со знаком «–» выбираем наименьшую поставку.
![]() – объем перепоставки.
– объем перепоставки.
Перераспределим поставки по циклу, тем самым перейдем к новому опорному плану.
|
| 31 | 52 | 17 | 20 | 45 |
| |||||
| 35 | 5 | 4 | 3 | 1 | 0 | 0 | |||||
| 17 | 18 | ||||||||||
| 40 | 2 | 3 | 5 | 8 | 0 | –2 | |||||
| 31 | 9 | ||||||||||
| 40 | 6 | 8 | 7 | 10 | 0 | 1 | |||||
| 40 | |||||||||||
| 50 | 5 | 6 | 7 | 2 | 0 | 1 | |||||
| 43 | 2 | 5 | |||||||||
|
| 4 | 5 | 3 | 1 | –1 | Таб.2 | |||||
 Транспортные затраты, соответствующие опорному плану:
Транспортные затраты, соответствующие опорному плану:
![]() (ден. ед.).
(ден. ед.).
Исследуем опорный план на оптимальность. Найдем значения потенциалов, используя первое условие оптимальности. Для заполненных поставками клеток ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Проверим выполнение второго условия оптимальности. Для всех пустых клеток должно выполняться неравенство: ![]() .
.
Выпишем клетки, в которых условие нарушено:
(1; 2) ![]() 0 + 5 – 4 = 1
0 + 5 – 4 = 1![]() 0.
0.
Осуществим переход к нехудшему опорному плану. Наиболее перспективная для заполнения клетка (1; 2), т. к. ей соответствует положительная оценка
Похожие работы
... . Они могут также базироваться на «здравом смысле», то есть на логических суждениях, последовательных доказательствах, опирающихся на практический опыт. В основе эвристических методов обоснования управленческих решений лежат субъективные суждения менеджеров. Достоинство эвристических методов – оперативность принятия; недостаток – отсутствие гарантии в надежности интуиции. В состав данной группы ...
... посредством организации конкурсов бизнес-идей, мини-олимпиад, работы творческих групп и пр. С целью их проведения в исследовании разработан сборник экономических задач, основанный на предложенном подходе к интеграции математического и экономического содержания, рассмотрена технология организации такого типа мероприятий. Трудности применения математических методов в экономике Трудности ...
... -педагогическая или научно-техническая проблема, являющаяся новым научным вкладом в теорию определенной области знаний (педагогику, технику и другие). 4. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ВЫПОЛНЕНИЯ ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ БАКАЛАВРА ФИЗИКО-МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ ПРОФИЛЬ ИНФОРМАТИКА 4.1. Положение о выпускной квалификационной работе бакалавра физико-математического образования: ...
... работы со справочной системой работа практикума приостанавливается. 3. Организационно-экономическое обоснование проекта В ходе дипломного проекта был разработан компьютерный лабораторный практикум по курсу «Теория оптимизации и численные методы». В данном разделе рассмотрена экономическая сторона проекта. Рассмотрены следующие вопросы: 1) сетевая модель 2) расчёт ...
 основныепеременные
основныепеременные
0 комментариев