ЗАДАЧИ СТАТИКИ, РЕШАЕМЫЕ С ПОМОЩЬЮ ЯЗЫКА ПАСКАЛЬ

2.1. ЗАДАЧИ СТАТИКИ, РЕШАЕМЫЕ С ПОМОЩЬЮ ЯЗЫКА ПАСКАЛЬ

Основной задачей статики является изучение методов замены различных систем сил, действующих на абсолютно твердое тело, простейшими системами, оказывающими на тело такое же действие, как и исходная система.

Выяснение условий взаимной уравновешенности системы сил является одной из основных задач статики.

На основе изложенной в первой главе курсовой работы алгоритм конструкции языка программирования Паскаль составим и решим ряд задач по прикладной механике.

Сформулируем задачу по статике первому разделу прикладной механики.

Задача. Найти центр тяжести тонкого круглого однородного стержня изогнутого по дуге окружности. Размеры стержня указаны на рисунке.

Геометрическая модель решения задачи по статике.

Решение:

Плоскость, в которой лежит окружность радиуса R, является плоскостью симметрии тела. Мы примем ее за координатную плоскость хОу. Тогда будем иметь z_c=0. Кроме того того, тело имеет ось симметрии, расположенную в плоскости и направленную по биссектрисе угла 2α.

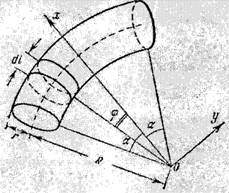
Рис. 1. Геометрическая модель тонкого круглого однородного стержня изогнутого по дуге окружности

Принимая эту ось ось за ось абсцисс, заключаем, что y_c=0. Выбрав начало координат в центре окружности радиуса R, вычислим абсциссу центра тяжести тела.

Выделим элементарный цилиндр с длиной образующей dl. Его объем равен

dv=πr2dl=πr2Rвφ,

 а абсцисса его центра тяжести равна

x=Rcosφ

При решении задач на равновесие твердого тела при наличии сил трения следует выполнить:

1. Выделить твердое тело, равновесие которого надо рассмотреть для отыскания неизвестных величин.

2. Изобразить активные силы.

3. Если твердое тело несвободно, то применив закон освобождаемости от связей, приложить к нему соответствующие реакции связей.

4. Рассмотреть равновесие данного несвободного твердого тела. как тела свободного, находящегося под действием активных сил и реакций связей.

При этом следует реакцию шероховатой поверхности представить двумя составляющими – нормальной реакцией и силой трения, или же двумя составляющими – нормальной реакцией и силой трения, или же, не раскладывая эту реакцию на составляющие, направить ее под углом трения к нормали к поверхности (при максимальной силе трения).

5. Сопоставить число неизвестных величин и число независимых уравнений равновесия, которые должны быть равны для статически определимых задач; при этом к уравнениям равновесия твердого тела следует добавить зависимость силы трения от нормального давления;

6. Выбрать систему координат.

7. Составить систему уравнений равновесия для сил, приложенных к твердому телу или к системе твердых тел.

8. Решив систему уравнений равновесия, определить искомые величины.

Таким образом, мы пришли к результату, выраженному формулой (2). Сопоставляя оба решения, мы видим, что в первом случае мы применили общий метод составления уравнений равновесия для твердого тела, находящегося под действием произвольной плоской системы сил, не учитывая особенностей данной задачи. Достоинство общих методов и заключается в том, что они ведут к цели, несмотря на различия в условиях задач.

Иногда такой путь не является самым простым и коротким. На примере второго способа решения мы видим, что при учете особенностей данной задачи удалось составить меньшее число уравнений равновесия, которые проще и скорее привели к цели.

На основе разработанного алгоритма решения задачи по статике составим Паскаль-программу.

Program Statika;

Var

x, y, a, Pmin, Pmax:Real;

R:Integer;

Begin

Writeln('vvedite ves sterchnya');

Readln(dv);

Writeln('vvedite dliny sterchnya');

Rreadln(dl);

Writeln('vvedite ugol');

Readln(φ); {φ=60}

Pmin:=(R*(((cos(φ)*3.14/180)/cos(φ)*3.14/180)+y)); {minimalnaya velichina gruza}

Pmax:=(R*(((cos(a)*3.14/180)/cos(φ)*3.14/180)-y)); {maximalnaya velichina gruza}

{pri cos(φ)<y sila xmax ne suschestvuet}

Begin

If xmax<0 then x:=xmin+xmax;

If xmax>0 then x:=Pmin-xmax;

End;

Writeln('xmin=',xmin:8:6);

Writeln('xmax=',xmax:8:6);

Writeln('x=',x:8:6);

Readln;

End.

2.2. ЗАДАЧИ КИНЕМАТИКИ, РЕШАЕМЫЕ ПОСРЕДСТВОМ ЯЗЫКА ПАСКАЛЬ

Скорости точек плоской фигуры могут быть определены аналитическими , графическими или же графоаналитическими методами.

Аналитический метод. При аналитическом методе должны быть заданы уравнения движения плоской фигуры (рис.2)

Хo₁=f ₁(t) , Yо₁ =f ₂(t) , φ = f₃ (t). (1*)

Проекции скорости точки М на неподвижные оси координат определяется равенствами:

V_x=Vо₁Х-W _z(Y-Yo₁)  (2*)

V_y=Vо₁Y + W_z (Х-Хo₁)  (3*)

В этих формулах V_x , V_y – искомые проекции скорости точки М на неподвижные оси координат; Vо₁x = Хo₁ , Vо₁y = Yo₁-проекции скорости полюса, начала подвижной системы координат ХY на неподвижные оси координат ; W_z =φ -проекция угловой скорости на ось Z , перпендикулярную к плоскости движения ;ХУ координаты точки М в неподвижной системе координат ; Хо₁ ,Yо₁ – координаты полюса О₁ в неподвижной системе осей. Определение координат Х ,Y точки М , по заданным уравнениям движения плоской фигуры (1*) производится по формулам:

Х=Хо₁+Х₁ cosφ – Y₁sin φ

Y= Yо₁+ Х₁ sin φ +Y₁ cos φ

Проекции скорости точки М на неподвижные оси координат находятся по формулам:

Vx₁ =Vo₁ x cos φ + Vo₁ у sin φ – Wzy₁ (4*)

Vу ₁= -Vo₁ x sin φ + Vo₁ у сos φ – Wz х₁ (5*)

В этих формулах Vx , Vу- искомые проекции скорости точки М на оси х, у подвижной системы координат , жестко связанной с плоской фигурой ; х у – координаты точки М в подвижной системе осей , остальные величины имеют то же значение , что и в уравнениях (2*) , (3*).

Величины скорости точки М по известным проекциям определяются формулой:

V= √Vx ²+ Vу² =√ Vx₁² + Vу₁² (6*)

Направляющие косинусы даются равенствами:

cos (V,X)= Vx/V , cos (V,У)= Vy/V (7*)

cos (V,X)= Vx/V , cos (V,У)= Vy/V (8*)

Графоаналитические методы. Первый графоаналитический способ определения скоростей точек плоской фигуры основан на формуле распределения скоростей (рис.2).

 

 

 

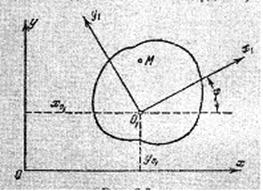
Рис. 2. Геометрическая модель плоской фигуры

V=Vo₁+W r , (9*)

в этой формуле

V – искомая скорости точки М;

Vo₁ - скорость полюса О,

W - угловая скорость плоской фигуры;

r - радиус-вектор , проведенный из полюса О в Рис. 3 точку М.

Таким образом, зная скорость какой-либо точки плоской фигуры, выбираем эту точку за полюс. Далее откладываем от точки М, скорость которой подлежит определению, вектор, равный скорости полюса, и вектор W r₁, направлен перпендикулярно к r₁, и равный по величине W r₁.Векторная сумма этих слагаемых и дает искомую скорость точки М, Если скорость точки М известна по направлению, то можно не знать величины вращательной скорости W r₁, так как и эта скорость, и искомая скорость точки М определяется пересечением прямой, совпадающей с направлением скорости точки М, и прямой, перпендикулярной к линии О М, проведенной из конца вектора Vо, отложенного из точки М.

После того, как треугольник или параллелограмм скоростей выражающий равенство (9*), построен, задача может считаться решенной. Величина и направление скорости точки М могут быть найдены по рис.(2) или получены из решения этого треугольника.

Формула распределения скоростей (9*)записывается часто в виде:

V_b=V_a+V_ba (9**)

где V-искомая скорость точки В, V_a-известная скорость точки А , избранной за полюс, а

V_ba= W АВ, V_ba = W AB, (9***)

- вращательная скорость точки В вокруг точки А, равная по модулю, произведению мгновенной угловой скорости плоской фигуры на расстояние от точки до полюса и направленная перпендикулярно к отрезку прямой ВА в сторону мгновенного вращения фигуры.

Многие задачи могут быть решены при помощи теоремы о равенстве проекции скоростей концов отрезка плоской фигуры на направление отрезка.

Второй графоаналитический метод определения скоростей плоской фигуры основан на использовании мгновенного центра скоростей этой фигуры. При не поступательном движении плоской фигуры (W=0) в каждый данный момент существует точка тела , скорость которой равна нулю. Эта точка называется мгновенным центром скоростей и обычно обозначается через P. Единственным исключением является случай так называемого мгновенно поступательного движения (W=0), который будет рассмотрен отдельно. Выбирая мгновенный центр за полюс, имеем закон распределения скоростей в плоской фигуре.

V=W r ₁, V=W М Р , (10*)

где V-искомая, скорость произвольной точки М; W-угловая скорость плоской фигуры, r₁-радиус-вектор, проведенный из мгновенного центра скоростей в точку М, называемый мгновенным радиусом. Таким образом, скорости всех точек плоской фигуры являются в данный момент вращательными скоростями вокруг мгновенного центра скоростей. Их величина равна произведению величин угловой скорости на модуль мгновенного радиуса, а направлены они перпендикулярно к мгновенному радиусу. Таким образом, величина скоростей точки плоской фигуры пропорциональны величине мгновенных радиусов:

V_b / ВР=V_a / АР=...=W,  (11*)

При графоаналитических методах решения задач рекомендуется такая последовательность действий:

1)        Выбрать за полюс ту точку плоской фигуры, направление скорости которой известно;

2)        найти другую точку плоской фигуры, направление скорости которой известно;

1)        пользуясь формулой распределения скоростей, найти скорость этой точки плоской фигуры;

2)        исходя из формулы распределения скоростей определить значение угловой скорости плоской фигуры в данный момент времени;

3)        зная угловую скорость фигуры и скорость полюса, найти с помощью формулы распределения скоростей искомые скорости других точек фигуры.

При графоаналитическом методе решения задач может быть применен метод проекции. В этом случае может быть рекомендован следующий порядок решения задач:

1. Выбрать за полюс точку плоской фигуры, скорость которой известна;

2. Пользуясь формулой распределения скоростей, построить скорость другой точки плоской фигуры, у которой известно направление ее скорости;

3. Спроектировать полученный треугольник скоростей на направление прямой, соединяющей обе точки, и найти скорость второй точки;

4. Спроектировать треугольник скоростей на направление, перпендикулярное к прямой, соединяющей обе точки, и найти вращательную скорость второй точки по отношению к полюсу;

5. Разделив вращательную скорость на расстояние от точки до полюса, найти мгновенную угловую скорость плоской фигуры;

6. Зная мгновенную угловую скорость фигуры, можно найти скорости любых точек плоской фигуры, пользуясь формулой распределения скоростей.

Если задача решается при помощи мгновенного центра скоростей, рекомендуется такая последовательность:

1)        определить положение мгновенного центра плоской фигуры;

2)        найти величину мгновенного радиуса той точки плоской фигуры, скорость которой известна и определить угловую скорость плоской фигуры, разделив величину скорости точки на величину мгновенного радиуса;

3)    найти искомые величины скоростей точек плоской фигуры, умножая угловую скорость на мгновенный радиус соответствующей точки или используя.

Теперь рассмотрим конкретную задачу по кинематике.

Задача. Для преобразования периодического возвратно-поступательного движения во вращательное движение в двигателях внутреннего сгорания применяют шатунно-кривошипный механизм, состоящий из кривошипа ОА=r, вращающегося вокруг неподвижной точки О в плоскости рисунка, шатуна АВ=l, шарнирно соединенного с кривошипом, и поршня В, двигающегося по горизонтальным направляющим цилиндра, совпадающим с прямой ОВ.

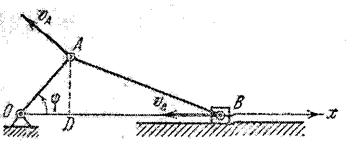
Рис. 3. Геометрическая модель плоского шатунно-кривошипного механизма

На основе разработанного алгоритма решения задачи по кинематике составим Паскаль – программу.

Program Kinematika;

Var t,f0,k,b1,b2,x1,x2,a,b,l,d,f1,f2,a1,a2,w1,w:real;

Begin

Write('vvedite welichini a b d l w t = ');

Readln(a,b,d,l,w,t);

x1:=(sqr(d+b)-a*a+l*l)/(2*l*(d+b));

f1:=(180/pi)*arctan(sqrt(1-sqr(x1))/x1);

x2:=(sqr(d+b)-a*a-l*l)/(2*l*a);

a1:=(180/pi)*arctan(sqrt(1-sqr(x2))/x2);

x1:=-(l*l+sqr(d-b)-a*a)/(2*l*(d-b));

f2:=(180/pi)*arctan(sqrt(1-sqr(x1))/x1);

x2:=(l*l-sqr(d-b)+a*a)/(2*l*a);

a2:=(180/pi)*arctan(sqrt(1-sqr(x2))/x2);

f0:=w*t;

k:=sqrt(l*l+b*b-2*l*b*cos(f0));

x1:=(k*k+d*d-a*a)/(2*k*d);

b2:=arctan(sqrt(1-sqr(x1))/x1);

x2:=(1/k)*sin(f0);

b1:=arctan(x2/sqrt(1-sqr(x2)));

w1:=(b*k*sin(b1+b2)*w)/(a*a*sin(b2));

Writeln('a1= ', a1:6:3,' a2= ',a2:6:3);

Writeln('f1= ', f1:6:3,' f2= ',f2:6:3);

Writeln('w1= ',w1:6:3);

Readln;

End.