Навигация
Статистика распределения цветов (в различных представлениях, в том числе гистограмма изображения);
1. Статистика распределения цветов (в различных представлениях, в том числе гистограмма изображения);
2. Статистические моменты (среднее, дисперсия, скрытые Марковские модели);
Количество и свойства графических примитивов в объекте (прямых линий, окружностей – для распознавания символов) (на основе преобразования Хафа) 2.1. Метод наименьших квадратовПеред тем, как начинать рассмотрение МГУА, было бы полезно вспомнить или узнать впервые метод наименьших квадратов — наиболее распространенный метод подстройки линейно зависимых параметров.
Рассмотрим для примера МНК для трех аргументов:
Пусть функция T=T(U, V, W) задана таблицей, то есть из опыта известны числа Ui, Vi, Wi, Ti ( i = 1, … , n). Будем искать зависимость между этими данными в виде:
(ф. 1)
где a, b, c — неизвестные параметры.
Подберем значения этих параметров так, чтобы была наименьшей сумма квадратов уклонений опытных данных Ti и теоретических Ti = aUi + bVi + cWi, то есть сумма:
(ф. 2)
Величина s является функцией трех переменных a, b, c. Необходимым и достаточным условием существования минимума этой функции является равенство нулю частных производных функции s по всем переменным, то есть:
(ф. 3)
Так как:
(ф. 4)
то система для нахождения a, b, c будет иметь вид:
(ф. 5)
Данная система решается любым стандартным методом решения систем линейных уравнений (Гаусса, Жордана, Зейделя, Крамера).
Рассмотрим некоторые практические примеры нахождения приближающих функций:
1. y = ax2 + bx + g
Задача подбора коэффициентов a, b, g сводится к решению общей задачи при T=y, U=x2, V=x, W=1, a=a, b=b, g=c.
2. f(x, y) = asin(x) + bcos(y) + g/x
Задача подбора коэффициентов a, b, g сводится к решению общей задачи при T=f, U=sin(x), V=cos(y), W=1/x, a=a, b=b, g=c.
Если мы распространим МНК на случай с m параметрами,
(ф. 6)
то путем рассуждений, аналогичных приведенным выше, получим следующую систему линейных уравнений:
(ф. 7)
где , 2.2. Моделирование многомерной функции распреде ления векторов признаков изображений объекта Факторный Анализ(FA)Факторный анализ (ФА), как и многие методы анализа многомерных данных, опирается на гипотезу о том, что наблюдаемые переменные являются косвенными проявления относительно небольшого числа неких скрытых факторов. ФА, таким образом, это совокупность моделей и методов ориентированных на выявление и анализ скрытых (латентных)зависимостей между наблюдаемыми переменными. В контексте задач распознавания, наблюдаемыми переменными обычно являются признаки объектов.
Модели с латентными переменными применяются при решении следующих задач:
· понижение размерности признакового пространства,
· классификация объектов на основе сжатого признакового пространства,
· косвенной оценки признаков, не поддающихся непосредственному измерению,
· преобразование исходных переменных к более удобному для интерпретации виду.
Факторный анализ использует предположение о том, что исходные наблюдаемые переменные (распределенные по нормальному закону!) xi могут быть представлены в виде линейной комбинации факторов, также распределенных нормально:
xi=∑k=1..m(aikFk) + ui; i=1,...,n;
В этой модели присутствуют две категории факторов: общие факторы (common factors) Fk и специфические факторы(unique factors) ui. Фактор называется общим, если он оказывает влияние на две и более наблюдаемые переменные (математически это выражается в наличии как минимум двух существенно отличающихся от нуля коэффициентов aik для данного фактора Fk). Каждый из специфических факторов ui несет информацию только об одной переменной xi. Матрица aik называется матрицей факторных нагрузок (factor loadings) и задает влияние общих факторов на наблюдаемые переменные.
Содержательно, специфические факторы соответствуют необъясненной общими факторами изменчивости набора наблюдаемых переменных. Таким образом их можно рассматривать как случайную ошибку наблюдения или шум, не являющийся ценной информацией для выявления скрытых закономерностей и зависимостей. Важным предположением является независимость ui между собой. Обычно, однако не всегда, общие факторы Fk предполагаются некоррелированными (ортогональными).
Важными понятиями ФА являются общность и специфичность наблюдаемой переменной. На языке ФА доля дисперсии отдельной переменной, принадлежащая общим факторам (и разделяемая с другими переменными) называется общностью, дисперсия же приходящаяся на специфический фактор - специфичностью.
Целью ФА является выявление общих факторов Fk, специфических факторов ui и матрицы факторных нагрузок A таким образом, чтобы найденные общие факторы объясняли наблюдаемые данные наилучшим образом, то есть чтобы суммарная общность переменных была максимальна (а соответственно специфичность - минимальна).
Отличие Факторного Анализа (Factor Analysis, FA) от Метода Главных Компонент (Principal Components Analysis, PCA)
· Результатом ФА является модель, в явном виде описывающая зависимость наблюдаемых переменных от скрытых факторов (МГК это описательный анализ данных, без получения модели);
· ФА предусматривает ошибку моделирования (специфический фактор) для каждой из наблюдаемых переменных, в то время как МГК пытается объяснить всю изменчивость, включая шум, зависимостью от главных компонент;
· В МГК главные компоненты являются линейными комбинациями наблюдаемых переменных. В ФА наблюдаемые переменные являются линейными комбинациями общих и специфических факторов;
· Получаемые в результате ФА факторы могут быть использованы для интерпретации наблюдаемых данных;
· Главные компоненты некоррелированны (что эквивалентно их ортогональности при переносе начала координат в центр масс исходного набора), факторы же - не обязательно;
· МГК можно рассматривать как частный случай ФА, когда все специфические факторы приняты равными нулю, а общие факторы ортогональны.
Метод главных компонент(PCA)Метод главных компонент применяется для снижения размерности пространства наблюдаемых векторов, не приводя к существенной потере информативности. Пусть дан исходный набор векторов линейного пространства Rn. Применение метода главных компонент позволяет перейти к базису пространства Rn, такому что:
Первая компонента (первый вектор базиса) соответствует направлению, вдоль которого дисперсия векторов исходного набора максимальна. Направление второй компоненты (второго вектора базиса) выбрано таким образом, чтобы дисперсия исходных векторов вдоль него была максимальной при условии ортогональности первому вектору базиса. Аналогично определяются остальные векторы базиса.
В результате, направления векторов базиса выбраны так, чтобы максимизировать дисперсию исходного набора вдоль первых компонент, называемых главными компонентами (или главными осями). Получается, что основная изменчивость векторов исходного набора векторов представлена несколькими первыми компонентами, и появляется возможность, отбросив оставшиеся (менее существенные) компоненты, перейти к пространству меньшей размерности.
Результатом применения МГК является вычисление матрицы W размера m x n, осуществляющей проекцию векторов пространства Rn на подпространство, натянутое на главные компоненты:
y = Wt(x - μ), y ![]() Rm, x
Rm, x ![]() Rn.
Rn.
Где x - вектор из исходного набора, y - координаты вектора в подпространстве главных компонент, μ - средний вектор начального набора.
Главные компоненты (векторы базиса), выбираемые с помощью МГК, обладают следующим свойством: обратная проекция вектора y в Rn дает минимальную ошибку реконструкции (минимальное расстояние до образа вектора y). Нужно отметить, что корректное применение МГК возможно лишь при предположении о нормальном распределении векторов исходного набора.
В приложении к задаче классификации с учителем МГК обычно применяется следующим образом. После вычисления главных осей тренировочного набора, вектор признаков тестового объекта проецируется на подпространство, образованное главными осями. Вычисляются две характеристики: расстояние от проекции тестового вектора до среднего вектора тренировочного набора - Distance in Feature Space (DIFS), и расстояние от тестового вектора до его проекции в подпространство главных компонент - Distance From Feature Space (DFFS). Исходя из этих характеристик выносится решение о принадлежности тестового объекта классу, образованному тренировочным набором.
Отличие Факторного Анализа (Factor Analysis, FA) от Метода Главных Компонент (Principal Components Analysis, PCA)
· Результатом ФА является модель, в явном виде описывающая зависимость наблюдаемых переменных от скрытых факторов (МГК это описательный анализ данных, без получения модели);
· ФА предусматривает ошибку моделирования (специфический фактор) для каждой из наблюдаемых переменных, в то время как МГК пытается объяснить всю изменчивость, включая шум, зависимостью от главных компонент;
· В МГК главные компоненты являются линейными комбинациями наблюдаемых переменных. В ФА наблюдаемые переменные являются линейными комбинациями общих и специфических факторов;
· Получаемые в результате ФА факторы могут быть использованы для интерпретации наблюдаемых данных;
· Главные компоненты некоррелированы (что эквивалентно их ортогональности при переносе начала координат в центр масс исходного набора), факторы же - не обязательно;
· МГК можно рассматривать как частный случай ФА, когда все специфические факторы приняты равными нулю, а общие факторы ортогональны.
Анализ независимых компонент(ICA). Начало формы Конец формыЗадачей анализа независимых компонент (Independent Components Analysis, ICA) является разложение наблюдаемых случайных переменных xj в линейную комбинацию независимых случайных величин sk:
xj=aj1s1+aj2s2+...+ajnsn для всех j.
Основными предположениями, используемыми в данном методе, являются независимость компонент sk и, то, что их распределение отлично от нормального (non-gaussian). Алгоритм вычисления независимых компонент опирается на центральную предельную теорему, утверждающую, что при определенных условиях сумма независимо распределенных случайных величин стремится к нормальному распределению по мере увеличения количества слагаемых. Использую это утверждение, поиск независимых компонентов, как линейных комбинаций наблюдаемых переменных, ведется таким способом, чтобы получить независимые случайные величины, распределение которых максимально далеко от нормального. Степень близости распределения случайной величины к нормальному измеряется различным способами [Hyvarinen2000].
По своей формулировке, ICA близок к методу главных компонент (PCA) и факторному анализу (FA), однако имеет ряд существенных различий:
· В ICA существенно используется предположение о том, что распределения независимых компонент отличны от нормального,
что дает возможность интерпретировать ICA как FA для неортогональных факторов, с распределением отличным от нормального;
· В ICA понижение размерности не является целью, в отличии от FA и PCA;
· PCA добивается того, чтобы проекции векторов исходного набора на оси главных компонент были некоррелированы, в то время как ICA добивается их независимости (более сильное условие);
· Оси PCA ортогональны, в то время как оси независимых компонент - необязательно;
Линейный Дискриминантный Анализ (Linear Discriminant Analysis, LDA) Линейный Дискриминантный Анализ, в отличие от МГК и ФА не ставит своей целью найти подпространство меньшей размерности, наилучшим образом описывающее набор тренировочных изображений. Его задача - найти проекцию в пространство, в котором разница между различным классами объектов максимальна. Это требование формулируется как получение максимально компактных кластеров, соответствующих различным классам, удаленных на максимально возможное расстояние. С помощью ЛДА удается получить подпространство небольшой размерности, в котором кластеры изображений пересекаются минимально. Производить классификацию в таком пространстве значительно проще. 2.3. Деформируемые моделиНачало формы
Конец формы
В машинном зрении деформируемые модели являются мощным инструментом анализа и обработки данных. Деформируемые модели, в отличии от жестких (rigid), обладают большой гибкостью (имеют возможность представлять объекты с сильно различающейся формой) и в то же время дают возможность указать достаточно строгие ограничения на нежелательные изменения формы представляемых объектов.
В качестве примеров использования деформируемых моделей можно привести:
· выделение (локализация) объектов и структур определенного вида на 2D и 3D изображениях (черт человеческого лица, объектов на медицинских изображениях)
· отслеживания перемещения объектов между кадрами видеопотока.
· сегментация 2D и 3D изображений
· гладкая аппроксимации разреженного облака точек
· реконструкции 3D формы объекта по 2D изображениям - с помощью стерео, восстановления формы по закраске (shape from shading)
Использование деформируемых моделей при решение задачи обработки и распознавания изображений обычно позволяет в элегантной математической форме описать одновременное воздействие многих (возможно, противоречивых) факторов на процесс получения оптимального решения.
Конкретная деформируемая модель характеризуется:
· Способом задания формы модели (аналитические кривые и поверхности, конечные элементы);
· Способом измерения критерия согласия (goodness of fit) модели и измеренных данных;
Способом модификации формы модели (по каким именно правилам (формулам) происходит изменение формы модели); 2.4. Скрытые Марковские Модели (Hidden Markov Models, HMM) Скрытые Марковские Модели (СММ) являются одним из способов получения математической модели (описания свойств) некоторого наблюдаемого сигнала. СММ относятся к классу стохастических моделей. Стохастические модели пытаются охарактеризовать только статистические свойства сигнала, не обладая информацией о его специфических свойствах. В основу стохастических моделей положено допущение о том, что сигнал может быть описан некоторым параметрическим случайным процессом и что параметры этого процесса могут быть достаточно точно оценены некоторым, вполне определенным способом. Настроенную СММ можно рассматривать как источник некоторого случайного сигнала со вполне определенными характеристиками. Для настроенной СММ есть возможность подсчитать вероятность генерации тестового сигнала данной моделью. В приложении к задаче распознавания, представив вектор признаков объекта в виде сигнала (набора последовательных наблюдений), можно смоделировать класс объектов с помощью СММ. Вероятность принадлежности тестового объекта классу, заданному СММ оценивается как вероятностью генерации сигнала, соответствующего его вектору признаков. Настройка (обучение) СММ - состоит в модификации ее параметров для того, чтобы добиться максимальной вероятности генерации сигналов, соответствующих векторам тренировочного набора. 2.5. Метод Опорных Векторов (Support Vector Machines, SVM)Цель тренировки большинства классификаторов - минимизировать ошибку классификации на тренировочном наборе (называемую эмпирическим риском). В отличие от них, с помощью метода опорных векторов можно построить классификатор минимизирующий верхнюю оценку ожидаемой ошибки классификации (в том числе и для неизвестных объектов, не входивших в тренировочный набор). Применение метода опорных векторов к задаче распознавания заключается в поиске гиперплоскости в признаковом пространстве, отделяющей классы.
Классификация с помощью опорных векторов позволяет использовать аппарат ядерных функций для неявного проецирования векторов-признаков в пространство потенциально намного более высокой размерности (еще выше, чем пространство изображений), в котором классы могут оказаться линейно разделимы. Неявное проецирование с помощью ядерных функций не приводит к усложнению вычислений, что позволяет успешно использовать линейный классификатор для линейно неразделимых классов.3. Реализация программного обеспечения
В ходе работы над бакалаврской работой была написана программа, Выделяющая на изображении искомые объекты и нормирующая их.
Программа представляет собой простое SDI-приложение, написанное в среде Builder C++ v. 6.0. Для реализации обработки изображения использовалась библиотека Intel® Open Source Computer Vision Library (OpenCV).
В программе были использованы следующие функции библиотеки OpenCV:
Функция | Описание функции |
| cvLoadImage | Загружает изображение из файла |
| cvSize | Возвращает размер изображения |
| cvCreateImage | Создает новое изображение |
| cvAbsDiff | Производит вычитание по модулю двух изображений |
| cvCmpS | Бинаризирует изображении, используя порог |
| cvErode | Выполняет побитовую операцию эрозии изображения |
| cvCamShift | Реализует алгоритм сравнения двух изображений |
| cvGetQuadrangleSubPix | Производит аффинное преобразование изображения |
| cvSetZero | Заполняет изображение черным цветом |
| cvFillConvexPoly | Заполняет многоугольник на изображении заданным цветом |
| cvCopy | Копирует изображение |
Также были использованы следующие классы:
| Класс | Описание класса |
| IplImage | Изображение |
| CvSize | Размер матрицы |
| CvPoint | Точка |
| CvRect | Прямоугольник |
| CvBox2D | Прямоугольник |
| CvMat | Матрица |
Алгоритм программы:
Начало → Загружаем изображение-эталон → Отображаем эталон на экране → Ждем щелчка мыши → Загружаем исследуемое изображение → Отображаем эталон на экране → Ждем щелчка мыши → Выполняем вычитание двух изображений → Бинаризируем результат → Отображаем результат на экране → Ждем щелчка мыши → Выполняем эрозию результата → Отображаем результат на экране → Ждем щелчка мыши → Находим минимальный прямоугольник, охватывающий найденные объекты → Поворачиваем исследуемое изображение → Отображаем результат на экране → Ждем щелчка мыши → Нормализуем результат → Отображаем результат на экране → дем щелчка мыши → Конец
Заключение
В работе создана программа обработки изображений. В дальнейшем планируется разработка программного обеспечения для классификации полученных образов.
Похожие работы
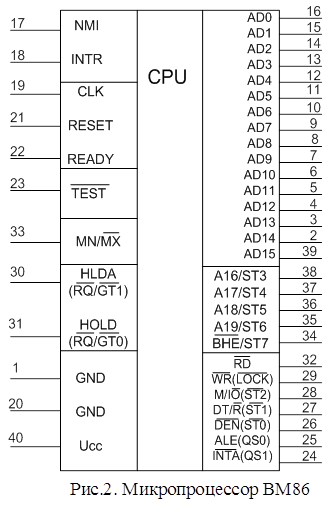
... и описание выводов которых приведено в следующем пункте курсовой работы. Выбор элементной базы Микросхема К1810ВМ86 Микропроцессор К1810ВМ86 представляет собой однокристальный 16-битовый МП работающий в данной вычислительной системе в минимальном режиме. Этот модуль производит чтение ПЗУ, а также чтение и запись в порты ввода-вывода. Условное графическое обозначение МП К1810ВМ86 ...
... также невысока и обычно составляет около 100 кбайт/с. НКМЛ могут использовать локальные интерфейсы SCSI. Лекция 3. Программное обеспечение ПЭВМ 3.1 Общая характеристика и состав программного обеспечения 3.1.1 Состав и назначение программного обеспечения Процесс взаимодействия человека с компьютером организуется устройством управления в соответствии с той программой, которую пользователь ...
... (САПР) и пр.; - ПС, используемые в обучении – электронные учебники, тренажеры, тесты и пр.; - игровые программы; - программы, созданные пользователем с помощью сред программирования. Еще один класс программного обеспечения – специальное ПО. Основное его отличие от системного ПО в том, что пользователь сам решает, будет ли он использовать эти ПС или нет, а отличие ...
... продукт предназначается для передачи информации о конструкции печатной платы из пакета PCAD в T-FLEX по сквозному маршруту проектирования для выработки дальнейших конструкционных решений и разработки деталей оснастки. 1. Состав программного обеспечения: · p-flex.exe : основной файл, осуществляющий всю работу; · gabarits.dbf : база данных в виде таблицы, куда заносятся все найденные ...




0 комментариев