Навигация
Программный кодер-декодер для циклических (n,k)-кодов
Кафедра Автоматики и Информационных Технологий
Лабораторная работа
"ПРОГРАММНЫЙ КОДЕР-ДЕКОДЕР ДЛЯ ЦИКЛИЧЕСКИХ (n, k) – КОДОВ"
1. Преследуемые цели
Проведение лабораторных работ по данной тематике преследует следующие цели:
- закрепление теоретического материала, касающегося основных положений математической теории линейных (n, k) – кодов;
- осознание механизма кодирования пакетов данных при передаче файлов;
- практическое освоение алгоритмов кодирования и декодирования применительно к циклическим (n, k) – кодам.
2. Необходимые сведения из теории
Известно, что циклические коды из всех помехоустойчивых кодов находят наибольшее применение на практике.
Циклические коды представляют собой подкласс (подмножество) линейных (n, k) – кодов. Это значит, что все положения теории, которые справедливы для нециклических линейных (n, k) – кодов, справедливы и для кодов циклических. Но циклические коды обладают рядом дополнительных положительных свойств, в частности, они «остро реагируют» на близко расположенные в кодовом слове ошибки, так называемые «пачки ошибок». Кроме того, для них найдены чрезвычайно простые алгоритмы кодирования и декодирования. Все это и обеспечило им широкое применение на практике. Их применение оговорено многими международными стандартами, регламентирующими работу каналов передачи.
Для описания циклических кодов параллельно используется представление кодовых слов и двоичным вектором, и многочленом от некоторой формальной переменной x. Постоянно приходится переходить от одной формы представления к другой. Одну и ту же двоичную последовательность обозначим V, если она рассматривается как вектор, или V(x), если она интерпретируется как многочлен.
2.1 Конструктивное определение циклического (n, k) – кода
Циклическим (n, k) – кодом называется множество многочленов степени не больше (n‑1), каждый из которых нацело делится на (специально подобранный) порождающий многочлен G(x) степени (n-k), являющийся делителем бинома xn+1.
Циклический код со словами длины n и с порождающим многочленом G(x) существует тогда и только тогда, когда G(x) делит xn+1[1]. В лекционном курсе было показано, что это требование делимости бинома xn+1 на G(x) вытекает из специфики определения операции символического умножения многочленов (по модулю бинома xn+1). Для того, чтобы максимизировать множество слов порождаемого кода при фиксированных значениях длины слов n и кодового расстояния d0, многочлен G(x) должен быть неприводимым делителем степени (n-k).
2.2 Алгоритм кодирования
На практике чаще всего применяется алгоритм кодирования, который формирует систематический разделимый код. В основу такого алгоритма положена операция деления на G(x). Систематические разделимые коды привлекательны тем, что процедуру кодирования, т.е. преобразования информационного вектора A (длины k) в вектор кода V (длины n>k) удается свести лишь к формированию (n-k) контрольных бит.
Шаг 1. Предварительно вектор A «отнормируем по формату» под длину n, воспользовавшись операцией умножения многочленов A(x)×xn-k. Как было показано в лекционном курсе – это эквивалентно сдвигу вектора A на (n-k) позиций влево. Произведение многочленов на языке векторов имеет длину n. Существенно для последующего, что правые (n-k) позиций оказываются непременно нулевыми.
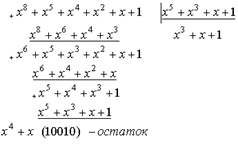
Шаг 2. Произведение A(x)×xn-k разделим на G(x). Ясно, что в общем случае оно не обязано делиться на G(x) нацело. Поэтому следует записать
A(x)×xn-k=Q(x)×G(x)+R(x),
где Q(x) - частное от деления;
R(x) - остаток. Это многочлен степени не больше (n-k‑1), т. к. делитель имеет степень (n-k) по определению. Как вектор он имеет длину (n-k).
Шаг 3. Перенесём остаток R(x) в левую часть равенства. Получим:
A(x)×xn-k+R(x)=Q(x)×G(x).
Теперь в левой части мы получаем многочлен, который нацело делится на G(x), а это по определению – многочлен, принадлежащий циклическому (n, k) – коду. В этой последней операции остаток R складывается с нулями (см. шаг1 алгоритма). Следовательно, конечный итог эквивалентен конкатенированию R к вектору А.
2.3 Алгоритм декодирования
Известно несколько алгоритмов декодирования циклических (n, k) – кодов. В данной лабораторной работе исследуется «декодирование по синдрому», роль которого (синдрома) играет остаток от деления декодируемого многочлена F(x) на G(x). Декодирование может производиться с целью только обнаруживать ошибки или с целью исправлять ошибки кратности до t включительно. В любом случае цель достигается в несколько шагов алгоритма.
2.3.1 Декодирование с обнаружением ошибок
Шаг 1. Вычисление остатка R(x);
Шаг 2. Анализ остатка «на ноль». Нулевой остаток означает, что ошибки не обнаружены;
2.3.2 Декодирование с исправлением ошибок
Шаг 1. Вычисление остатка R(x);
Шаг 2. Вычисление по найденному остатку предполагаемого (наиболее вероятного) многочлена ошибки Е(х);
Шаг 3. Исправление декодируемого вектора F путем суммирования F+E=V;
Похожие работы
... , если его длина n=qm-1 над GF(q). Если длина кода меньше длины примитивного кода, то код называется укороченным или непримитивным. Общее свойство кодовых слов циклического кода - это их делимость без остатка на некоторый многочлен g(x), называемый порождающим. Результатом деления двучлена xn+1 на многочлен g(x) является проверочный многочлен h(x). При декодировании циклических кодов используются ...
... также невысока и обычно составляет около 100 кбайт/с. НКМЛ могут использовать локальные интерфейсы SCSI. Лекция 3. Программное обеспечение ПЭВМ 3.1 Общая характеристика и состав программного обеспечения 3.1.1 Состав и назначение программного обеспечения Процесс взаимодействия человека с компьютером организуется устройством управления в соответствии с той программой, которую пользователь ...
... информация должна поступать в декодер при восстановлении звукового сигнала. Декодер преобразует серию сжатых мгновенных спектров сигнала в обычную цифровую волновую форму. Audio MPEG - группа методов сжатия звука, стандартизованная MPEG (Moving Pictures Experts Group - экспертной группой по обработке движущихся изображений). Методы Audio MPEG существуют в виде нескольких типов - MPEG-1, MPEG-2 и ...
... приложении 1. Кодер позволяет получить контрольные символы по информационным. Схема составлена в полном соответствии с выражениями (9) и матрицей (10). Декодер соответствует матрице (11). В приложении 2 приведена схема всей системы передачи данных. Исходный код (11 байт) подаётся на регистр REG1. Это можно сделать, например, трёхкратной передачей по 32 разряда (4 байта). Регистр может быть также ...
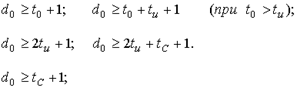
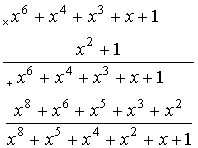
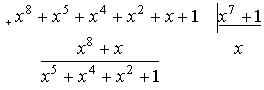






0 комментариев