Защита результатов, отчет по лабораторной работе

6. Защита результатов, отчет по лабораторной работе

Результаты работы программы DECODER должны быть продемонстрированы преподавателю. Отчет должен содержать краткое изложение постановки задачи, требуемые параметры выходного кода, граф-схему алгоритма работы основного декодирующего модуля с комментариями, объем и результаты тестового декодирования (например, в табличной форме) с подробными комментариями.

 

7. Быстрый кодер / декодер для циклических кодов

Применение быстрого алгоритма в лабораторной работе не является обязательным для всех. Он может быть использован по желанию студентов или по прямому указанию преподавателя.

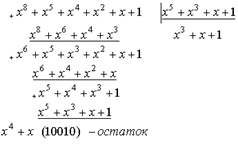
Выше говорилось, что при циклическом кодировании основной операцией алгоритмов кодирования входной последовательности А(х) и декодирования выходной является операция деления выражения А(х) х^(n-k) на порождающий многочлен с целью нахождения остатка, который суммируется с А(х) х^(n-k) по mod2.

Трудность программной реализации кодирующих и декодирующих модулей для циклических кодов состоит в том, что алгоритмы, обычно, предусматривают процедуру многократно повторяемого «битового деления». Время кодирования /декодирования часто оказывается неприемлемым. Далее излагается математическая суть алгоритма деления двоичных последовательностей, позволяющего выполнять деление по частям. «Крупностью» частей в известных пределах можно варьировать, добиваясь оптимизации процедуры в конкретных условиях.

7.1 Алгоритм деления по частям

Разобьем k‑битовую последовательность А, выраженную многочленом А(х), на ℓ‑битовые отрезки (блоки). Так как в общем случае k не обязано быть кратным ℓ, входная последовательность будет поделена на s блоков, из которых последний имеет длину m₀<ℓ. Выполняется условие: k=ℓ (s‑1)+m₀.

Шаг 1

Выделим в последовательности А левые ℓ бит. Пусть в символике многочленов они выражаются многочленом А₁(х), а оставшуюся (справа) часть обозначим А`₁(х).

Тогда входную последовательность А(х) можно представить в форме:

А(х)=А₁(х) х^(k-ℓ) +А`₁(х). (1)

(Здесь и далее суммирование двоичных многочленов и векторов ведется по mod2).

Делимое А(х) х^(n-k) в алгоритме кодирования запишем как

 

А(х) х^(n-k) =(А₁(х) х^(k-ℓ) +А`₁(х)) х^(n-k) (2)

Векторная иллюстрация к шагу 1.

При ℓ=4, k=11 (одиннадцать) пусть А=1101 1000 110. Здесь m₀ =3, А₁=1101.

А₁(х) х^(k-ℓ) в векторной форме выглядит как 1101 0000000, так как умножение на х^(k-ℓ) эквивалентно приписыванию справа (k-ℓ) нулей. А`<sub>1</sub>=1000 110. Сумма А<sub>1</sub>(х) х<sup>(k-ℓ)</sup> +А`₁ =А(х) выглядит как

1101 0000000

1000110 ^Å

1101 1000110

В выражении (2) первый член суммы в круглых скобках умножим и разделим на порождающий многочлен и произведем умножение обоих членов на х^(n-k). Получим:

(3)

Дробь  представим как меньшую целую часть (частное) Q₁(х), которое в конечном итоге нас не интересует, плюс остаток от деления R₁(х). С учетом этого перепишем (3).

Получим:

А(х) х^(n-k) =Q₁(х) G(x) х^(k-ℓ) +R₁(x) х^(k-ℓ)+А`₁(х) х^(n-k) (4)

Старшая степень многочлена  не превосходит (ℓ-1), т. к. такую степень по соглашению имеет А₁(х), а G(x) имеет фиксированную степень (n-k) по определению (вывернутые полускобки символизируют ближайшее меньшее целое от дроби, т.е. частное). Тогда получается, что первое слагаемое в (4) имеет старшую возможную степень (n‑1), что соответствует вектору длины n.

Старшая степень остатка R₁(x) не превосходит величины (n-k‑1), а всего второго слагаемого в (4) – величины (n-ℓ-1). Такую же степень имеет и третье слагаемое А`₁(х) х^(n-k). Сложим эти два последних члена, сумму обозначим F₁(х). Перепишем (4) в следующем виде:

 

А(х) х^(n-k) =Q₁(х) G(x) х^(k-ℓ) +F₁(х) (5)

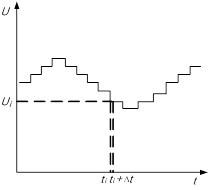
Рис. 1 иллюстрирует формирование последовательности F₁ в векторной интерпретации всех участвующих величин. Обратим внимание на длину последовательности F₁, на то обстоятельство, что при суммировании векторы R₁ и A`₁ «выровнены» со стороны старших разрядов, а F₁ имеет справа (n-k) нулевых бит.

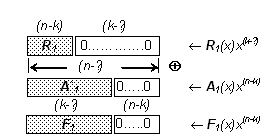
Рис. 1. Формирование последовательности F₁ при векторном представлении величин

На этом первый шаг алгоритма деления по частям закончен. Получен F₁(х), куда вошел первый промежуточный остаток R₁(x), контролирующий деление первого блока из ℓ левых бит входной последовательности А(х).

Шаг 2

Очередной шаг алгоритма заключается в том, что в F₁(х) выделяем ℓ левых бит. Этот отрезок должен быть обозначен А₂(х). Оставшаяся правая часть F₁(х) – это А`₂(х). В соответствии с (3), (4) находим выражение остатка R₂(x) и последовательности F₂(х).

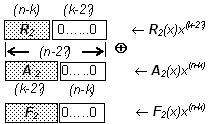
Рис. 2. Формирование последовательности F₂ при векторном представлении величин

На рис. 2 проиллюстрировано получение F₂. Предпринята попытка масштабно отобразить изменение участвующих в деле векторов. Здесь показано, что после второго шага F₂ все еще имеет справа (n-k) нулей. Это эквивалентно допущению, что деление входного вектора А на отрезки длины ℓ двумя шагами не исчерпывается.

Делимое (в его стартовом понимании) после второго шага имеет вид:

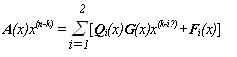(6)

В общем случае, пока (k-iℓ)≥(n-k) вектор F_i должен будет иметь справа (n-k) нулей. Это, как известно, место контрольных бит в словах циклического кодового слова. Они пока не сформированы.

Шаг s‑1

В процессе выполнения (s‑1) – го шага мы оперируем векторами длины (n-k+m₀) (см. рис. 3). К этому времени все отрезки длины ℓ в составе входного вектора будут исчерпаны и (если в общем случае k не делится нацело на ℓ) у нас остаётся от входной последовательности вычисленный остаток R_s-1 и «правый» отрезок A`_s-1 длины m₀<ℓ.

В соответствии с выражениями (4) и (5) получим «выходной продукт» данного шага – многочлен F_s-1(х) = R_s-1(x) x^(k-(s-1)ℓ) + A`<sub>s-1</sub> (х) х<sup>(n-k)</sup> =R<sub>s-1</sub>(x) x<sup>(m0)</sup> + A`_s-1 (х) х^(n-k), т. к. k=(s‑1)ℓ+m₀ по определению этих величин.

Рис. 3. Формирование последовательности F_s-1 при векторном представлении величин

Обозначим последние формирующиеся (n-k) бит Y(х). Как мы видели до (s‑1) – го шага Y(х)=0. Следовательно, Y(х) можно ввести в (6) как нулевое слагаемое, если пределы суммирования ограничить величиной (s-u‑1). После шага s можно записать

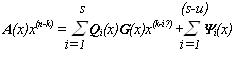(7)

Здесь 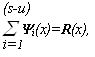 т.е. является проверочными битами кодового слова.