Навигация
Возвращаемся к пункту 2 до тех пор пока не будут перебраны все незанятые точки
4. Возвращаемся к пункту 2 до тех пор пока не будут перебраны все незанятые точки.
Программа
Uses crt;
Const n=9 ;{Количество точек}
m=400;{}
Type tochka=record
x,y,r:real;
n:word;
end;
Mass=array[0..n] of tochka;
Var sch:word;
number:text;
Procedure Sozd_t(Var MT:Mass; n,m:Word);
Var i:word;
Begin randomize;
For i:=1 to n do
begin
MT[i].x:=random(m);
MT[i].y:=random(m);
MT[i].n:=i;
end;
End;
Procedure Sdvyg(Var MT:Mass;n1,n2:word);{n1- n2-}
Var i:word;
Begin
For i:=n1 to n2-1 do MT[i]:=MT[i+1];
MT[n2].x:=1000; MT[n2].y:=1000;
End;
{Сохраняем полученную ломаную}
Procedure Save(MT:mass);
Var i:word;
st1,st2:string[n];
Begin
sch:=sch+1; st2:='';
For i:=1 to n do
begin
Write(MT[i].n,' ');
str(MT[i].n,st1);
st2:=st2+st1;
end;
Writeln('---',sch,'---');
Writeln(number,st2);
readkey;
End;
Procedure Rekurs(MT:Mass;Kol:word;T:word);
Var i,j,g:word;
s:boolean;
Begin
MT[0]:=MT[t];
Sdvyg(MT,t,kol);
MT[kol]:=MT[0];
Kol:=kol-1;
IF kol>0 then
For j:=1 to kol do
begin s:=true;
for i:=kol+1 to n-1 do
if Peres(MT[j],MT[kol+1],MT[i],MT[i+1]) then s:=false;
if s then Rekurs(MT,kol,j)
end
ELSE begin s:=true;
For g:=1 to n-1 do
if Peres(MT[1],MT[n],MT[g],MT[g+1]) then s:=false;
if s then Save(MT);
end;
End;
Procedure Recurs_Soed(MT:Mass);
Var v:word;
Begin
For v:=1 to n-1 do Rekurs(MT,n-1,v)
End;
Procedure Proseivanie(var f1,f2:text);
Var st1,st2,st3:string[n];
S:boolean;
i,j,v:byte;
Begin v:=1;
Read(f1,st1);
Writeln(f2,st1);
While not eof(f1) do
begin
Readln(f1,st1);
reset(f2);{гбвў"ЁўҐ¬ Єгаб®Є ў з"® д©"}
s:=true;
st3[n]:=st1[n];
for i:=1 to n-1 do st3[i]:=st1[n-i];
{Џа®ўҐаЄ б®ўЇ¤ҐЁҐ st1 б 㦥 §ЇЁбл¬Ё ў f2}
While not eof(f2) and s do
begin
Readln(f2,st2);
j:=0;
For i:=1 to n do
if (st2[i]=st1[i]) or (st2[i]=st3[i]) then j:=j+1;
if j=n then s:=false;
end;
if s then begin Append(f2); Writeln(f2,st1); v:=v+1 end;
end;
writeln;
writeln('---',v,'---');
End;
Var MT:mass;
k,ch:word;
Loman:text;
BEGIN
clrscr;
sch:=0;
Sozd_T(MT,n,m);
assign(number,'number.txt');
Rewrite(number);
Recurs_Soed(MT);
readln;
Close(number);
Reset(number);
assign(Loman,'Loman.txt');
Rewrite(Loman);
Proseivanie(Number,Loman);
Close(Number);
Close(Loman);
readln;
END.
§3. Верхняя оценка количества способов построения ПЗЛ
Гипотеза: Пусть через n произвольных точек плоскости проходит S прямых содержащих не менее чем по 4-ре точки из данных, тогда через эти n точек возможно провести простых замкнутых ломанных не более чем ![]() где ki– количество точек из данных точек лежащих на i прямой,
где ki– количество точек из данных точек лежащих на i прямой, ![]() .
.
Доказательство:
Ι Этап.
1) Количество способов построения ломаных ![]() .
.
2) Количество способов построения замкнутых ломанных ![]() т.к. не имеет значение какая вершина будет начальной.
т.к. не имеет значение какая вершина будет начальной.
3) Очевидно, что количество ПЗЛ будет не больше количества замкнутых ломаных. Пусть L – количество способов построения ПЗЛ через n точек, тогда ![]() .
.
ΙΙ Этап.
Дано ki– количество точек лежащих на i прямой, где ![]() .
.
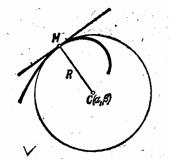
Пусть на каком-то шаге построения ПЗЛ мы пришли в т.А.
Рассмотрим рисунок.

Пусть т.АÎi-ой прямой с ki – точками из данных. Рассмотрим случаи соединения точки А с точками на i прямой.
Точку А можно соединить максимум с двумя точками, лежащих на этой прямой, чтобы выполнялись условия построения. Количество же всевозможных случаев соединения точки А с другими точками прямой равно (ki-1). Посчитаем наименьшее количество случаев, которые не удовлетворяют условиям построения.
![]()
При каждом j обращении к точкам этой прямой будут не удовлетворять ![]() случаев.
случаев.
Но т.к. таких прямых S получаем
![]()
случаев построения ломаных удовлетворяющих условиям построения.
Если не имеет значения направление обхода ломаной то, в итоге получаем количество способов построения ПЗЛ будет
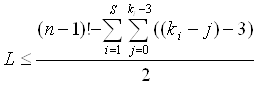
Идея: Пусть даны n произвольных точек на плоскости.
1. Выбираем любую из них, назовем "первой". Затем берем две ближайшие к ней точки. На этих трех выбранных точках строим треугольник.
2. Берем следующую ближайшую, не занятую точку к "первой".
3. Ищем ближайший отрезок
п.2 Реализация на языке Паскальuses crt,graph;
Const n=10; {Задаём количество точек}
m=400;{Длина стороны квадрата на котором расположены точки}
Type
tochka=record
x,y,r:real;
end;
Mass=array[0..n] of tochka;
Var sch:word; {Счетчик точек}
{Задает произвольным образом n точек в квадрате со стороной m }
Procedure Sozd_t(Var A:Mass; n,m:Word);
Var i:word;
Begin randomize;
For i:=1 to n do
begin
A[i].x:=random(m);
A[i].y:=random(m);
end;
End;
{Рисует отрезок ВС}
Procedure Lin(B,C:tochka);
Begin
Line(Round(B.x),Round(B.y),Round(C.x),Round(C.y))
End;
{Определяет расстояние между точками}
Function R_TT(Var A,B:tochka):real;
Begin R_TT:=Sqrt(sqr(A.x-B.x)+sqr(A.y-B.y));
End;
{Определяет расстояние между i-ой точкой и другими}
Procedure Rasst_TT(Var A:Mass; i,n:word);
Var j:word;
Begin
For j:=1 to n do
A[j].r:=R_TT(A[i],A[j])
End;
{Устраняет отрицательные значения расстояния}
Procedure absal(Var A:Mass; n1,n2:word);
Var i:word;
Begin
For i:=n1 to n2 do A[i].r:=abs(A[i].r)
End;
{Ищет номер ближайшей точки к i-ой}
Function PoiskNT(Var A:Mass; n1,n2:word):word;
var i,j:word;
Begin j:=n1;
While A[j].r<0 do j:=j+1;
For i:=n1 to n2 do
if (A[i].r>0) and (A[i].r<A[j].r) then j:=i;
PoiskNT:=j;
End;
{Сдвигает точки в массиве на 1 позицию влево начиная с n1 до n2}
Procedure Sdvyg(Var A:Mass;n1,n2:word);
Var i:word;
Begin
For i:=n1 to n2-1 do A[i]:=A[i+1];
A[n2].x:=1000; A[n2].y:=1000;
End;
{Ищет основание перпендикуляра опущенного из точки Т на прямую проходящую через точки В иС}
Procedure Osn(T,B,C:tochka;var O:tochka);
Var k,b2,a1,b1,c1:real;
Begin
If (B.x=C.x) then begin O.x:=B.x; O.y:=T.y end
else begin
k:=(B.y-C.y)/(B.x-C.x);
b2:=B.y-k*B.x;
a1:=2*(B.x-C.x)+2*k*(B.y-C.y);
b1:=2*b2*(B.y-C.y)+(sqr(C.x)-sqr(B.x))+(sqr(C.y)-sqr(B.y));
c1:=sqr(B.x-T.x)+sqr(B.y-T.y)-sqr(C.x-T.x)-sqr(C.y-T.y);
O.x:=(-c1-b1)/a1;
O.y:=k*O.x+b2;
end;
End;
{Функция истина если три точки лежат на одной прямой}
FUNCTION S_3(T,B,C:tochka):Boolean;
{Функция истина если точка Т принадлежит отрезку ВС}
Function Prin(T,B,C:tochka):boolean;
Begin
If S_3(T,B,C) then
if (((B.x<=T.x)and(T.x<=C.x)) or ((C.x<=T.x)and(T.x<=B.x))) and
(((B.y<=T.y)and(T.y<=C.y)) or ((C.y<=T.y)and(T.y<=B.y)))
then Prin:=true
else Prin:=false
else Prin:=false
End;
{Возвращает расстояние между точкой и отрезком ВС}
Function R_TO(T,B,C:tochka):real;
Var T1:tochka;
Begin
Osn(T,B,C,T1);
If prin(T1,B,C) then R_TO:=R_tt(T1,T)
else if R_tt(T,B)<=R_tt(T,C) then R_TO:=R_tt(T,B)
else R_TO:=R_tt(T,C)
End;
{Строит ломанную через точки с номера n1 до n2}
Procedure Postr(A:Mass;n1,n2:word);
Var i:word;
Begin
for i:=n1 to n2 do begin PieSlice(Round(A[i].x), Round(A[i].y), 0, 360, 2);
if i=n2 then
Line(Round(A[n2].x),Round(A[n2].y),Round(A[n1].x),Round(A[n1].y))
else Line(Round(A[i].x),Round(A[i].y),Round(A[i+1].x),Round(A[i+1].y))
end;
End;
{Выдает информацию о количестве задействованных точек}
Procedure Schet;
Var st:string;
code:integer;
Begin sch:=sch+1;
str(sch,st);
OuttextXY(600,100,st)
End;
{Истина если отрезки [AB] и [CD] имеют общие точки за исключением случаев 1) если отрезки совпадают;
2) если один конец отрезка совпадает с одним из концов другого отрезка и других общих точек нет.}
Function Peres(A,B,C,D:tochka):boolean;
Var A:mass;
B,C:tochka;
Danger,s1,s2,s3,s4:boolean;
T,OL,O,OK,OKP,i,j,t1,t2,o1,o2:word;
grDriver : Integer;
grMode : Integer;
ErrCode : Integer;
st:string;
BEGIN
sch:=0;
grDriver:=Detect;
InitGraph(grDriver, grMode, '');
ErrCode:=GraphResult;
clrScr;
Sozd_t(A,n,m); {‡¤Ґ¬ Їа®Ё§ў®"м® в®зЄЁ }
Rasst_TT(A,n);
{‘®§¤Ґ¬ ЇҐаўл© ваҐгЈ®"мЁЄ}
A[0]:=A[1];
Sdvyg(A,1,n);
A[n]:=A[0];
i:=PoiskNT(A,1,n-1);
A[0]:=A[i];{?饬 Ў"Ё¦йЁо в®зЄг Є T}
Sdvyg(A,i,n-1);
Sdvyg(A,n-1,n);
A[n]:=A[0];
i:=Poisknt(A,1,n-2);{?饬 2-о Ў"Ё¦йоо в®зЄг Є T}
{Џа®ўҐаЁ¬ "Ґ¦в "Ё ®¤®© Їаאַ©}
While S_3(A[i],A[n-1],A[n]) do {!!!!}
begin A[i].r:=-A[i].r; i:=Poisknt(A,1,n-2) end;
A[0]:=A[i];
Sdvyg(A,i,n-2);
Sdvyg(A,n-2,n);
A[n]:=A[0];
textcolor(1);
t1:=1; t2:=n-3;
o1:=n-2; o2:=n;
ClearDevice;
Postr(A,o1,o2);
readkey;
sch:=3;
Repeat
Absal(A,1,n);
{Ќе®¤Ё¬ Ў"Ё¦йЁо в®зЄг ў бв. Є®"мжҐ}
T:=Poisknt(A,t1,t2);
{‡ЇЁб뢥¬ аббв®пЁҐ ®в в®зЄЁ ¤® ®в१Є ў "Ґўл© Є®Ґж}
For i:=o1 to o2-1 do
A[i].r:=R_TO(A[T],A[i],A[i+1]);
A[o2].r:=R_TO(A[T],A[O2],A[O1]);
{?饬 г¦л© ®в१®Є}
j:=t1-1;
Repeat
{§ЇгбвЁ¬ бзҐвзЁЄ Ї®ўв®аҐЁ©}
j:=j+1;
{?饬 Ў"Ё¦йЁ© ®в१®Є}
O:=O1;
while A[O].r<0 do O:=O+1;
For i:=O1 to O2 do
if (A[i].r>0) and (A[i].r<A[O].r) then O:=i;
{[O,O+1] Ў"Ё¦йЁ© ®в१®Є}
{ЋЇаҐ¤Ґ"塞 "ЁзЁҐ Ї"®еЁе ваҐгЈ®"мЁЄ®ў}
if O=O2 then Ok:=O1 else Ok:=O+1;
Cleardevice;
setcolor(blue);
postr(A,o1,o2);
PieSlice(Round(A[o1].x), Round(A[o1].y), 0, 360, 5);
PieSlice(Round(A[o2].x), Round(A[o2].y), 0, 360, 5);
PieSlice(Round(A[t].x), Round(A[t].y), 0, 360, 3);
setcolor(15);
lin(A[t],A[o]);lin(A[t],A[ok]);
setcolor(4);
lin(A[o],A[ok]);
readkey;
s4:=false;
For i:=o1 to o2-1 do
if Peres(A[T],A[O],A[i],A[i+1]) or
Peres(A[T],A[Ok],A[i],A[i+1]) then begin s4:=true; setcolor(green); lin(A[i],A[i+1]);
str(A[i].x,st); OuttextXY(400,300,st);
str(A[i].y,st); OuttextXY(400,310,st);
str(A[i+1].x,st); OuttextXY(400,320,st);
str(A[i+1].y,st); OuttextXY(400,330,st);
str(A[T].x,st); OuttextXY(400,340,st);
str(A[T].y,st); OuttextXY(400,350,st);
str(A[O].x,st); OuttextXY(400,360,st);
str(A[O].y,st); OuttextXY(400,370,st);
str(A[Ok].x,st); OuttextXY(400,380,st);
str(A[Ok].y,st); OuttextXY(400,390,st);
readkey end;
if Peres(A[T],A[O],A[o2],A[o1]) or
Peres(A[T],A[Ok],A[o2],A[o1]) then begin s4:=true; setcolor(green); lin(A[i],A[i+1]);readkey end;
if s4 then A[O].r:=-A[O].r;
until (A[O].r>0) {or (j=t2)};
if A[O].r>0 then
Begin {ЏҐаҐ¬ҐйҐ¬ в®зЄг ’ ў ®ў®Ґ Є®"мж®}
ClearDevice;
setcolor(4);
PieSlice(Round(A[o1].x), Round(A[o1].y), 0, 360, 3);
setcolor(1);
Postr(A,o1,o2);
PieSlice(Round(A[t].x), Round(A[t].y), 0, 360, 5);
Lin(A[o],A[ok]);
delay(3000);
A[0]:=A[T];
Sdvyg(A,t,t2);
O1:=t2;
t2:=t2-1;
Sdvyg(A,O1,O); {Ћбў®Ў®¤Ё"Ё п祩Єг ¤"п ®ў®© в®зЄЁ}
A[O]:=A[0];
schet;
readkey;
End
else Danger:=true;
Cleardevice;
Postr(A,o1,o2);
Until Danger or (t2=0);
Textcolor(4);
Writeln('ђҐ§г"мвв аЎ®вл Їа®Ја¬¬л');
If Danger then begin CloseGraph; Writeln('‘®Ґ¤ҐЁвм в®зЄЁ Ґў®§¬®¦®'); readln; end
else begin ClearDevice;
Postr(A,o1,o2);
readkey;
Closegraph;
end;
END.
Список литературы
1. Фаронов Turbo Pascal 7.0.
2. Погорелов А.В. Геометрия: Учебное пособие для вузов. – 2-е изд. – М.: Наука. Главная редакция физико-математической литературы, 1984. – 288с.
3. Дискретная математика для программистов / Новиков Ф. А. – Спб.: Питер, 2001. – 304 с. :ил.
Похожие работы
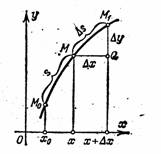
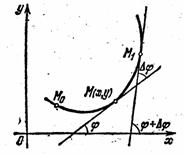
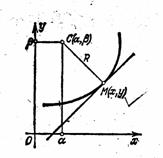
... можно показать, что формулы будут справедливы и в случае y!!<0. Параметрическое задание кривой Если кривая задана параметрически: x = j(t), y = y(t), то координаты центра кривизны можно получить из формул *, подставляя в них вместо y! и y!! их выражения через параметр: . Тогда (2) Эволюта и эвольвента Если в точке M1(x, y) данной линии кривизна отлична от нуля, то этой точке соответствует ...
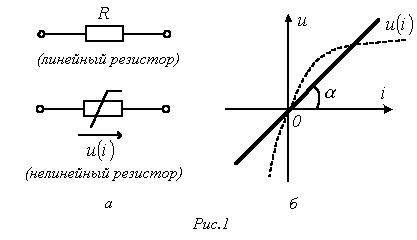
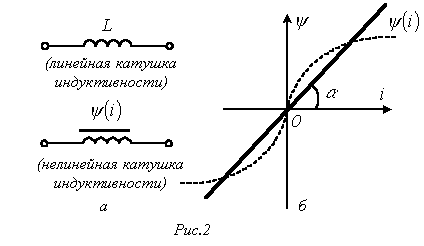
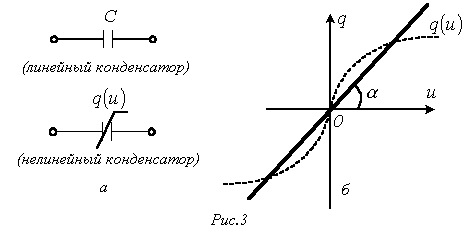
... для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5 Ответ: B= Решить задачу 5, используя соотношения (8) и (9). Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел. Переменный ток долгое время не находил практического ...
... будет подставляться вместо отсутствующих в системе шрифтов. Выберите любой шрифт, который вам нравится. ЧАСТЬ П. РАБОТА СО СТАТИЧНОЙ ГРАФИКОЙ.. Глава 4. Форматы статичной графики Итак, с пользовательским интерфейсом Macromedia Flash мы разобрались. Как выполняются типичные для всех Windows-приложений задачи, выяснили. Теперь самое время приступить к работе над графикой. Да, мы так и ...
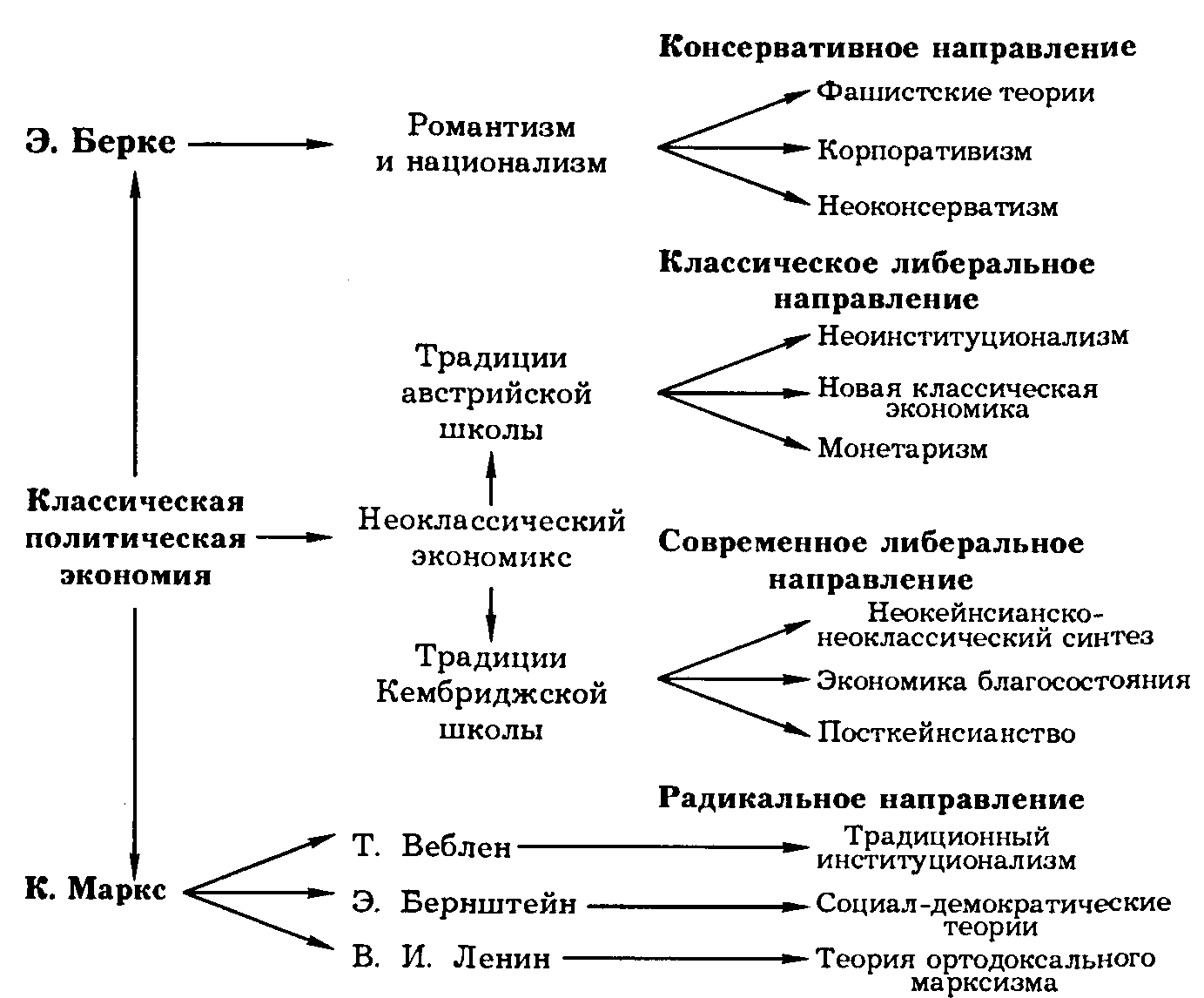
... М. В. Неоклассическая модель чистой монополии. М.: ИМЭМО, АН СССР, 1990. 3. Лейбенстайн X. Аллокативная эффективность в сравнении с "Х-эффективностью" // Теория фирмы. С. 477—506. 4. Маленво Э. Лекции... Гл. III. § 9. С. 80—85. 5. Робинсон Дж. Экономическая теория... Гл. 3—5. С. 88—130. 6. Стиглер Дж. Совершенная конкуренция: исторический ракурс // Теория фирмы. С. 299—328. 7. Самуэльсон П. ...
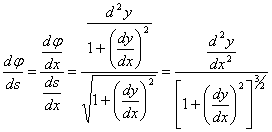
0 комментариев