Реферат по математическому анализу выполнил: студент МГТУ им. Баумана группа Э2 –11 Тимофеев Дмитрий
Москва 2004.
ВведениеДля более полного представления о кривизне плоской кривой для начала введём понятие векторной функции скалярного аргумента.
Определение 1. Если каждому значению независимого переменного tÎTÍR , называемого далее скалярным аргументом, поставить в соответствие единственный вектор r(t), то r(t) называют вектор-функцией скалярного аргумента. Вектор r(t) с началом в фиксированной точке O называют радиус-векторм.
Пусть в геометрическом (трёхмерном) пространстве задана прямоугольная декартова система координат Oxyz с ортонормированным базисом i, j, k. Тогда представление
r(t) = x(t)i + y(t)j + z(t)k
является разложением радиус-вектора r(t) в этом базисе, причем x(t), y(t), z(t) – действительные функции одного действительного переменного t с общей областью определения TÍR , называемые координатными функциями вектор-функции r(t).
Понятие кривойВведём теперь термин «кривой». Его строге определение связано с понятием вектор-функции r(t), которую будем считать непрерывной на отрезке [a, b] . Пусть в трёхмерном пространстве R3 задана прямоугольная декартова система координат Oxyz с ртонормированным базисом {i, j, k}.
Определение 2. Множество ГÌR3 точек, заданных радиус-векторм r(t) = x(t)i + y(t)j + z(t)k, tÎ[a, b] соответствующим непрерывной на отрезке [a, b] вектор-функции r(t) называют непрерывной кривой, или просто кривой, а аргумент t - параметром кривой.
При фиксированном значении t = t0 Î [a, b] параметра значения x(t0), y(t0), z(t0) являются координатами точки кривой. Поэтому одна и та же кривая может иметь как векторное так и координатное представление
Г = {r Î R3 : r = r(t), tÎ[a, b] },
Г = {(x; y; z) Î R3 : x = x(t), y = y(t), z = z(t), tÎ[a, b] }
Заданную таким образом кривую называют годографом вектор-функции r(t), поскольку именно такую кривую описывает в простарнстве конец вектора при изменении параметра t.
Кривую можно также представить как линию пересечения двух поверхностей с уравнениями F1(x, y, z) = 0, F2(x, y, z) = 0. Выбрав за параметр одну из координат, можно через него попытаться выразить из этой системы уравнений остальные координаты. Если это удастся сделать, то можно будет записать
Г = {(x; y; z) Î R3 : x = x(t), y = y(t), z = z(t), tÎ[c, d] }.
Одной и той же точке кривой могут соответствовать различные значения параметра t. Такие точки кривой называют её кратными точками. Начальной и конечной точками кривой называются точки с радиус-векторами r(a) и r(b) соответственно. Если конечная точка кривой совпадает с её начальной точкой, то кривую называют замкнутой. Замкнутую кривую, не имеющую кратных точек при tÎ(a, b) называют простым замкнутым контуром.
Определение 3. Кривую, лежащую в некоторой плоскости называют плоской.
Если эта плоскость выбрана за координатную плоскость xOy, то координатное представление плоской кривой Г имеет вид:
Г = {(x; y; z) Î R3 : x = x(t), y = y(t), z = z(t), tÎ[a, b] }.
причём равенство z=0 обычно опускают и пишут
Г = {(x; y) Î R2 : x = x(t), y = y(t), tÎ[a, b] }.
График непрерывной на отрезке [c, d] функции f(x) является плоской кривой с координатным представлением Г = {(x; y) Î R2 : x = x, y = f(x), xÎ[c, d] }.
В этом случае роль параметра выполняет аргумент x . Плоская кривая является годографом радиус-вектора r(t) = x(t)i + y(t)j или r(x) = xi + f(x)j соответсвенно.
Кривизна плоской кривой.Длина дуги иеё производная.
В введении были рассмотрены понятия векторной функции, опираясь на которое и было дано строгое определение кривой и её частного случая – плоской кривой. В данном пункте дадим определение длины дуги и найдём её дифференциал.
Пусть дуга кривой M0M (рис. 1) есть график функции y=f(x), определённой на интервале (a ,b). Определим длину дуги кривой.
Возьмём на кривой АВ точки M0, M1, M2, … , Mi-1, Mi…, Mn-1, M.
Соединив взятые точки отрезками, получим ломаную линию M0 M1M2… Mi-1 Mi…Mn-1M, вписанную в дугу M0 M. Обозначим длину этой ломаной линии через Pn.
Длиной дуги M0M называется предел (обозначим его через s), к которому стремится длина ломаной при стремлении к нулю наибольшей длин отрезков ломанной Mi-1 Mi , если этот предел существует и не зависит от выбора точек ломаной M0 M1M2… Mi-1 Mi…Mn-1M .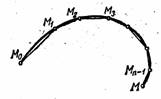
Найдём выражение дифференциала дуги.
Пусть имеется на плоскости кривая, заданная уравнением y=f(x). Пусть M0(x0, y0)- некотрая фиксированная точка кривой. Обозначим через s длину дуги M0M (рис.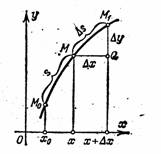 3). При изменении абсциссы x точки М длина s дуги будет меняться, т. е. s есть функция x. Найдём производную s по x.
3). При изменении абсциссы x точки М длина s дуги будет меняться, т. е. s есть функция x. Найдём производную s по x.
Дадим x приращение Dx. Тогда дуга s получит приращение Ds = дл. ÈMM1. Пусть ![]() - хорда, стягивающая эту дугу. Для того чтобы найти
- хорда, стягивающая эту дугу. Для того чтобы найти ![]() , поступим следующим
образом:
, поступим следующим
образом:
Из DMM1Q находим ![]() = (Dx)2 +(Dy)2. Умножим и разделим левую часть наDs2:
= (Dx)2 +(Dy)2. Умножим и разделим левую часть наDs2:
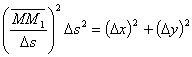
Разделим все члены равенства на Dx2:
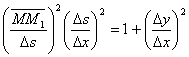
Найдём предел левой и правой частей при Dx®0. Учитывая, что ![]() и
и ![]() , получим
, получим 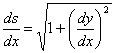
Для дифференциала дуги получим следующее выражение:
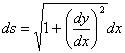 или
или ![]()
Мы получили выражение дифференциала дуги для того случая, когда кривая задана уравнением y=f(x). Но эта же формула сохраняется и в том случае, когда кривая задана параметрически:
![]()
![]()
и выражение принимает вид: ![]() .
.
Кривизна
Первая производная функции даёт нам простейшую характеристику линии y=f(x), а именно её направление. Вторая производная тесно связана с другой количественной характеристикой этой линии, с так называемой кривизной, устанавливающей меру изогнутости или искривлённости линии.
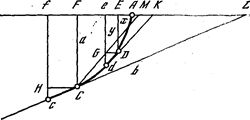
Пусть мы имеем кривую, которая не пересекает сама себя и имеет определённую касательную в каждой точке. Проведём касательные к кривой в каких-нибудь двух её точках А и В и обозначим через a угол, образованный этими касательными, или – точнее - угол поворота касательной при переходе от точки А к точке В (рис. 4). Этот угол называется углом смежности. Угол смежности в некоторой степени даёт представление о степени изогнутости дуги. У двух дуг, имеющих одинаковую длину, больше изогнута та, у которой угол смежности больше (рис. 5,4).
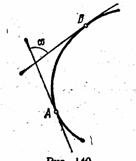 рис. 4
рис. 4 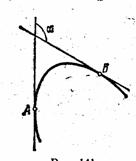 рис. 5
рис. 5
Полной характеристикой изогнутости кривой будет отношение угла смежности к длине соответствующей дуги.
Определение 4. Средней кривизной Кср дуги ÈАВ называется отношение соответствующего угла смежности a к длине дуги:
![]()
Для одной и той же кривой средняя кривизна её различных частей (дуг) может быть различной; так, например, для кривой (см. рис. 6) средняя кривизна дуги АВ не равна средней кривизне дуги А1В1 , хотя длины этих дуг равны между собой.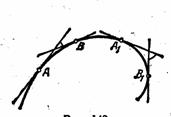
Отметим, что вблизи различных точек кривая искривлена по-разному. Для того чтобы охарактеризовать степень искривлённости данной линии в непосредственной близости к данной точке А, введём понятие кривизны в данной точке.
Определение5. Кривизной Ка линии в данной точке А называется предел средней кривизны дуги АВ, когда длина этой дуги стремится к нулю:
![]()
Выведем формулу для вычисления кривизны данной линии в любой её точке M(x, y). При этом будем предполагать, что кривая задана в декартовой системе координат уравнением вида y=f(x) и что функция имеет непрерывную вторую производную.
Проведём касательные к кривой в точках M и M1 с абсциссами x и x+Dx и обозначим через j и j+Dj углы наклона этих касательных (рис.7).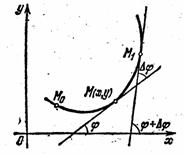
Длину дуги ÈM0M отсчитываемую от некоторой постоянной точки M0, обозначим через s; тогда Ds = ÈM0M1 - ÈM0M, а½Ds½ = ÈMM1. Как видно из (рис. 7), угол смежности, соответствующий дуге ÈMM1 равен абсолютной величине разности углов j и j+Dj, то есть равен ½Dj½.
Согласно определению средней кривизны кривой на участке
ÈMM1 имеем 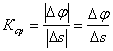 .
.
Чтобы получить кривизну в точке М, нужно найти предел полученного выражения при условии, что длина дуги ÈMM1 стремится к нулю: ![]()
Так как величины j и s зависят от x, то, следовательно, j можно рассматривать как функцию от s. Можно считать, что эта функция задана параметрически с помощью параметра x. Тогда
![]()
![]()
Для вычисления ![]() воспользуемся формулой дифференцирования функции, заданной параметрически:
воспользуемся формулой дифференцирования функции, заданной параметрически: 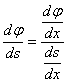 .
.
Чтобы выразить производную ![]() через функцию y=f(x), заметим,
что
через функцию y=f(x), заметим,
что ![]() и, следовательно
и, следовательно ![]() .
.
Дифференцируя по x последнее равенство, получаем 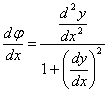 .
.
И так как 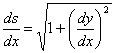 , то
, то
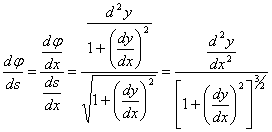 , и окончательно, так как
, и окончательно, так как ![]() , получаем
, получаем
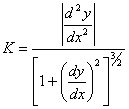 .
.
Следовательно, в любой точке кривой, где существует и непрерывна вторая производная, можно вычислить кривизну по формулам.
Вычисление кривизны линии, заданной параметрически.Пусть кривая задана параметрически: x=j(t), y=y(t). Тогда
![]()
![]()
Подставляя полученные выражения в формулу 3, получаем
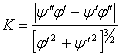 .
.
Пусть кривая задана уравнением вида r = f(q). Запишем формулы перехода от полярных координат к декартовым: x = r cos q, y = r sin q .
Если в эти формулы подставить вместо r его выражение через q, то есть f(q), то получим
x = f(q) cos q, y = f(q) sin q
Последние уравнения можно рассматривать как параметрические уравнения кривой, причём параметром является q.
Тогда![]() ,
, ![]()
![]() ,
, ![]()
Подставляя последние выражения в формулу, получаем формулу для вычисления кривизны кривой, заданной в полярных координатах:
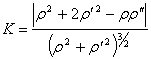
 Радиус и круг кривизны
Радиус и круг кривизны
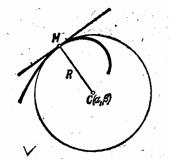
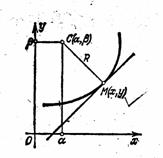
Определение 7. Величина R, обратная кривизне К линии в данной точке М, называется радиусом кривизны этой линии в рассматриваемой точке: R = 1/K, или
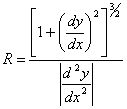
Построим в точке М нормаль к кривой (рис. 8 ), направленную в сторону вогнутости кривой, и отложим на этой нормали отрезок МС, равный радиусу R кривизны кривой в точке М.
Точка С называется центром кривизны данной кривой с центром в точке С (проходящий через точку М) называется кругом кривизны данной кривой в точке М.
Из определения круга кривизны следует, что в данной точке кривизна кривой и кривизна круга кривизны равны между собой. Выведем формулы, определяющие координаты центра кривизны.
Пусть кривая задана уравнением y=f(x). Зафиксируем на кривой точку M(x, y) и определим координаты a и b центра кривизны, соответствующего этой точке (рис. 9).Для этого напишем уравнение нормали к кривой в точке М:
![]()
Так как точка C(a, b) лежит на нормали, то её координаты должны удовлетворять уравнению ![]() .
.
Далее, точка C(a, b) находится от точки М на расстоянии, равном радиусу кривизны R:
![]()
Решив совместно уравнения * определим a, b:
![]()
![]()
![]()
![]()
и так как 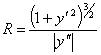 , то
, то
![]()
![]()
Чтобы решить вопрос о том, верхние или нижние знаки сле6дует брать в последних формулах, нужно рассмотреть случай y!!>0 и y!!<0. Если y!!>0 , то в этой точке кривая вогнута и, следовательно, b>y (рис. 9) и поэтому следует брать нижние знаки. Учитывая, что в этом случае ½y!!½= y!!, формулы координат центра запишем в следующем виде:
![]()
![]() (1)
(1)
Аналогично можно показать, что формулы будут справедливы и в случае y!!<0.
Параметрическое задание кривойЕсли кривая задана параметрически: x = j(t), y = y(t), то координаты центра кривизны можно получить из формул *, подставляя в них вместо y! и y!! их выражения через параметр:
![]()
![]() .
.
Тогда
![]()
![]() (2)
(2)
Если в точке M1(x, y) данной линии кривизна отлична от нуля, то этой точке соответствует вполне определённый центр кривизны C1(a, b) . Совокупность всех центров кривизны данной линии образует некоторую новую линию, называемую эволютой по отношению к первой.
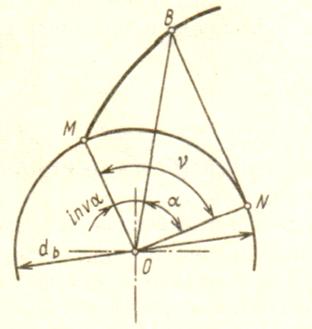
По отношению к своей эволюте данная линия называется эвольвентой или инволютой (или развёрткой). Дадим определение.
Определение 8. Геометрическое место центров кривизны линии L называется её эволютой L1 , а сама линия L относительно своей эволюты называется эвольвентой.
Если данная кривая определяется уравнением y=f(x) , то уравнения (1) можно рассматривать как параметрические уравнения эволюты с параметром x. Исключая из этих уравнений параметр x, получим непосредственную зависимость между текущими координатами эволюты a и b. Если же кривая задана параметрически x = j(t), y = y(t), то уравнеия (2) дают параметрические уравнеия эволюты.
Свойства эволютыТеорема 1. Нормаль к данной кривой является касательной к её эволюте.
Доказательство. Угловой коэффициент касательной к эволюте, определяемой параметрическими уравнениями (1) , равен 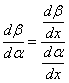 . В силу уравнений (1)
. В силу уравнений (1)
![]() , (3)
, (3)
![]() (4)
(4)
Получаем соотношение
![]() .
.
Но y! есть угловой коэффициент касательной к кривой в соответствующей точке, поэтому из полученного соотношения следует, что касательная к кривой и касательная к её эволюте в соответствующей точке взаимно перпендикулярны, то есть нормаль к кривой является касательной к эволюте.
Теорема 2. Если на некотором участке M1M2 кривой радиус кривизны изменяется монотонно, то приращение длины дуги эволюты на данном участке кривой равно по абсолютной величине соответствующему приращению радиуса кривизны данной кривой.
Доказательство.
Так как ![]() , где ds - дифференциал длины дуги эволюты; отсюда
, где ds - дифференциал длины дуги эволюты; отсюда
![]()
Подставляя сюда выражения (3) и (4) получим
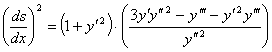 . (4)
. (4)
Так как 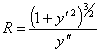 , то
, то 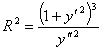 .
.
Дифференцируя по x обе части этого равенства, получим после соответствующих преобразований
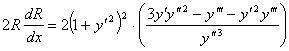
Деля обе части равенства на 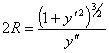 , получим
, получим
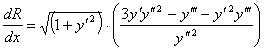 .
.
Возведём в квадрат полученное равенство:
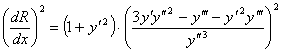 (5), и сравнивая равенства (4), (5) находим
(5), и сравнивая равенства (4), (5) находим
![]() , откуда
, откуда ![]()
По условию ![]() не меняет знак (R только возрастает или только убывает), следовательно, и
не меняет знак (R только возрастает или только убывает), следовательно, и ![]() не меняет знак. Пусть для определённости
не меняет знак. Пусть для определённости ![]() , а
, а![]() . (рис. 10)
. (рис. 10) 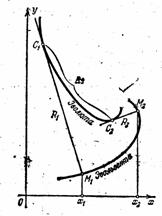 Следовательно,
Следовательно, ![]()
Пусть точка M1 имеет абсциссу x1, а M2 – абсциссу x2.
Применим теорему Коши к функциям s(x) и R(x) на отрезке [x1, x2]:
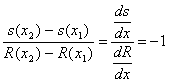
Где x - число, заключённое между x1 и x2 .
Введём обозначения (рис. ): S(x2) = s2, s(x1)= s1, R(x2)=R2, R(x1)=R1
Тогда ![]() . Но это значит, что
. Но это значит, что ![]() . Теорема доказана.
. Теорема доказана.
Доказательство при возрастании радиуса кривизны аналогично.
Если кривая задана параметрически, то теоремы 1 и 2 остаются в силе и доказываются аналогично.
Укажем без доказательства приёмы приближённых построений эволюты по эвольвенте и эвольвенты по эволюте.
1). Каждая нормаль к эвольвенте является касательной к эволюте; эволюта как бы огибает всё семейство нормалей эвольвенты. Поэтому, если постройть достаточно большое число нормалей к эвольвенте L, то огибающая их линия и будет эволютой L! (рис.11 ).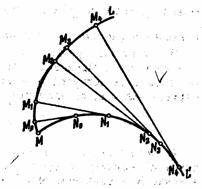
2). Если гибкую нерастяжимую нить, обтягивающую заданную выпуклую линию L! развёртывать, сохраняя постоянно натянутой, то каждая её точка опишет эвольвенту L. Поэтому эвольвенту называют ещё развёрткой. Эта операция развёртывания нити равносильна качению без скольжения прямой линии по данной линии L!; Каждая точка такой прямой описывает эвольвенту L линии L!. Отсюда следует, что данная эволюта L! имеет бесконечное число эвольвент L. В то же время любая данная линия, рассматриваемая как эвольвента, имеет только одну эволюту.
следует, что данная эволюта L! имеет бесконечное число эвольвент L. В то же время любая данная линия, рассматриваемая как эвольвента, имеет только одну эволюту.
 Заключение
Заключение
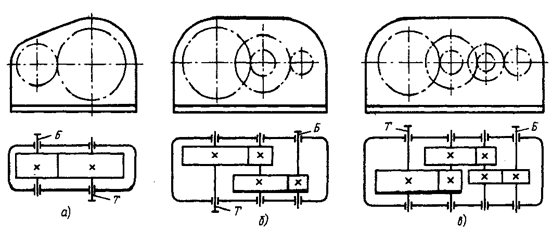
В качестве заключения рассмотрим применение эвольвенты в технике.
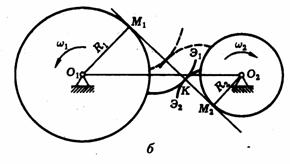
В технике эвольвенту окружности применяют для профилирования зубчатых зацеплений. Пусть боковые поверхности зубьев двух цилиндрических зубчатых колёс с параллельными осями вращения, проходящими через точки O1 и O2 (рис. б), очерчены по эвольвентам, а линия контакта зубьев при некотором взаимном положении колёс проходит через точку К. Тогда в точке К нормали КМ1 и КМ2 к эвольвентам Э1 и Э2 будут лежать на отрезке М1М2 общей касательной к окружностям радиусов R1 и R2 соответственно (эти окружности по отношению к эвольвентам являются эволютами). При вращении колёс точка К перемещается вдоль отрезка М1М2 (новое положение эвольвент показано на (рис. б) штриховыми линиями) до тех пор, пока рассматриваемая пара зубьев не выйдет из взаимного зацепления. Однако зубчатую передачу профилируют так, что к этому времени возникает зацепление между другой парой зубьев, и линия их контакта снова перемещается вдоль отрезка М1М2.
Если угловая скорость w2 ведущего колеса постоянна, то постоянна и скорость w2R2 движения точки К по линии, называемой линией зацепления. Но тогда постоянна и угловая скорость w1 =w2R2/R1 ведомого колеса. Таким образом, эвольвентное зацеплние обеспечивает плавность вращения ведомого колеса и постоянство передаточного отношения w1/w2 = R2/R1 зубчатой передачи. Кроме того, некоторые изменения межосевого расстояния O1O2, вызванные неизбежными погрешностями при установке зубчатых колёс не влияют на передаточное отношение, если эти погрешности, конечно, не столь велики, что зубья колёс вообще не могут войти в зацепление.
Эвольвентное зацепление предложено математиком Л. Эилером.
Примеры
1. Найдём кривизну параболы y = x2 в любой её точке.
Имеем: ![]() и
и ![]() . Поэтому
. Поэтому 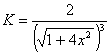 ; в частности кривизна параболы в её вершине равна 2.
; в частности кривизна параболы в её вершине равна 2.
2. Найдём кривизну прямой y = ax + b в её произвольной точке.
По формуле вычисления кривизны получаем результат К=0, означающий, что прямая представляет собой «линию нулевой кривизны».
3. Найдём уравнения эволюты параболы y = x2 .
Найдём значения X и Y: ![]() ,
, ![]()
Исключив параметр x, найдём уравнение эволюты в явном виде:
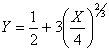
4. Определим кривизну циклоиды ![]()
![]() в её произвольной точке.
в её произвольной точке.
![]()
![]()
![]()
![]()
Подставив полученные выражения в формулу 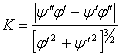 , получим:
, получим:
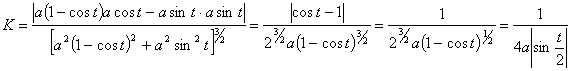 .
.
5. Найдём уравнение эволюты эллипса, заданного параметрическими уравнениями ![]()
![]()
Вычислим производные от x и y по t:
![]()
![]() Подставим данные значения в формулы
Подставим данные значения в формулы ![]() и
и ![]() :
:
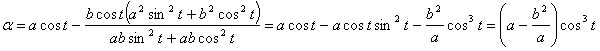
Аналогично получаем значение b: 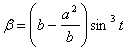 .
.
Исключая параметр t,
получаем уравнение эволюты эллипса с текущими координатами a и b в виде 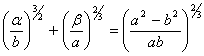 .
.
Н. С. Пискунов, Дифференциальное и интегральное исчисления, т. 1, «Наука», 1985.
А. Ф. Бермант, И. Г. Араманович, Краткий курс математического анализа, «Наука», 1966.
Е. Е. Иванова, Дифференциальное исчисление функций одного переменного, Издательство МГТУ им. Баумана, 1999.
В. А. Ильин, Э. Г. Позняк, Основы математического анализа, ч. 1, «Наука», 1982.
Б. П. Демидович, Задачи и упражнения по математическому анализу, «Интеграл – пресс», 1997.
Похожие работы
... дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности. Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например: · параболическая спираль (а - r)2 = bj, · гиперболическая спираль: r = а/j. · Жезл: r2 = a/j · si-ci-cпираль, параметрические уравнения которой имеют вид: , [si (t) и ci ...
... a2= m(z1+z2)/2= 0,3(24+49)/2= 10,95 a3= m(z1+z2)/2= 0,3(24+54)/2= 11,7 a4= m(z1+z2)/2= 0,3(24+55)/2= 11,85 a5= m(z1+z2)/2= 0,3(24+68)/2= 13,8 Определим ширину венца: b= (3…15)m= 10·0,3= 3 Определим высоту зуба: h= 2,5m= 2,5·0,3= 0,75 5. Разработка конструкций редуктора Разработка конструкции состоит в расчете и выборе его элементов: зубчатые колеса, валы, подшипники и корпуса. ...
... и доказал расходимость гармонического ряда. До сих пор в учебной литературе находит себе место парадокс И. Бернулли. Запишем таблицу 1/1*2 1/2*3 1/3*4 1/4*5... 1/2*3 1/3*4 1/4*5... 1/3*4 1/4*5... ……………………………. Просуммируем по строкам; найдем S1 = 1/1*2 + 1/2*3 + 1/3*4 + 1/4*5+...= 1 – ½ + ½ - 1/3 + 1/3 – ¼ + … = 1, S2 = ½ - 1/3 + 1/3 - ¼ +... = ...
0 комментариев