Навигация
1. Теоретическая часть
Решение задачи о поиске безусловного экстремума функции многих переменных ![]() с помощью необходимых и достаточных условий приводит к необходимости решать систему
с помощью необходимых и достаточных условий приводит к необходимости решать систему ![]() нелинейных уравнений с
нелинейных уравнений с ![]() неизвестными с последующей проверкой знакоопределенности матрицы Гессе
неизвестными с последующей проверкой знакоопределенности матрицы Гессе ![]() . Как правило, для достаточно сложных функций такая процедура решения задачи достаточно трудоемка и подразумевает численное решение нескольких задач. Поэтому возникает необходимость использовать так называемые прямые или численные методы безусловной оптимизации, которые позволяют найти стационарные точки функции, не используя аппарат необходимых и достаточных условий экстремума.
. Как правило, для достаточно сложных функций такая процедура решения задачи достаточно трудоемка и подразумевает численное решение нескольких задач. Поэтому возникает необходимость использовать так называемые прямые или численные методы безусловной оптимизации, которые позволяют найти стационарные точки функции, не используя аппарат необходимых и достаточных условий экстремума.
Компьютерный лабораторный практикум предназначен для студентов технических специальностей вузов и позволяет в наглядной и доступной форме представить численные алгоритмы отыскания экстремумов. Особенностью практикума является интерактивная форма реализации алгоритмов, при которой студент на каждой итерации принимает решение о выборе параметров методов, основываясь на числовой и графической информации о ходе процесса оптимизации.
Целью лабораторного практикума является изучение студентами прямых методов поиска безусловного экстремума двух типов функций:
· квадратичной функции 2-х переменных:
![]()
· овражной функции
![]()
Для достижения цели студент должен, изменяя параметры методов, добиться выполнения критерия окончания счета для каждого метода с одной и той же заданной точностью , из одной и той же начальной точки, за заданное для каждого метода число итераций N.
1.1 Методы, реализованные в лабораторном практикумеПрямые методы, представленные в практикуме имеют один и тот же алгоритм
![]()
где
u ![]() - текущая точка последовательности, причем
- текущая точка последовательности, причем ![]() – задается из физического содержания задачи или произвольно;
– задается из физического содержания задачи или произвольно;
u ![]() - последующая точка последовательности;
- последующая точка последовательности;
u ![]() - приемлемое направление перехода из точки в точку – направление спуска. Приемлемым при решении задачи поиска минимума функции будет только то направление, для которого
- приемлемое направление перехода из точки в точку – направление спуска. Приемлемым при решении задачи поиска минимума функции будет только то направление, для которого ![]() , что обеспечивается выполнением условия
, что обеспечивается выполнением условия ![]() ;
;
u ![]() - шаг (число >0),
- шаг (число >0),
и отличаются друг от друга способом задания ![]() и выбором
и выбором ![]() .
.
Алгоритм работы прямых методов схематически изображен на рис. 1.1
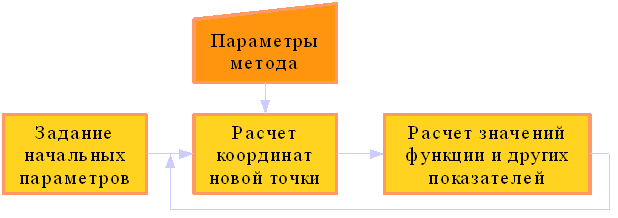
Рисунок 1.1. Алгоритм работы прямых методов
В практикуме реализованы:
l методы первого порядка, использующие информацию о 1-х производных функции ![]() :
:
· метод градиентного спуска;
· метод наискорейшего градиентного спуска;
· метод покоординатного спуска;
· метод Гаусса-Зейделя;
· метод сопряженных градиентов.
l методы второго порядка, использующие для своей реализации информацию о 1-х и 2-х производных функции ![]() :
:
· метод Ньютона;
· метод Ньютона-Рафсона;
· метод Марквардта
l Методы нулевого порядка, представленные в практикуме, позволяют производить поиск безусловного экстремума функций с помощью заданной последовательности операций. Повторение этих операций производится до тех пор, пока не будет выполнен критерий окончания, определяемый используемым методом.
В практикуме реализованы следующие методы нулевого порядка:
· метод случайного поиска
· метод деформируемого многогранника
· метод конфигураций
1.1.1 Метод градиентного спускаАлгоритм метода:
![]() ,
,
здесь:
o ![]() - направление антиградиента функции;
- направление антиградиента функции;
o ![]() - шаг выбирается из условия убывания функции в точках последовательности
- шаг выбирается из условия убывания функции в точках последовательности ![]()
Геометрическая интерпретация метода:
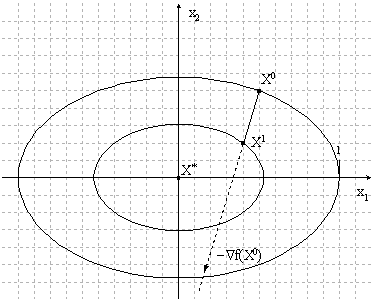
Рисунок 1.2. Геометрическая интерпретация метода
Основной критерий окончания метода:
Построение последовательности заканчивается в точке, для которой
![]()
где ![]() - заданное малое положительное число, здесь
- заданное малое положительное число, здесь

Начальные параметры метода: ![]() .
.
Изменяемый параметр метода: величина шага ![]() .
.
Особенности реализации алгоритма. Вопрос о величине шага на каждой итерации решается пользователем, причем шаг может быть, как уменьшен, если не выполняется условие ![]() , так и увеличен, если скорость сходимости алгоритма невысока (по субъективной оценке пользователя).
, так и увеличен, если скорость сходимости алгоритма невысока (по субъективной оценке пользователя).
Рекомендации по выбору параметров метода. Согласно алгоритму метода, каждая последующая точка ![]() в методе градиентного спуска ищется в направлении
в методе градиентного спуска ищется в направлении ![]() направлении антиградиента функции, построенном в текущей точке
направлении антиградиента функции, построенном в текущей точке ![]() . Поэтому, если направление антиградиента в текущей точке приблизительно совпадает с направлением на минимум (согласно чертежу), шаг следует увеличить, чтобы ускорить процесс сходимости, если же направление антиградиента сильно отличается от направления на минимум, шаг уменьшают, в противном случае функция может уменьшиться несущественно или даже возрасти.
. Поэтому, если направление антиградиента в текущей точке приблизительно совпадает с направлением на минимум (согласно чертежу), шаг следует увеличить, чтобы ускорить процесс сходимости, если же направление антиградиента сильно отличается от направления на минимум, шаг уменьшают, в противном случае функция может уменьшиться несущественно или даже возрасти.
Алгоритм метода:
![]() ,
,
здесь
· ![]() - направление антиградиента функции
- направление антиградиента функции
· ![]() - шаг вычисляется из условия наибольшего убывания функции в точках последовательности:
- шаг вычисляется из условия наибольшего убывания функции в точках последовательности:
· ![]()
Геометрическая интерпретация метода
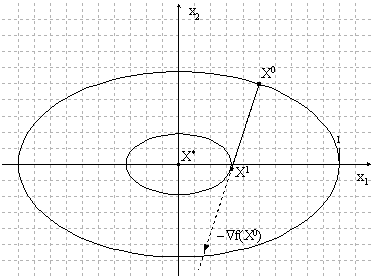
Рисунок 1.3. Геометрическая интерпретация метода
В методе наискорейшего градиентного спуска последующая точка ![]() минимизирующей последовательности также ищется в направлении
минимизирующей последовательности также ищется в направлении ![]() - направлении антиградиента функции, построенном в текущей точке, но условия вычисления шага позволяют определить наилучшее положение точки
- направлении антиградиента функции, построенном в текущей точке, но условия вычисления шага позволяют определить наилучшее положение точки ![]() на этом направлении. Как видно из чертежа, точка
на этом направлении. Как видно из чертежа, точка ![]() принимает на направлении спуска
принимает на направлении спуска ![]() предельное положение, которое характеризуется тем, что линия уровня, проходящая через точку
предельное положение, которое характеризуется тем, что линия уровня, проходящая через точку ![]() , касается направления спуска, а, следовательно, в точках минимизирующей последовательности, построенной по методу градиентного наискорейшего спуска, выполняется условие:
, касается направления спуска, а, следовательно, в точках минимизирующей последовательности, построенной по методу градиентного наискорейшего спуска, выполняется условие:
![]()
Основной критерий окончания метода:
![]()
Начальные параметры метода:
![]()
Изменяемые параметры метода: отрезок для уточнения шага ![]() .
.
Особенности реализации алгоритма. При решении задачи поиска оптимального шага ![]() , функция
, функция ![]() становится функцией одой переменной
становится функцией одой переменной ![]() , т.к.
, т.к. ![]() , а
, а
![]() и
и ![]() известны. Следовательно, задача о поиске оптимального шага
известны. Следовательно, задача о поиске оптимального шага ![]() - это задача
- это задача ![]() , которая в лабораторной работе решается численно методом дихотомии на отрезке
, которая в лабораторной работе решается численно методом дихотомии на отрезке ![]() с заданной точностью
с заданной точностью ![]() . Вопрос о границах отрезка
. Вопрос о границах отрезка ![]() на каждой итерации решается пользователем.
на каждой итерации решается пользователем.
Рекомендации по выбору параметров метода. При задании на каждой итерации отрезка ![]() для уточнения шага, следует помнить, что искомое решение может лежать как внутри, так и на границе интервала
для уточнения шага, следует помнить, что искомое решение может лежать как внутри, так и на границе интервала ![]() .
.
Проиллюстрируем ситуацию, при которой шаг ![]() вычисляется численно методом дихотомии. Для этого построим график функции
вычисляется численно методом дихотомии. Для этого построим график функции ![]() , которая в случае если
, которая в случае если ![]() является квадратичной функцией, имеет вид:
является квадратичной функцией, имеет вид:
![]()
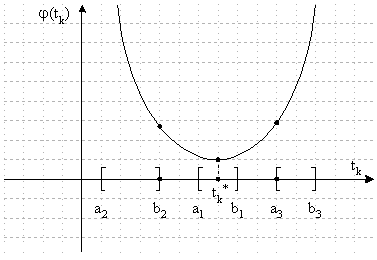
Рисунок 1.4 Метод дихотомии
Для вычислений по методу дихотомии должен быть задан отрезок для уточнения оптимального значения шага.
Как видно из чертежа, если в качестве отрезка будет выбран ![]() , оптимальное значение шага, при котором функция
, оптимальное значение шага, при котором функция ![]() принимает минимальное значение, окажется внутри отрезка, и метод с заданной точностью
принимает минимальное значение, окажется внутри отрезка, и метод с заданной точностью ![]() отыщет это значение. Если же отрезок будет
отыщет это значение. Если же отрезок будет ![]() , в качестве результата счета по методу дихотомии будет получено значение
, в качестве результата счета по методу дихотомии будет получено значение ![]() - как дающее наименьшее значение функции
- как дающее наименьшее значение функции ![]() на отрезке, аналогично при выборе отрезка
на отрезке, аналогично при выборе отрезка ![]() будет получено значение
будет получено значение ![]() .
.
Таким образом, отрезок для уточнения оптимального шага должен быть достаточно большим, чтобы гарантировано включать искомое значение шага. Признаками неверного задания отрезка ![]() являются: отсутствие касания траектории спуска из точки
являются: отсутствие касания траектории спуска из точки ![]() и линии уровня функции через точку
и линии уровня функции через точку ![]() , а также равенство величины оптимального шага величине одной из границ отрезка
, а также равенство величины оптимального шага величине одной из границ отрезка![]() .
.
Алгоритм метода:
![]()
здесь:
· ![]() - проекция на ось
- проекция на ось ![]() антиградиента функции
антиградиента функции
· ![]() - шаг выбирается из условия убывания функции в точках последовательности:
- шаг выбирается из условия убывания функции в точках последовательности:
![]()
Геометрическая интерпретация метода
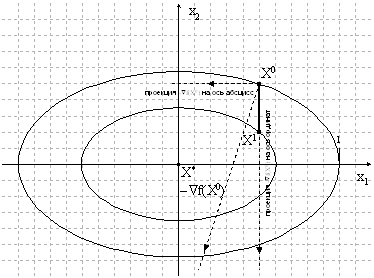
Рисунок 1.5. Геометрическая интерпретация метода
Основной критерий окончания метода: ![]()
Начальные параметры метода: ![]()
Изменяемые параметры метода: величина шага ![]() и направление проекции антиградиента (здесь абсциссы – ось
и направление проекции антиградиента (здесь абсциссы – ось ![]() , ординаты – ось
, ординаты – ось ![]() )
)
Особенности реализации алгоритма. Вопрос о величине шага на каждой итерации решается пользователем, причем шаг может быть, как уменьшен, если не выполняется условие ![]() , так и увеличен, если скорость сходимости алгоритма невысока (по субъективной оценке пользователя). Вопрос о выборе направления оси для проекции антиградиента, также решается пользователем на каждой итерации.
, так и увеличен, если скорость сходимости алгоритма невысока (по субъективной оценке пользователя). Вопрос о выборе направления оси для проекции антиградиента, также решается пользователем на каждой итерации.
Алгоритм метода:
![]()
здесь:
![]() - проекция на ось
- проекция на ось ![]() антиградиента функции
антиградиента функции
· ![]() - шаг вычисляется из условия наибольшего убывания функции в точках последовательности:
- шаг вычисляется из условия наибольшего убывания функции в точках последовательности:
![]()
Геометрическая интерпретация метода
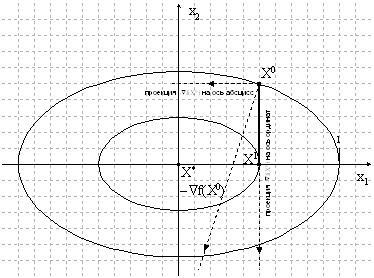
Рисунок 1.6. Геометрическая интерпретация метода
Основной критерий окончания метода: ![]()
Начальные параметры метода: ![]() .
.
Изменяемые параметры метода: отрезок для уточнения шага ![]() .
.
Особенности реализации алгоритма. Задача о поиске оптимального шага ![]() (задача
(задача ![]() ) решается численно методом дихотомии на отрезке
) решается численно методом дихотомии на отрезке ![]() с заданной точностью
с заданной точностью ![]() . Вопрос о границах отрезка
. Вопрос о границах отрезка ![]() на каждой итерации решается пользователем. Направление проекции градиента меняется циклически: сначала спуск в направлении оси абсцисс, затем – ординат и т.д.
на каждой итерации решается пользователем. Направление проекции градиента меняется циклически: сначала спуск в направлении оси абсцисс, затем – ординат и т.д.
Рекомендации по выбору параметров метода. Отрезок ![]() задается из тех же соображений, что и в методе наискорейшего спуска.
задается из тех же соображений, что и в методе наискорейшего спуска.
Алгоритм метода:
![]()
здесь:
· ![]()
· ![]()
· ![]()
· ![]() - шаг вычисляется из условия наибольшего убывания функции в точках последовательности:
- шаг вычисляется из условия наибольшего убывания функции в точках последовательности:
![]()
Геометрическая интерпретация метода
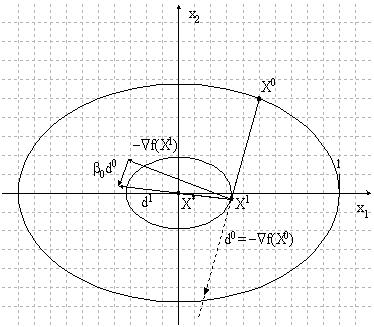
Рисунок 1.7. Геометрическая интерпретация метода
Согласно алгоритму, первая итерация метода сопряженных градиентов совпадает с первой итерацией метода наискорейшего спуска.
Вычисление величины ![]() по формуле (5.4) обеспечивает для квадратичных функций построение последовательности H-сопряженных направлений
по формуле (5.4) обеспечивает для квадратичных функций построение последовательности H-сопряженных направлений ![]() , для которых
, для которых ![]() . При этом в точках последовательности
. При этом в точках последовательности ![]() градиенты функции
градиенты функции ![]() взаимно перпендикулярны, т.е.
взаимно перпендикулярны, т.е.
![]()
Основной критерий окончания метода:
![]()
Начальные параметры метода:
![]()
Изменяемые параметры метода: отрезок для уточнения шага ![]() .
.
Особенности реализации алгоритма. Задача о поиске оптимального шага ![]() (задача
(задача ![]() ) решается численно методом дихотомии на отрезке
) решается численно методом дихотомии на отрезке ![]() с заданной точностью
с заданной точностью ![]() . Вопрос о границах отрезка
. Вопрос о границах отрезка ![]() на каждой итерации решается пользователем.
на каждой итерации решается пользователем.
Замечание. Т.к. шаг ![]() на каждой итерации вычисляется численно с точностью
на каждой итерации вычисляется численно с точностью ![]() , за счет накопления ошибки, метод сопряженных градиентов в отдельных случаях может сходиться для квадратичной функции за число итераций, превышающее число переменных.
, за счет накопления ошибки, метод сопряженных градиентов в отдельных случаях может сходиться для квадратичной функции за число итераций, превышающее число переменных.
Рекомендации по выбору параметров метода.
Отрезок ![]() задается из тех же соображений, что и в методе наискорейшего спуска.
задается из тех же соображений, что и в методе наискорейшего спуска.
Алгоритм метода:
![]()
здесь:
· ![]() - направление спуска
- направление спуска
· ![]()
Особенностью метода Ньютона является то, что при ![]() метод позволяет отыскать минимум квадратичной функции за одну итерацию.
метод позволяет отыскать минимум квадратичной функции за одну итерацию.
Геометрическая интерпретация метода для квадратичной функции:
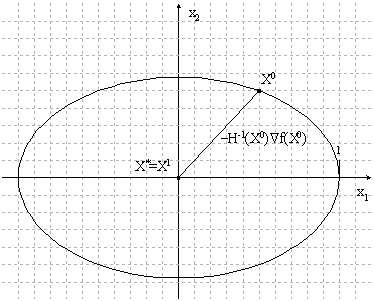
Рисунок 1.8. Геометрическая интерпретация метода
Для неквадратичной функции метод Ньютона предполагает построение последовательности минимумов аппроксимирующих квадратичных функций ![]() .
.
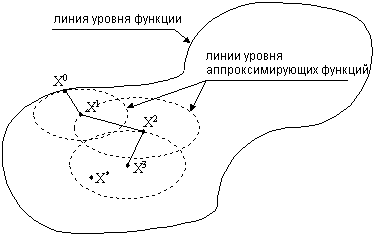
Рисунок 1.9. Последовательность минимумов
Основной критерий окончания метода: ![]()
Начальные параметры метода: ![]()
1.1.7 Метод Ньютона-Рафсона
Алгоритм метода:
![]()
здесь:
· ![]() - направление спуска
- направление спуска
· ![]() - шаг выбирается из условия убывания функции в точках последовательности:
- шаг выбирается из условия убывания функции в точках последовательности:
![]() .
.
Геометрическая интерпретация метода для квадратичной функции:
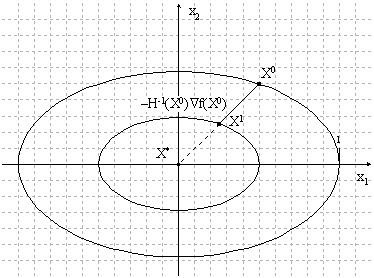
Рисунок 1.10. Геометрическая интерпретация метода
Основной критерий окончания метода: ![]()
Начальные параметры метода: ![]() .
.
Изменяемый параметр метода: величина шага ![]()
Похожие работы
... охватывало бы вопросы воспитания, взаимодействия учителей с родителями учеников и самими учениками, вопросы самоподготовки желающих учиться учеников, помощи отстающим и т.п. 5. РАЗРАБОТКА ШКОЛЬНОЙ ИНФОРМАЦИОННОЙ СИСТЕМЫ (ШИС) НА ОСНОВЕ IT-ТЕХНОЛОГИЙ ДЛЯ МОУ СОШ № 97 Поставленные в предыдущем разделе задачи могут быть решены путем организации широчайшего (относительно родителей, учеников и ...
... как философ прагматистского направления, социолог и социальный психолог. Это обстоятельство обусловило важную специфическую особенность интеракционизма: в отличие от других теоретических подходов в социальной психологии, в основе которых лежат традиционные психологические школы и направления, интеракцио-нистская ориентация пришла в социальную психологию из социологии. Понятийный аппарат и ...
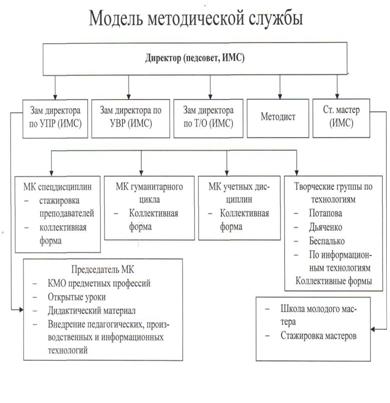
... : организации, содержания, форм проведения. При этом качественная реализация данного подхода предполагает разработку каждого из этих элементов. Глава 2. Организация методической работы на примере политехнического техникума Методическая работа может существенно влиять на качество и эффективность обучения и воспитания, на конечные результаты работы образовательного учреждения, поэтому вполне ...
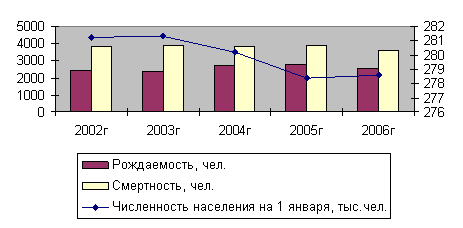
... (индикаторов) на душу населения средних значений по Приволжскому федеральному округу, по оптимистическому варианту – достижение среднероссийских показателей. 3.3. Мероприятия по совершенствованию реализации социальных услуг в сфере образования В сфере образования и воспитания необходима реализация следующих мероприятий: - расширение сети дошкольных образовательных учреждений за счет приема ...



0 комментариев