Разработка математической модели на основе описанных методов

Цель работы: Получить навыки описания метода решения математической модели на примере решения задач аналитической геометрии.

Задание: 1) Согласно заданному варианту описать методы решения задачи.

2) На основе описанных методов разработать математическую модель.

Задача: Задано множество точек, найти параметры окружности минимального радиуса, проходящие через три точки множества.

Ход работы

І)Математическая постановка задачи:

1) Найти наименьший радиус окружности по формуле: i : = 1…n

D=, где ;

j : = 1… 2)D1,D2,D3- радиусы окружности;

3) XY, XY, XY, XY- координаты точек множества;

4) D=-формула нахождения расстояния между двумя точками;

5)

-система уравнения или неравенства;

6)

-совокупность уравнения или неравенства;

7) -знак больше

-знак меньше

=-знак равно;

8) A, B, C, E- некоторые точки с определенными координатами

ІІ) Описание методов решения:

Метод 1. Метод заключается в том , что бы найти наименьший радиус окружности с помощью последовательного соединения точек с одной, а затем проделывания этого с каждой из точек множества. Затем, с помощью формулы нахождения расстояния между двумя точками

(D=),необходимо вычислить длины получившихся отрезков. После вычисления отрезки необходимо сравнить между собой. В результате если два отрезка, выходящие из одной точки, равны - это и есть радиусы окружности. Но из условия, поставленные задачей, необходимо найти минимальный радиус окружности проходящей через три точки множества. Если при сравнении несколько пар одинаковых отрезков - необходимо найти наименьшую пару – это и будет минимальный радиус окружности. (Рис.№1)

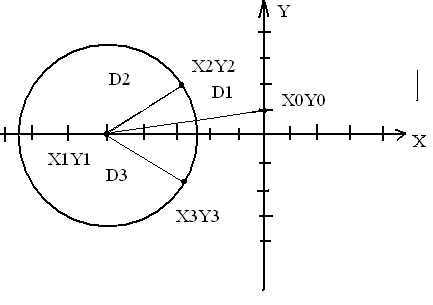
Рис.№1

Метод 2.Второй метод заключается в том, что бы искать минимальный радиус окружности при помощи соединения множество точек между собой, и в результате получение множество геометрических фигур ( в данном случае геометрические фигуры – треугольники). Затем необходимо найти расстояние сторон треугольника. Для этого возьмем формулу нахождения расстояния между двумя точками (D=). В случаи, если стороны выходящие из одной точки равны – это и есть радиусы окружности, так как через равные отрезки, выходящие из одной точки можно провести окружность с центром точки соединения этих отрезков. В случае, если в конечном результате вычисления несколько равных сторон, выходящих из одной точки, необходимо найти минимальный радиус окружности. Минимальным радиусом будут стороны с наименьшей длиной (рис.№ 2).

ІІІ) Анализ метода решения:

Первый метод более эффективен, чем второй, так как требует меньшее количество арифметических расчетов, и в памяти будет занимать меньшее количество ресурсов.

 ІY) Формализация выбранного метода:

1)         D1=

D2=

D3=;

2)         Если D1=D3, то выполняется пункт 3, иначе пункт 4;

3)         D1, D3 - радиусы окружности;

4)         Если D2=D3, то выполняется пункт 5, иначе пункт 6;

5)         D2, D3 – радиусы окружности;

6)         Если D1=D2 , то выполняется пункт 7, иначе пункт 8;

7)         D1, D2 – радиусы окружности;

8)         Если D1=D2 , и/или D2=D3, и/или D1=D3, то выполняется пункт 9;

9)         В случаи пункта 8 необходимо сравнить на меньший радиус:

D1=D2 D1=D3 D2=D3

D1D3 D1D2 D2D1

D1D3 D1D2 D2D1

D2D3 D3D2 D3D1

D2D3 D3D2D1 D3D1

10) Затем необходимо повторить это с оставшимися точками пока не перегенирируются все точки.

YІ. Геометрическое решение задачи

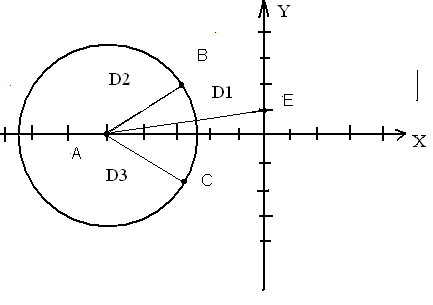
A= (-5;0);

B= (-3;2);

E= (0;1);

C= (-3;-2), так как D=, отсюда

 1) AB=

AE=

AC=

Так как AB=AC, ABAE, ACAE, значит АВ и АС- радиусы окружности с центром в точке А.

2) АВ= 

ЕВ=

СВ=

Так как АВЕВ, ЕВСВ, АВСВ, значит АВ, ЕВ, СВ- не являются радиусами окружности и точка В- не является центром окружности.

3) АЕ=

СЕ=

ВЕ=

Так как АЕСЕ, СЕВЕ, АЕВЕ, значит АЕ, СЕ, ВЕ- не являются радиусами окружности и точка Е- не является центром окружности.

4) АС=

ЕС=

СВ=

Так как АСЕС, ЕССВ, АССВ, значит АС, ЕС, СВ- не являются радиусами окружности и точка С- не является центром окружности.

Из данного множества точек можно провести только одну окружность с минимальным радиусом, проходящей через три точки множества. Отсюда следует, что минимальным радиусом являются отрезки АВ и АС.

Алгоритм реализации:

выполнять

ввод

n

пока ((n>3) и (n<20))

для i:=1..m

Вывод

‘Введите координаты’,I,’-ой точки.’

Ввод

D[i].x, D[i].y

Вывод

‘D[‘,i,’].x =’,D[i].x;

‘D[‘,i,’].y =’,D[i].y;

для i:=1..(n-3)

для k:=i+1..(n-2)

для l:=j+1..(n-1)

для j:=l+1...n

dk:= (D [i].x-D [k].x)²+(D [i].y-D [k].y)²;

dl:= (D [i].x-D [l].x)²+( D[i].y-D [l].y)² ;

dj= (D [j].x-D [j].x)²+(D [j].y-D [j].y)² ;

Если (dk=dl) или (dk=dj) тогда

Вывод

 

 

‘Точка ',i,'- является центром окружности!'

Иначе

Вывод

'Точка ',i,' не является центром окружности!'

Если (dk=dl) или (dj=dl) тогда

Вывод

' dl- возможный радиус окружности!'

Иначе

Вывод

'dl-не образует радиус..'

Если  (dk=dj) или (dk=dl) тогда

Вывод

' dk- возможный радиус окружности!'

Иначе

Вывод

'dk-не образует радиус.. '

Если  (dj=dl) или (dj=dk) тогда

Вывод

' dj- возможный радиус окружности!’

Иначе

Вывод

' dj-не образует радиус’  

если (dk<dj) и (dk=dl) то

Вывод

' dk- Наименьший радиус окружности!'

Если (dk<dl) и (dk=dj) то

Вывод

 

' dl- Наименьший радиус окружности!'

Если (dk=dj) и (dl=dk) тогда

Вывод

' dk и dj и dl- Наименьший радиус окружности!'

Листинг программы:

Program alex;

uses crt;

Type Point = Record

x,y : real;

End;

pnt = Array [1..20] Of Point;

 var

q, nstr,cstr:string;

c:char;

D:pnt;

l,n,i,k,j,code:integer;

di,dj,dk,dl,Dmin:real;

begin

clrscr;

writeln(' Донецкий государственный институт искусственного интеллекта');

writeln;

writeln;

gotoxy(40,6);

write('Кафедра програмного обеспечения');

gotoxy(40,7);

writeln(' интеллектуальных систем');

gotoxy(19,10);

writeln(' Лабораторная работа #2');

writeln(' по курсу:"Алгоритмизация вычислительных процессов"');

writeln(' тема:"Разработка алгоритмов и программы"');

gotoxy(60,20);

write('Выполнил:');

gotoxy(60,21);

write(‘');

gotoxy(60,22);

write();

writeln;

writeln;

writeln;

write('Нажмите любую клавишу');

readkey;

clrscr;

writeln(' Задание: Задано множество точек. Найти параметры окружности');

writeln('минимального радиуса проходящей через три точки множества.');

gotoxy(1,25);

write('Нажмите любую клавишу...');

readkey;

 clrscr;

 repeat

 Writeln('Введите количество точек');

 readln(nstr);

writeln;

val(nstr,n,code);

if (code<>0) then

begin

clrscr;

writeln('Это не число! Попробуйте еще раз.');

n:=5;

end;

if not( n in[3..20]) then

begin

clrscr;

code:=1;

writeln('Число не находится в заданном диапазоне! Попробуйте еще раз')

end;

until (code=0);

clrscr;

for i:=1 to n do

begin

repeat

write('Введите координату Х ',i,'-ой точки: ');

readln(cstr);

val(cstr,D[i].x,code);

if (code<>0) then

begin

writeln('Это не число! Попробуйте еще раз.');

continue

end;

clrscr;

if ((D[i].x>100) or (D[i].x<-100)) then

begin

clrscr;

writeln('Диапазон координат точек от -100 до 100!');

code:=1;

continue

end;

until (code=0);

repeat

write('Введите координату Y ',i,'-ой точки: ');

readln readln val(cstr,D[i].y,code);

if (code<>0) then

begin

clrscr;

writeln('Это не число! Попробуйте еще раз.');

code:=1;

continue

end;

clrscr;

if ((D[i].y>100) or (D[i].y<-100)) then

begin

clrscr;

writeln('Диапазон координат точек от -100 до 100!');

code:=1;

continue

end;

until (code=0);

end;

 for i:=1 to n do

 begin

 writeln('D[',i,'].x=',D[i].x);

 writeln('D[',i,'].y=',D[i].y);

 end;

for i:= 1 to (n-3) do

for k:= i+1 to (n-2) do

for l:= k+1 to (n-1) do

for j:= l+1 to n do

begin

begin

begin

begin

dk:=Sqrt(Sqr(D[i].x-D[k].x)+Sqr(D[i].y-D[k].y));

dl:=Sqrt(Sqr(D[i].x-D[l].x)+Sqr(D[i].y-D[l].y));

dj:=Sqrt(Sqr(D[i].x-D[j].x)+Sqr(D[i].y-D[j].y));

Dmin:=dk;

begin

if (dk=dl) or (dj=dl) then

writeln ('',dl:7:2,' dl-возможный радиус окружноости')

else

writeln ('dl-не образует радиус');

if (dk=dj) or (dk=dl) then

writeln ('',dk:7:2,' dk-возможный радиус окружности')

else

writeln ('dk-не образует радиус');

if (dj=dl) or (dj=dk) then

writeln ('',dj:7:2,' dj-возможный радиус окружности')

else

writeln ('dj-не образует радиус');

if (dk=dl) or (dk=dj) then

writeln ('Точка ',i,' является центром окружности')

else

writeln ('Точка ',i,' не является центром окружности!');

end;

begin

if (dk<dj) and (dk=dl) then

writeln ('dk i dl-наименьший радиус окружности') ;

if (dk<dl) and (dk=dj) then

writeln ('dk i dj-наименьший радиус окружности');

if (dk=dj) and (dk=dl) then

writeln ('dk i dj i dl-наименьший радиус окружности');

end;

end;

end;

end;

end;

readLn;

end.

Экранные формы:

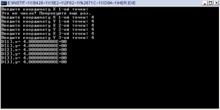
Вывод:

В ходе лабораторной работы я изучил навыки описания метода решения математической модели на примере решения задач аналитической геометрии.