Разработка программ с использованием динамической памяти

Введение

1. Постановка задачи

2. Использование динамических структур при работе с графами

2.1. Способы представления графов

2.2. Операции над графами

2.3. Описание программной реализации

2.3.1. Описание процедур и функций языка

2.3.2. Описание функций работы с динамической памятью, графами

Выводы

Приложение А Экранные формы

Приложение Б Листинг программы

1 ПОСТАНОВКА ЗАДАЧИ

Задача.

Найти все источники ориентированного графа.

Исходные данные:

- номер вершины (цел типа), вводимый пользователем;

- дуга графа, задается двумя вершинами источником и стоком, вводимая пользователем.

Промежуточные данные:

Head:TUk – указатель на голову списка смежности графа;

n,m:цел – номера вершин;

c:сим – клавиша события.

Результаты:

V:массив байт – массив вершин источников;

Ограничения:

max=10 – максимальное количество вершин;

V:массив [1..max*max].

2. Использование динамических структур при работе с графами

2.1 Способы представления графов

Способы задания графов:

-           матрица смежности;

-           матрица инцидентности;

-           список смежности;

-           список дуг (ребер);

-           и др.

Список смежности – для вершины v есть список концов дуг, исходящих из вершины v, в случае орграфа, или список смежных с v вершин, в случае неориентированного графа.

Список дуг – это список, в котом каждой дуге ставится в соответствие пара <x,y>, где x – начало дуги, а y – ее конец. Для нагруженных графов – тройка <x,y,z>,где x – начало дуги, y – конец дуги, z – вес дуги.

Матрица смежности – это квадратная матрица, строки и столбцы которой соответствуют вершинам графа. Элемент матрицы (i,j) равен 1, если вершина i связана с вершиной j ребром, иначе элемент матрицы равен 0.

Для неориентированных графов матрица смежности является симметричной относительно главной диагонали. Т.е. для получения информации о графе достаточно знать верхнюю или нижнюю треугольную матрицу смежности. Для ориентированных графов матрица смежности не является симметричной.

Матрица инцидентности – это матрица, строки которой – список вершин, а столбцы – список ребер. Элемент матрицы инциденций (i,j) равен 1, если вершина i инцидентна соответствующему ребру.

Для неориентированных графов:

Для ориентированных графов:

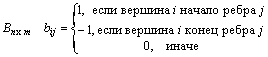
Например, дан граф G (см.рис. .1)

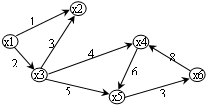
Рисунок 2.1 – Граф G

Представление графа списком смежности отображено на рисунке 2.2

Рисунок 2.2 – Список смежности графа G

Представление графа с помощью списка дуг имеет вид отображено на рисунке .3

Рисунок 2.3 – Список дуг графа G

Представление графа с помощью матрицы смежности показано в таблице 2.1

Таблица 2.1 – Матрица смежности

	x1	x2	x3	x4	x5	x6
x1	0	1	1	0	0	0
x2	0	0	0	0	0	0
x3	0	1	0	1	1	0
x4	0	0	0	0	1	0
x5	0	0	0	0	0	1
x6	0	0	0	1	0	0

Представление графа с помощью матрицы инцидентности показано в таблице 2.2

Таблица 2.2 – Матрица инцидентности

	x1x2	x1x3	x3x2	x3x4	x3x5	x4x5	x5x6	x6x4
x1	1	1	0	0	0	0	0	0
x2	-1	0	-1	0	0	0	0	0
x3	0	-1	1	1	1	0	0	0
x4	0	0	0	-1	0	1	0	-1
x5	0	0	0	0	-1	-1	1	0
x6	0	0	0	0	0	0	-1	1