Навигация
Разработка программного обеспечения для нахождения корней биквадратного уравнения
Содержание
Введение
1 Постановка задачи
2 Математические и алгоритмические основы решения задачи
3 Программная реализация решения задачи
4 Пример выполнения программы
Заключение
Список использованных источников и литературы
Введение
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. "Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37...", - поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами. Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: "Смотри!", "Делай так!", "Ты правильно нашел". В этом смысле исключением является "Арифметика" греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений. Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата – "Китаб аль-джебер валь-мукабала" ("Книга о восстановлении и противопоставлении") – со временем превратилось в хорошо знакомое всем слово "алгебра", а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений. Алгебраическое уравнение четвертой степени.
![]() ,
,
где a, b, c – некоторые действительные числа, называется биквадратным уравнением. Заменой ![]() уравнение сводится к квадратному уравнению
уравнение сводится к квадратному уравнению ![]() с последующим решением двух двучленных уравнений
с последующим решением двух двучленных уравнений ![]() и
и ![]() (
(![]() и
и ![]() - корни соответствующего квадратного уравнения).
- корни соответствующего квадратного уравнения).
Если ![]() и
и ![]() , то биквадратное уравнение имеет четыре действительных корня:
, то биквадратное уравнение имеет четыре действительных корня:
![]() ,
,
![]() .
.
Если ![]() ,
, ![]() то биквадратное уравнение имеет два действительных корня
то биквадратное уравнение имеет два действительных корня ![]() и мнимых сопряженных корня:
и мнимых сопряженных корня:
![]() .
.
Если ![]() и
и ![]() , то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:
, то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:
Случай ![]() ,
, ![]() аналогичен разобранному.
аналогичен разобранному.
![]() ,
,
![]()
Целью данной курсовой работы является разработка программного обеспечения для нахождения корней биквадратного уравнения.
1. Постановка задачи
Биквадратным называется уравнение вида ax4+bx2+c=0, где a 0. Биквадратное уравнение решается методом введения новой переменной: положив x2 = y, придем к квадратному уравнению ay2+by+c=0.
Требуется разработать программное обеспечение для нахождения корней биквадратного уравнения.
Пример 1.
Решить уравнение
x4+4x2-21=0.
Решение:
Положив x2 = y, получим квадратное уравнение y2+4y -21=0, откуда находим y1= -7, y2=3.
Теперь задача сводится к решению уравнений x2= -7, x2=3. Первое уравнение не имеет действительных корней, из второго находим
![]() ,
,
которые являются корнями заданного биквадратного уравнения..
Ответ: ![]() .
.
Пример 2.
Решить биквадратное уравнение.
2х4 – 5х2+2=0
Решение:
Обозначим х2=t. Тогда х4=(х2)2=t2 и уравнение примет вид:
2t2–5t+2=0
D=(–5)2 – 4(2)(2)=25 – 16 = 9 > 0,
t1=(5+3) / 4=2 и t2=(5 – 3) / 4=1 / 2.
Так как t=x2, то корни исходного уравнения найдем в результате решения уравнений
х1=2 и х2=1/2.
Имеем 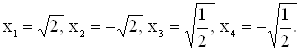
Ответ: 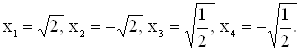
Похожие работы
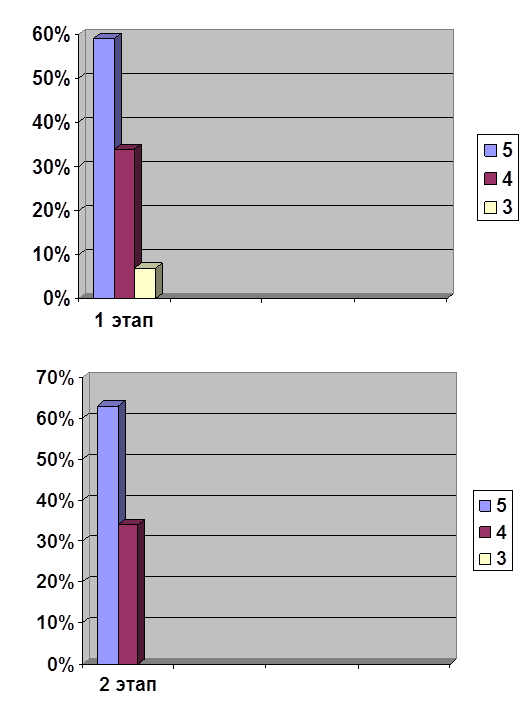
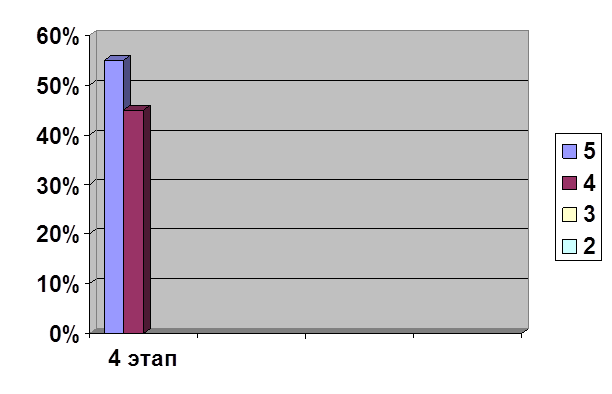
... прежнем уровне. В экспериментальном классе, котором были проведены ряд зачетных уроков, повысился уровень знаний. В ходе написания выпускной квалификационной работы по теме « Зачет как одна из форм контроля знаний учащихся по алгебре в 8 классе» были реализованы поставленные цели и задачи. Гипотеза дала положительный результат. Таким образом, разнообразие форм проверки знаний и их сочетания в ...
... заданиями, особенно, если карточка с заданием индивидуальна и ученик может работать в ней. Глава 2. Экспериментальное исследование методов и приемов систематизации и обобщения знаний учащихся при изучении темы «Алгебраические уравнения» в 9 классе 2.1. Тематическое планирование Одним из существенных моментов в организации обучения является систематизация за знаниями и умениями учащихся. ...


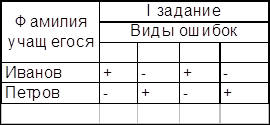
0 комментариев