Навигация
Математические и алгоритмические основы решения задачи
2. Математические и алгоритмические основы решения задачи
Рассмотрим биквадратное уравнение
ax4 + bx2 + c = 0.
Введем подстановку
y = x2.
Получим квадратное уравнение общего вида
ay2 + by + c = 0.
Таким образом, для решения биквадратного уравнения необходимо помнить, что оно свелось к системе двух уравнений второй степени:
y = x2
ay2 + by + c = 0.
Решим квадратное уравнение относительно переменной "y". Получим три возможных варианта решений:
дискриминант отрицателен: уравнение не имеет действительных решений;
дискриминант не отрицателен и равен нулю: уравнение имеет один двукратный корень;
дискриминант не отрицателен и равен нулю: уравнение имеет два различных корня.
В первом случае, когда дискриминант квадратного уравнения отрицателен, система не имеет решения, так как одно из входящих в нее уравнений, а именно квадратное уравнение ay2 + by + c = 0, не имеет решения.
Последние два случая соответствуют неотрицательному дискриминанту квадратного уравнения. Квадратное уравнение имеет действительные решения. Однако, обратите внимание на тот факт, что первое уравнение системы ax2 = y имеет смысл только при значениях y>=0. Поэтому, если оба корня квадратного уравнения ay2 +by +c = 0 отрицательны, система уравнений так же не имеет решения. Кроме того, если хотя бы один из корней квадратного уравнения ay2 +by +c = 0 отрицательный, система уравнений будет иметь только два действительных решения.
И только в том случае, когда оба корня квадратного уравнения неотрицательны, система уравнений имеет четыре действительных решения. Дадим теперь словесное описание алгоритма.
Словесное описание алгоритма решения задачи:
Ввести a, b, c.
Присвоить d = b2 - 4ac
Если d<0 перейти к 15
Присвоить y1 = (-b - SQRT(d)) / (2*a)
Присвоить y2 = (-b + SQRT(d)) / (2*a)
Если y1<0 и y2< 0 перейти к 15
Если y1<0 и y2>=0 перейти к 9
Если y1>=0 и y2<0 перейти к 13
Присвоить x1 = SQRT(y2)
Присвоить x2 = -x1
Выдать "x1=";x1, "x2=";x2
Перейти к 16
Присвоить y2 = y1
Перейти к 9
Выдать "Действительных решений нет"
Закончить
3. Программная реализация решения задачи
Файл UBikvur.h
//---------------------------------------------------------------------------
#ifndef UBikvurH
#define UBikvurH
//---------------------------------------------------------------------------
#include <Classes.hpp>
#include <Controls.hpp>
#include <StdCtrls.hpp>
#include <Forms.hpp>
#include "HandTuning.h"
#include <ExtCtrls.hpp>
#include <Menus.hpp>
//---------------------------------------------------------------------------
class TfrmBikvur : public TForm
{__published: // IDE-managed Components
THandTuning *htA;
THandTuning *htB;
THandTuning *htC;
TButton *btnCalc;
TListBox *lbxX;
TLabel *Label1;
TLabel *Label2;
TButton *btnExit;
TButton *btnClear;
TMainMenu *MainMenu1;
TMenuItem *N1;
TMenuItem *N2;
TMenuItem *N3;
TMenuItem *N4;
TMenuItem *N5;
TLabel *Label3;
TLabel *Label4;
TLabel *Label5;
void __fastcall btnCalcClick(TObject *Sender);
void __fastcall btnExitClick(TObject *Sender);
void __fastcall btnClearClick(TObject *Sender);
private: // User declarations
list<double> __fastcall Bikvur(double a, double b, double c);
public: // User declarations
__fastcall TfrmBikvur(TComponent* Owner);};
//---------------------------------------------------------------------------
extern PACKAGE TfrmBikvur *frmBikvur;
//---------------------------------------------------------------------------
#endif
Файл UBikvur.cpp
//---------------------------------------------------------------------------
#include <vcl.h>
#include <math.h>
#include <list.h>
#pragma hdrstop
#include "UBikvur.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma link "HandTuning"
#pragma resource "*.dfm"
TfrmBikvur *frmBikvur;
//---------------------------------------------------------------------------
list<double> __fastcall TfrmBikvur::Bikvur(double a, double b, double c)
{double y1, y2;
list<double> x;
//вычислене d дискриминанта
double d = b * b - 4 * a * c;
//корни существуют, если d >= 0
if(d >= 0)
{y1 = (-b - sqrt(d)) / 2 * a;
y2 = (-b + sqrt(d)) / 2 * a;}
if(d < 0 || (y1 < 0 && y2 < 0))
{Application->MessageBoxA(L"Действительных корней нет", L"Информация", MB_OK + MB_ICONINFORMATION);
return x;}
//вычисление корней биквадратного уравнения
else
{if(y1 >= 0 && y2 >= 0)
{x.push_back(sqrt(y1));
x.push_back(-sqrt(y1));
x.push_back(sqrt(y2));
x.push_back(-sqrt(y2));}
else
{if(y1 < 0 && y2 >= 0)
{x.push_back(sqrt(y2));
x.push_back(-sqrt(y2));}
else
{x.push_back(sqrt(y1));
x.push_back(-sqrt(y1));}}}
return x;}
//---------------------------------------------------------------------------
__fastcall TfrmBikvur::TfrmBikvur(TComponent* Owner)
: TForm(Owner)
{}
//---------------------------------------------------------------------------
void __fastcall TfrmBikvur::btnCalcClick(TObject *Sender)
{lbxX->Clear();
list<double> res = Bikvur(htA->Value, htB->Value, htC->Value);
int i = 1;
while(!res.empty())
{lbxX->Items->Add("x" + IntToStr(i) + " = " + FormatFloat("0.000", res.front()));
res.pop_front();
i++;}}
//---------------------------------------------------------------------------
void __fastcall TfrmBikvur::btnExitClick(TObject *Sender)
{this->Close();}
//---------------------------------------------------------------------------
void __fastcall TfrmBikvur::btnClearClick(TObject *Sender)
{htA->Value = 0;
htB->Value = 0;
htC->Value = 0;
lbxX->Clear();}
//---------------------------------------------------------------------------
4. Пример выполнения программы
Пример 1.
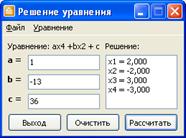
Рисунок 1 – Решение биквадратного уравнения ![]()
Пример 2.
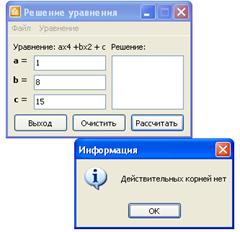
Рисунок 2 – Решение биквадратного уравнения ![]()
Пример 3.
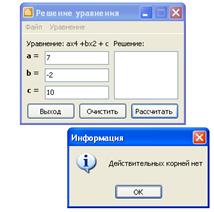
Рисунок 3 – Решение биквадратного уравнения ![]()
Пример 4.
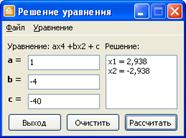
Рисунок 4 – Решение биквадратного уравнения ![]()
Пример 5.
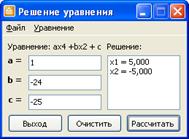
Рисунок 5– Решение биквадратного уравнения ![]()
Пример 6.
Рисунок 6 – Очистка из пункта меню
Пример 7.
Рисунок 7 – Выход из программы
Заключение
В рамках данной курсовой работы была поставлена задача: построить алгоритм и реализовать программный продукт для нахождения корней биквадратного уравнения.
В результате проектирования был составлен принципиальный алгоритм для решения поставленной задачи. Далее он был детализован и реализован на ЭВМ. В конце, был проведён анализ полученных результатов, и сделаны необходимые выводы.
Программный продукт был реализован в среде визуального программирования CodeGear RadStudio 2009 под ОС типа Windows для IBM PC-совместимых компьютеров.
Созданный программный продукт позволяет решить поставленную задачу. Также можно указать о том, что программа имеет интуитивно понятный интерфейс, что дополнительно помогает пользователю с наибольшей результативностью использовать программу.
В заключение после анализа полученных результатов были сделаны выводы, согласно которым алгоритм работает и применим для поставленной задачи.
Список использованных источников и литературы
1. Архангельский, А.Я. Программирование в С++ Builder 6. [Текст] / А.Я.Архангельский. – М.: Бином, 2003. С. 1154.
2. Ахо, А.. Построение и анализ вычислительных алгоритмов [Электронный ресурс] / А. Ахо, Дж. Хопкрофт, Дж.. Ульман. – М.: Мир. 1999. С. 143.
3. Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] / И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 2007. – 708 с.
4. Кремер, Н.Ш. Высшая математика для экономистов: учебник для студентов вузов. [Текст] / Н.Ш.Кремер, 3-е издание – М.:ЮНИТИ-ДАНА, 2006. C. 412.
5. Калиткин, Н.Н. Численные методы. [Электронный ресурс] / Н.Н. Калиткин. – М.: Питер, 2001. С. 504.
6. Биквадратные уравнения [Электронный ресурс] – Режим доступа: http://fio.ifmo.ru/archive/group34/c4wu2/pege3-2.htm
7. Павловская, Т.А. Программирование на языке высокого уровня. [Текст] / Т.А. Павловская. – М.: Питер, 2003. С. 461.
8. Семакин, И.Г. Основы программирования. [Текст] / И.Г.Семакин, А.П.Шестаков. – М.: Мир, 2006. C. 346.
Похожие работы
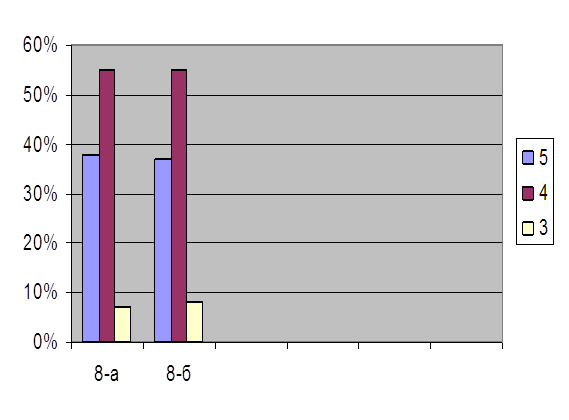
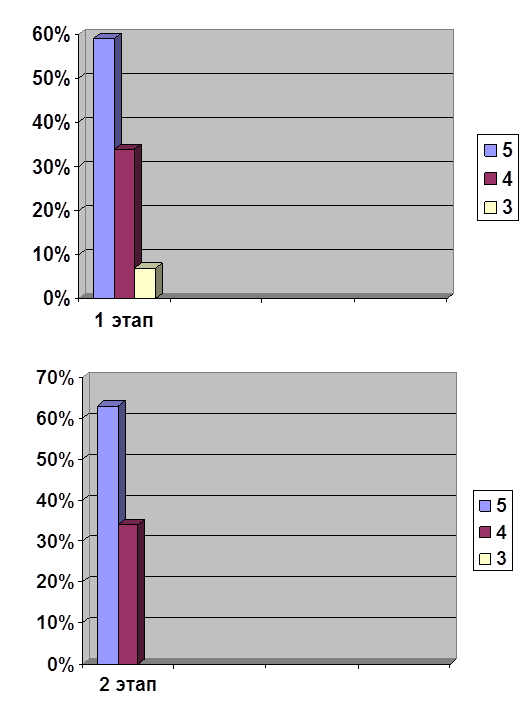
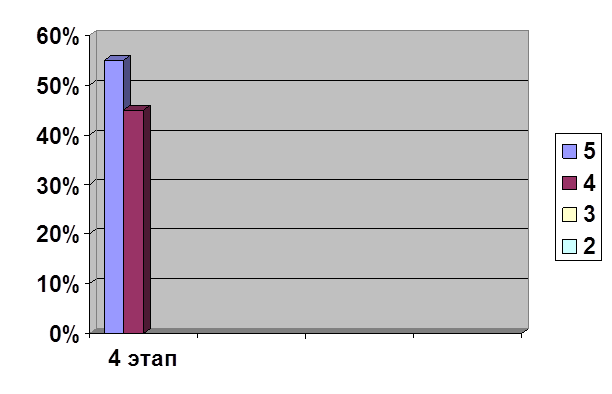
... прежнем уровне. В экспериментальном классе, котором были проведены ряд зачетных уроков, повысился уровень знаний. В ходе написания выпускной квалификационной работы по теме « Зачет как одна из форм контроля знаний учащихся по алгебре в 8 классе» были реализованы поставленные цели и задачи. Гипотеза дала положительный результат. Таким образом, разнообразие форм проверки знаний и их сочетания в ...
... заданиями, особенно, если карточка с заданием индивидуальна и ученик может работать в ней. Глава 2. Экспериментальное исследование методов и приемов систематизации и обобщения знаний учащихся при изучении темы «Алгебраические уравнения» в 9 классе 2.1. Тематическое планирование Одним из существенных моментов в организации обучения является систематизация за знаниями и умениями учащихся. ...


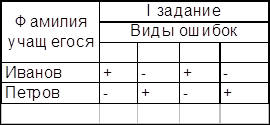
0 комментариев