Навигация
5.6.2 Выходные данные
x1: real – значение корня уравнения;
st: string – текстовые сообщения, возникающие в процессе выполнения программы (ошибки и варианты дальнейшего продолжения).
5.6.3 Промежуточные данные
Bool_of: Boolean – определяет цикл выполнения алгоритма решения;
mass: real – массив [1. . 20] ;
number: byte – глобальная переменная, номер функции;
code_of: byte – переменная, отвечающая за необходимость поиска корня уравнения;
root: real – разность приближений.
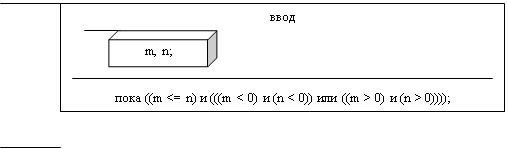
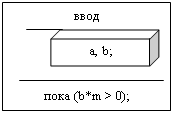
5.7. Алгоритм решения задачи 5.7.1. Алгоритм нахождения корня уравнения y(x) =a×ln(b×x)Алгоритм решения уравнения вида y(x) =a×ln(b×x) приводится на рисунке 5.4.
выполнять
 выполнять
выполнять
если (a = 0) то
 вывод
вывод
number: =0;
иначе
выполнять
i: =1; если (a*ln(b*m) *(-a/sqr(m))) > 0 то
mass [i]: =m;
code_of: =1;
иначе
Рисунок 5.4 – Алгоритм решения уравнения вида y(x) =a×ln(b×x)

если (a*ln(b*n) *(-a/sqr(n))) > 0 то
mass [i]: =n;
code_of: =1;
иначе
вывод
number: =0; code_of: =0;
если (code_of = 1) то
выполнять
x1: =mass [i] -a*ln(b*mass [i]) /
(a/mass [i]);
root: =Abs (x1-mass [i]);
i: =i+1;
mass [i]: =x1;
пока (root < E);
если (x1 < m) или (x1 > n) то
вывод
number: =0; code_of: =0;
вывод
Рисунок 5.4 – Алгоритм решения уравнения вида y(x) =a×ln(b×x) (продолжение)
5.7.2. Алгоритм нахождения корня уравнения y(x) =a×x2+b×x+c
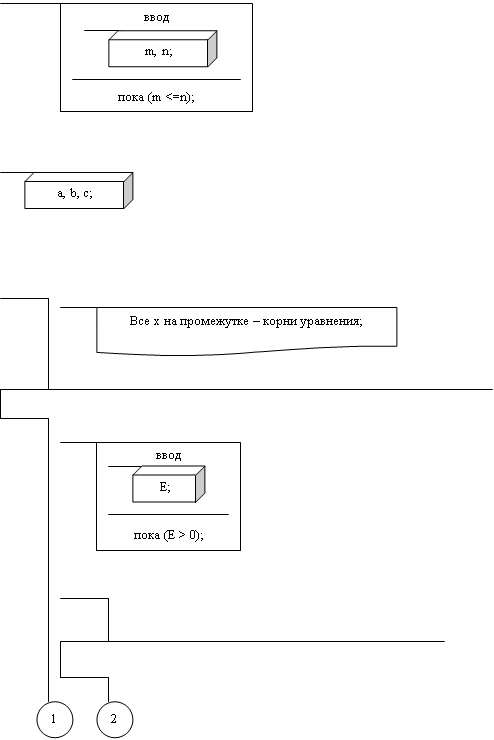
Алгоритм решения уравнения вида y(x) =a×x2+b×x+c приводится на рисунке 5.5.
выполнять
ввод
если (a = 0) и (b = 0) и (c = 0) то
вывод
number: =0;
иначе
выполнять
i: =1;
если (a*sqr(m) +b*m+c) *(2*a) >= 0 то
mass [i]: =m;
code_of: =1;
иначе
Рисунок 5.5 – Алгоритм решения уравнения вида y(x) =a×x2+b×x+c

если (a*sqr(n) +b*n+c) *(2*a) >= 0 то
mass [i]: =n;
code_of: =1;
иначе
вывод
number: =0; code_of: =0;
если (code_of = 1) то
выполнять
x1: =mass [i] -((a*sqr(mass [i]) +
b*mass [i] +c) /(2*a*mass [i] +b));
root: =Abs (x1-mass [i]);
i: =i+1;
mass [i]: =x1;
пока (root < E);
если (x1 < m) или (x1 > n) то
вывод
number: =0; code_of: =0;
вывод
Рисунок 5.5 – Алгоритм решения уравнения вида y(x) =a×x2+b×x+c (продолжение)
Алгоритмы решения уравнений рис.5.4 и рис.5.5 соответствуют procedure equation_1 и procedure equation_2 в программе соответственно.
6. КОМПЛЕКТАЦИЯ И ЗАГРУЗКА ПРОГРАММЫ 6.1. Комплектация
Папка my_stuff, в которой содержится:
– RUOP. exe – основной файл программы;
– help. asc – файл с методологической информацией;
– m_n. txt – файл, содержащий значения промежутков m и n;
– a_b_c. txt – файл, содержащий значения параметров a, b, c;
– E. txt – файл, содержащий значение погрешности E;
– egavga. bgi – файл для работы с графикой;
– keyrus. com – файл для работы с русским языком;
– trip. chr – файл, содержащий русский шрифт.
6.2. Порядок инсталляции и запуск программыТребуется скопировать папку my_stuff с содержащимися в ней файлами в папку “c: \temp\”. Для запуска программы необходимо запустить файл RUOP. exe, расположенный в папке my_stuff.
При копировании программы в иную папку, невозможными становятся работа "Справки" загрузка и автоматическое сохранение информации в файлы.
7. ТЕСТОВЫЕ ПРИМЕРЫ
Тестовые примеры необходимы пользователю для того, чтобы узнать возможности, которые предоставляет данный программный продукт или протестировать его на правильность решения уравнений.
Тестовые примеры для решения уравнения вида y(x) =a*ln(b*x) приводятся в таблице 6.1.
Таблица 7.1. Тестовые примеры для уравнения вида y(x) =a*ln(b*x)
| m | n | a | b | E | Результат |
| 1 | 10 | 1 | 0.5 | 0.01 | 2 |
| -20 | -0.01 | 9 | -2 | 0.01 | -0.2 |
| 9 | 14 | 100 | 1 | 0.01 | Уравнение не имеет корней |
Тестовые примеры для решения уравнения вида y(x) =a*x^2+b*x+c приводятся в таблице 6.2.
Таблица 7.2. Тестовые примеры для уравнения вида y(x) =a*x^2+b*x+c
| m | n | a | b | c | E | Результат |
| -10 | 10 | 5 | 29 | 3 | 0.01 | -0.1054 |
| -10 | 10 | 0 | 4 | 10 | 0.01 | -2.5 |
| 5 | 20 | 5 | 29 | 4 | 0.01 | Уравнение не имеет |
При введении в программу данных, не отвечающих требованиям типу, будет появляться сообщение "Ошибка ввода", пока не будут введены правильные данные, соответствующие требованиям программы.
Если уравнение не имеет корней, то построение графика и сохранение данных, результатов становиться невозможным.
При введении в программу данных, отвечающих требованиям, будут появляться сопроводительные сообщения (советы) по дальнейшим вариантам продолжения.
Если уравнение имеет корень, то построение графика и сохранение данных, результатов становится возможным.
ВЫВОДЫ
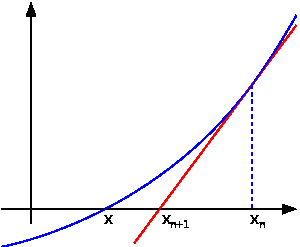
В процессе создания была написана программа, осуществляющая решение уравнения с одной переменной методом Ньютона (касательных). Программа способна решать два вида уравнений, а также выстраивать график по вводимым данным.
В программе реализована работа с графикой и с файлами, имеет интуитивно понятный интерфейс, реализована возможность справки.
Корректная работа программы обеспечивается строгим следованием методическим указаниям, а также надёжной системой проверки промежуточных результатов в ходе выполнения самой программы.
Однако ощутимыми недостатками являются расчёт результатов всего для двух функций и отсутствие касательных к графику при построении графика функции, устранение которых планируется в ближайшее время.
В целом получившийся программный продукт является отличным пособием для студентов высших учебных заведений и для учащихся математических классов среднеобразовательных школ.
ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Похожие работы
... luc – программа используется для разложения матрицы на треугольные сомножители; rluc – программа, которая отвечает за решение системы уравнений. 4. Разработка адаптивной системы управления режимами электропотребления 4.1 Функции автоматизированной системы Сбор, накопление и передача информации, характеризующей режим электропотребления комбината (информация о нагрузках). Сбор, накопление ...
... переключения с акустического анализа на прочностной. ProCAST(UES, CALCOM) Согласно исследованиям , проведенными экспертами NASA, ProCAST признана наиболее мощной и корректной программой для расчета литейных процессов. ProCAST позволяет инженеру-проектировщику рассчитывать и визуализировать в трехмерной постановке процесс течения и отверждения металла в форме, предсказывать микроструктуру, ...
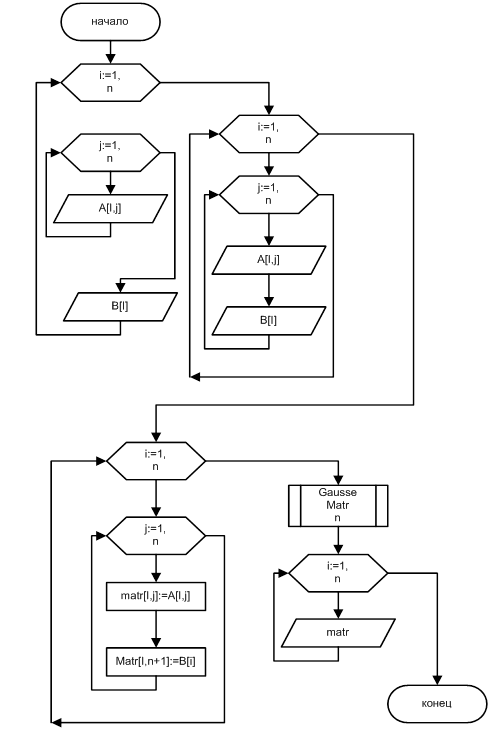
... «коды программ» стали более эффективными. В-четвертых: был улучшен интерфейс пользователя. Кроме того, в ТП 7.0 расширены возможности объектно-ориентированного программирования (в частности, расширены и улучшены возможности Turbo Vision). 8 Разработка программы решения системы уравнения методом Гаусса при помощи Turbo Pascal program Gauss; const N=3; A:array[1..N,1..N] of real = ((9.1, ...
... представлений терминологического характера, являющихся исходной базой при изучении сложных систем управления различной природы. Целью данного курсового проекта является разработка системы для оценки перспективности производственных направлений на предприятии. Для достижения поставленной цели следует разработать ряд взаимосвязанных программных модулей, а именно: - модуль подготовки данных; - ...

0 комментариев