Навигация
1.4 Код Рида – Соломона
Код Рида-Соломона позволяет скорректировать одну ошибку в одном блоке данных. При его использовании к каждому блоку информации прибавляются дополнительные два элемента X и Y, значение которых находятся исходя из условий:
для трёх единиц информации (байт):байт1 + байт2 + байт3 + X + Y = 0
байт1 + 2 * байт2 + 3 * байт3 + 4 * X + 5 * Y = 0
для расчета конкретных значений X и Y для кодирования трёх байт:
Y = 3 * байт1 + 2 * байт2 + байт3X = -4 * байт1 - 3 * байт2 - 2 * байт3
Теперь для выяснения ошибки и её коррекции применяем следующие расчеты:
Значение_ошибки = байт1 + байт2 + байт3 + X + Y
Так как ранее (до возникновения ошибки) эта сумма была равна 0, то теперь она равна непосредственно значению ошибки, которое достаточно просто вычесть из недоброкачественного байта. В случае если блок принят безошибочно, то Значение_ошибки = 0. Теперь найдём байт который надо исправлять:
N = байт1 + 2 * байт2 + 3 * байт3 + 4 * X + 5 * Y
Номер_ ошибочного_ байта = N / Значение_ ошибки
При реализации этого в реальный алгоритм необходимо обязательно осуществлять проверку на то существует ошибка в блоке или нет, то есть Значение_ошибки = 0 или нет, иначе получаем деление на ноль.
Если необходимо защитить кодом Рида-Соломона блок данных более 3х байт, то формулы расчета корректирующих значений лишь немного изменяются (для 16 байт):
Y = 16 * байт1 + 15 * байт2 + 14 * байт3 + ... + байт16X = -17 * байт1 - 16 * *байт2 - 15 * байт3 - ... - 2 * байт16
Значение_ошибки = байт1 + байт2 + байт3 + ... + X + YN = байт1 + 2 * *байт2 + 3 * байт3 + ... + 16 * байт16 + 17 * X + 18 * Y
Данным кодом неудобно защищать блоки информации менее 4 байт, так как длинна контрольных параметров X и Y должна быть как минимум 4 байта
2 байта (DW) для X и 2 байта на Y, то есть получается. что к блоку данных из 4 байт будет добавлен корректирующий блок из 4 байт.
Но что делать, если возникло две или более ошибок в блоке ?
Как один из признаков возникновения двух ошибок можно считать получения в качестве номер ошибочного байта дробного числа, например если в блоке из нулей встретится 2 единицы (две ошибки), в третьем и четвёртом байтах, то Номер ошибочного байта = 3.5 но если 4 единицы, соответственно в 3, 4 и 5 байтах то Номер ошибочного байта = 4.
2 Разработка стенда контроля передаваемой информации
Для визуализации процесса помехоустойчивого кодирования можно разработать устройство, которое поможет понять принцип работы метода Хэмминга. Кодер – декодер будем разрабатывать на основе ИМС К555ВЖ1.
2.1 Разработка устройства кодирования информации методом Хемминга
Кодер, преобразует 32х битное слово в 38ми разрядный код Хэмминга, после чего слово хранится в памяти или передаётся по шинам и т.д. В процессе передачи или хранения в слове может произойти ошибка, поэтому декодер не просто декодирует слово, но и исправляет единичные ошибки. Процесс кодирования и декодирования можно представить в виде блок-схемы приведенной ниже.
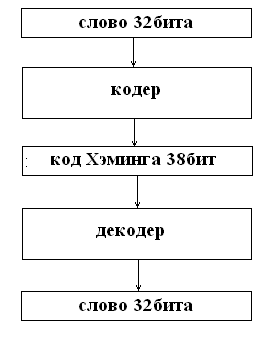
Рис. 2.1 блок схема кодирования
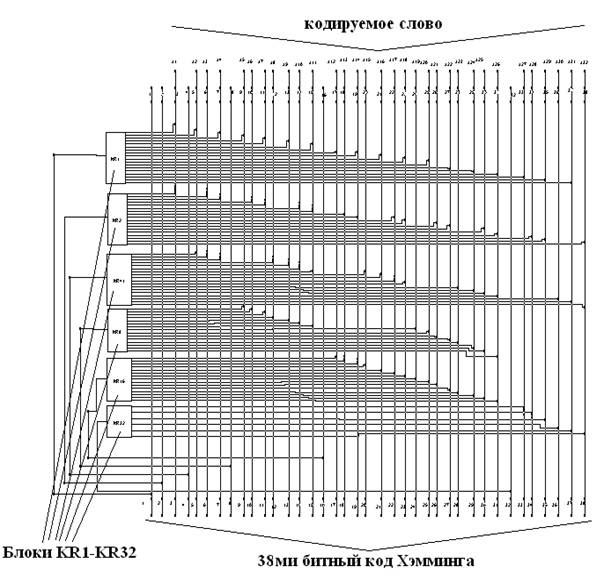
Рис. 2.2 — Схема кодера
На входы а1,а2…а32 подаётся кодируемое слово. Блоки (элементы) KR1, KR2, KR4, KR8, KR16 и KR32 формируют контрольные разряды (биты чётности). Весь процесс кодирования сводится к формированию контрольных разрядов и сдвигу имеющихся разрядов. Так, 1й бит слова становится 3м битом кода, а 2й – 5м , 1,2,4,8,16,32 биты – контрольные. В результате кодирования 32х битное слово становится 38ми битным.
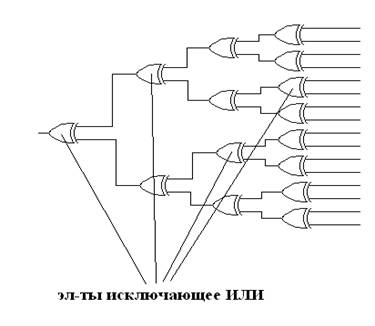
Рис 2.3 — Схема блоков KR1 – KR32
Блоки KR1, KR2, KR4, KR8, KR16 и KR32 собраны элементах исключающее ИЛИ. Итак:
Блок KR1 формирует 1й контрольный разряд подсчитывая чётность 3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35 и 37 битов, если количество единиц в этих разрядах чётное, то контрольный бит равен нулю, если нечётное – единица.
Аналогично блок KR2 формирует 2й контрольный разряд, подсчитывая чётность 3,6,7,10,11,14,15,18,19,22,23,26,27,30,31,34,35 и 38 битов, если количество единиц в этих разрядах чётное, то контрольный бит равен нулю, если нечётное – единица.
Блок KR4 формирует 4й контрольный бит проверяя 5,6,7,12,13,14,15,20,21,22,23,28,29,30,31,36,37 и 38 биты.
Блок KR8 формирует 8й контрольный бит проверяя 9,10,11,12,13,14,15,24,25,26,27,28,29,30 и 31 биты.
Блок KR16 формирует 16й контрольный бит проверяя 17,18,19,20,21,22,23,24,25,26,27,28,29,30 и 31 биты.
Блок KR32 формирует 32й контрольный бит проверяя 33,34,35,36,37 и 38 биты.
2.2 Разработка устройства декодирования информации методом Хемминга
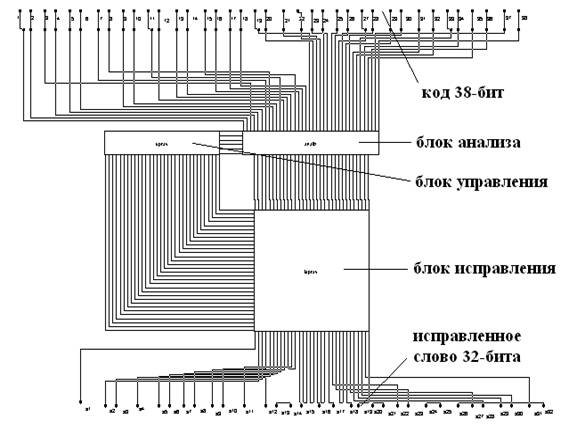
Рис.2.4 — Схема декодера
Схема декодера состоит из 3х основных блоков: блока анализа, блока управления и блока исправления. Декодер осуществляет декодирование с исправлением произошедшей ошибки.

Рис. 2.5 — Схема блока анализа
Блок анализа с помощью блоков KR1, KR2, KR4, KR8, KR16 и KR32 заново проверяет чётность выше упомянутых разрядов и с помощью 6 и элементов исключающее ИЛИ сравнивает с пришедшими по шине контрольными разрядами. Если контрольные разряды нарушены, то формируются 6 сигналов ошибки, которые передаются в блок управления. Так же блок анализа изымает из 38ми битного слова биты чётности и передаёт 32х битное слово в блок исправления.
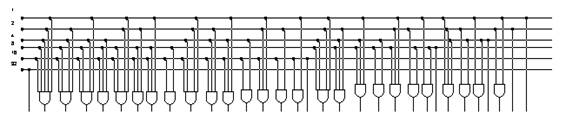
Рис. 2.6 — Схема блока управления
Блок управления представляет дешифратор 6/32, собранный на базе элементов И. В соответствии с комбинацией входных сигналов, блок управления активирует тот или иной управляемый инвертор блока исправления.
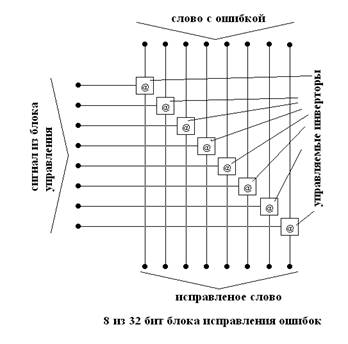
Рис 2.7 — Схема блока исправления ошибок
Блок исправления непосредственно производит исправление слова пришедшего из блока анализа в соответствии с сигналами блока управления. Он представляет собой 32 управляемых инвертора, на информационные входы которых подаётся слово с ошибкой, а на управляющие код из блока управления. В соответствии с поданным сигналом активируется тот или иной инвертор, который и исправляет ошибку, и слово выводится из дешифратора.
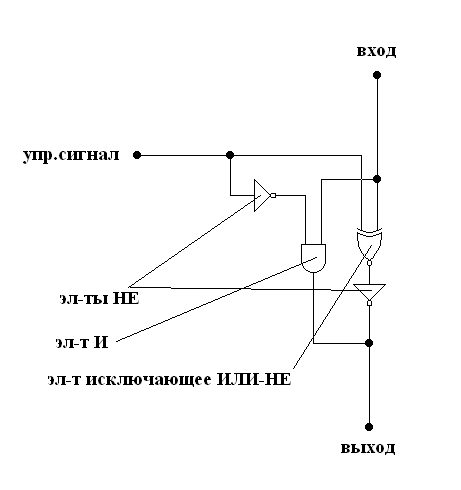
Рис.2.8 — Схема управляемого инвертора
Управляемый инвертор собран на базе 2х элементов НЕ, элемента И, и элемента исключающее ИЛИ-НЕ. Является непосредственно исполнителем исправления ошибки. Его таблица истинности приведена ниже.
Табл. 2.1 — таблица истинности управляемого инвертора
| ВХОД | УПР.СИГНАЛ | ВЫХОД |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Похожие работы
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
... за которым следует устройство дискретизации (рисунок 4.2), подастся известный сигнал s(t) плюс шум AWGN n(t). 4.4 Межсимвольная интерференция На рисунке 4.3 а) представлены фильтрующие элементы типичной системы цифровой связи. В системе - передатчике, приемнике и канале - используется множество разнообразных фильтров (и реактивных элементов, таких как емкость и индуктивность). В передатчике ...
... ? 8. Какими программами можно воспользоваться для устранения проблем и ошибок, обнаруженных программой Sandra? Раздел 3. Автономная и комплексная проверка функционирования и диагностика СВТ, АПС и АПК Некоторые из достаточно интеллектуальных средств вычислительной техники, такие как принтеры, плоттеры, могут иметь режимы автономного тестировании. Так, автономный тест принтера запускается без ...
... и сеть Internet. АПЗ.38.098424.003 ПЗ Изм Лит № докум Подпись Дата МНОГОФУНКЦИОНАЛЬНЫЙ КОНТРОЛЛЕР ВЗУ Пояснительная записка Лит Лист Листов Разраб Борщ С. К 2 20 Провер Скороделов В. ...
0 комментариев