Навигация
Обзор существующих решений
4 Обзор существующих решений
4.1 Алгоритм сокращения критического пути (CPR)
CPR предложен разными авторами из голландского политехнического университета Delft и французского института INRIA. Сначала алгоритм был разработан для планировщика задач в многопроцессорных системах, где граф задач можно моделировать в виде ориентированного ациклического графа. Существуют и другие подходы для решения такого рода задач (TwoL, CPA, TSAS) [5], но CPR показывает самый приемлемый результат.
CPR можно применить для распределения многоблочных задач (при условии возможности построения ориентированного ациклического графа).
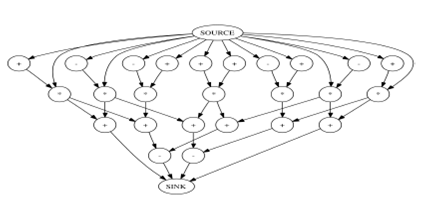
Рисунок 2. Иллюстрация ориентированного ациклического графа блоков
Определение
Критический путь (T): самый длинный путь в графе (от входа до выхода).
Верхний критический путь блока t (Tv): самый длинный путь от входа до t
Нижний критический путь блока t (Tn): самый длинный путь от t до выхода
P - количество процессоров в системе.
N(t) - Количество процессоров, выделенных для блока t.
Описание алгоритма
Шаг 1. Для каждого блока ti выделен один процессор N(ti) = 1. Построить расписание.
Шаг 2. Пусть X – множество всех блоков, для которых выделено меньше P процессоров.
Шаг 3. Пусть блок t – блок, у которого сумма Tv + Tn максимальная.
Выделить для t дополнительный процессор, N(t) = N(t) + 1. Построить новое текущее расписание.
Если после выделения, новый критический путь T’ < T то T = T’, иначе N(t) = N(t) – 1 и блок t исключить из множества X и считать предыдущее расписание текущим.
Шаг 4. Повторяем шаг 3 пока X не пусто
Суть алгоритма состоит в выделении максимально возможного количества процессоров для каждого блока с целью сокращения критического пути (т.е. сокращение общего времени выполнения всех блоков). Данный алгоритм исходит из наличия алгоритма построения расписания.
Алгоритм эффективный, учитывает зависимости между блоками, но не рассматривает проблему назначения групп процессоров для конкретных блоков и составления расписания их прохождения.
4.2 Упаковка в контейнеры
Bin-packin это множество алгоритмов для решения задачи: объекты различных объемов должны быть упакованы в конечное число контейнеров так, чтобы минимизировать количество используемых контейнеров. В нашем случае упаковка в контейнеры используется для равномерного распределения задач по всем процессорам.
Упаковка в контейнеры без разбиения объектов
Имеем список объектов L=(a1, a2, …, an) и их размеры s(ai) Є {1, 2, …, U}. Размер контейнеров V больше U, количество контейнеров m. Отсортируем список объектов по размеру в убывающем порядке. Первые m объектов упаковывать соответственно будем в m контейнеров. С остальными объектами действуем по принципу: упаковывать в контейнер, у которого занимаемого места меньше всего.
Упаковка в контейнеры с разбиением объектов
Существует два возможных варианта упаковки в контейнеры с разбиением объектов [4]: с сохранением и с увеличением объема данных. Будем рассматривать вариант с увеличением объема данных, так как после разбиения часто появляются дополнительные коммуникации между фрагментами.
Имеем список объектов L=(a1, a2, …, an) и их размеры s(ai) Є {1, 2, …, U}, U – размер контейнеров.
Введем некоторые понятия:
· Эффективность алгоритма A: RA(L) = A(L)/OPT(L), где A(L) – нужное количество контейнеров когда применяем алгоритм A на список объектов L, OPT(L) – оптимальное количество контейнеров для данного списка объектов.
· R называется асимптотической эффективностью в худшем случае, если
R = inf{r>=1: для некоторых N>0, RA(L)<=r для всех L где OPT(L)>=N}
· Алгоритм А называется алгоритмом без лишнего разбиения если:
a) Разбивает объект только тогда, когда его размер больше размера контейнера
б) Разбивает объект на два фрагмента так, чтобы первый фрагмент вместится полностью в одном из контейнеров
в) Открывает новый контейнер только тогда, когда в уже открытых контейнерах нельзя упаковать новый фрагмент.
Известно, что для всех алгоритмов упаковки в контейнеры без лишнего разбиения:
R <= U/(U-2), U>2
Теперь рассмотрим алгоритмы NF, NFD, NFI, FFD-I
· NF - Next-Fit
На каждом шаге открываем только один контейнер, упаковываем объекты по очереди, если размер объекта больше размера свободной части контейнера – разобьем на две части так, чтобы первая часть заполнила контейнер. После этого открываем новый контейнер и вторую часть туда упаковываем. Это очень простой алгоритм и имеет плохую эффективность
RNF=U/(U-2), U>=6
· NFD, NFI (Next-Fit с ранее отсортированным списком объектов по размеру в убывающем/возрастающем порядке)
RNFD >= U/(U-2) если U=2n, n>=3
RNFD >= (U+1)/(U-1) если U=2n+1, n>=2
Но это только нижняя оценка, мы вполне сможем подобрать пример, когда NFD и NFI работают тоже плохо, как и NF.
· FFD-I и FFI-I (Iterative First-Fit Decreasing/Increasing with Item fragmentation)
Попробуем упаковать все объекты списка L в фиксированное количество m контейнеров. Сортируем список объектов по размеру в невозрастающем порядке. Каждый объект будем упаковывать в первый подходящий контейнер, если такого нет, разобьем объект на две части. Первая часть должна заполнить первый свободный контейнер, а вторую часть положим в отсортированный список объектов. Если не удалось упаковать все объекты в m контейнеров, увеличиваем m и повторяем.
Пусть s(L) – сумма всех объектов в списке L.
1) Взять m=[s(L)/U]
2) FFD()
3) Если успешно, останавливаем
4) Иначе m=m+1 и goto 2)
Для алгоритма FFD-I:
RFFD-I <= U/(U-1) если U<=15
U/(U-1) < RFFD-I < U/(U-2) если U>=16
Получаем, что FFD-I лучше NFD/NFI и NF.
Алгоритм упаковки в контейнеры без разбиения показывает хорошие результаты, но не учитывает параллелизм внутри блоков (исходит из последовательной постановки). Так как алгоритм упаковки в контейнеры с разбиением исходит из идеального распараллеливания на мультикомпьютере – без обменов, то, в условиях необходимости синхронизации в процессе счета подзадачи, он не даёт ответа на вопрос составления итогового расписания, расположения объектов внутри контейнера, а также не учитывает необходимость разбиения объекта на равные части.
0 комментариев