CONTINUE

50 CONTINUE

*DVM$ END TASK_REGION

преобразовать так:

*DVM$ TASK_REGION TSA

*DVM$ PARALLEL (IB) ON TSA(renum(IB) )

DO 50 IB = 1,NBL

CALL JACOBI(block(renum(IB))%PA, block(renum(IB))%PB,SIZE(1, renum(IB)), SIZE(2, renum(IB)))

50 CONTINUE

*DVM$ END TASK_REGION)

После этих модификаций программа будет использовать функционал разработанного программного средства. Схематично процесс представлен на рисунке 5.

Рисунок 5. Схема работы разработанного программного средства

Схема на рисунке 5 отражает работу с разработанной библиотекой. Кроме этого также возможна работа в диалоговом режиме с разработанной исполняемой программой для генерации отображений. Для работы с ней, необходимо запустить исполняемый файл и следовать инструкциям, появляющимся на экране. Есть возможность сгенерировать случайным образом блоки, их характеристики; задать вручную; прочитать из файла. Формат файла, описывающего блоки таков: первая строка содержит количество процессоров, за ней построчно идут описания блоков, для каждого блока отдельная строка вида «порядковый номер время последовательной части время параллельной части минимальное количество процессоров максимальное количество процессоров». Программа построит отображение, проверит его корректность, выведет временные характеристики работы алгоритма отображения, временные характеристики полученного отображения; а также, в случае небольшого размера входных данных, выведет на экран в виде текстовой диаграммы картину загрузки процессоров. На рисунке 6 изображен пример сессии работы с разработанным программным средством в диалоговом режиме.

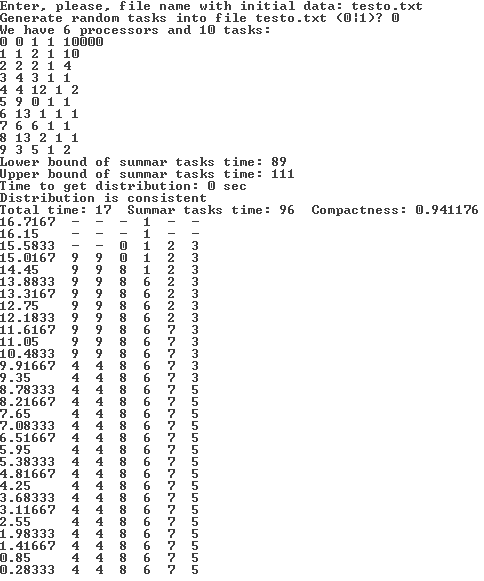
Рисунок 6. Пример сессии работы с разработанным программным средством в диалоговом режиме

6.4 Характеристики функционирования

Пусть имеется n подзадач и m процессоров, тогда алгоритмическая сложность разработанного программного средства при использовании алгоритма «Транспонированное Отображение» асимптотически не превосходит C * (n * log(n) + n * m). Затраты по памяти асимптотически не больше C * (n + m), где C равен 2 килобайтам плюс-минус 30 процентов. Время работы на тесте из 10000 блоков, 2048 процессоров на процессоре Intel Core 2 Duo 2.33 ГГц составило 100 секунд. При реализации были использованы быстрые структуры данных такие, как красно-черные деревья с помощью стандартной библиотеки шаблонов языка Си++, а само представление данных было оптимизировано под алгоритм.

Алгоритм был протестирован на данных о блоках реальной задачи из 810 подзадач по моделированию аэродинамики самолета при отображении на 29, 57, 128, 256, 384 процессоров.

Оценки времени выполнения каждой подзадачи брались по закону Амдала с долей последовательной части равной 0,1. Запусков счета этой задачи с различными отображения не производилось, все расчеты времени в условных единицах и являются теоретическими на основании знаний о размерах блоков.

Получаемые отображения сравнивались с результатами работы алгоритма отображения без учета параллелизма подзадач («Жадное Отображение»), а также с одним из вариантов используемого в DVM отображения, работающему по алгоритму:

Пусть есть M процессоров

Пусть size(i) – размер i-го блока

1.         Посчитать суммарный размер блоков, пусть он равен S

2.         Положить счетчик процессоров curProc равным единице. Положить счетчик промежуточного суммарного размера блоков curSum равным нулю.

3.         Для каждого блока i выполнять:

             Отобразить задачу i на процессор curProc.

             curSum = curSum + size(i)

             Если curSum >= curProc * S / M то curProc = curProc + 1

4.         Конец цикла

Рисунок 7. Сравнение результатов отображения различных алгоритмов на различном количестве процессоров

Как видно из диаграмм на рисунке 7, на больших количествах процессоров (начиная с 57), алгоритм с использованием параллелизма внутри подзадачи дает лучшие результаты.

Также заметно, что на 128, 256, 384 процессорах у алгоритмов, не учитывающих параллелизм подзадач, итоговое время исполнения совпадают это происходит из-за наличия нескольких подзадач сложности 11648, что заметно больше остальных сложностей. Получается, что эти наиболее сложные подзадачи тормозят выполнение других менее сложных подзадач. А в случае с 384 процессорами почти в три раза.

Также были проведены реальные тесты на кластере СКИФ-МГУ на другой многоблочной задаче – модельной задаче с 10 блоками. Были произведены запуски одной и той же задачи с использованием алгоритмов «Транспонированное Отображение» и ручного отображения, работающего по следующему алгоритму:

1. Если количество блоков меньше количества процессоров, то каждый блок отобразить на все имеющиеся процессоры

2. Если количество блоков не меньше количества процессоров, то, если n блоков и m процессоров, i-ый блок отобразить на процессоры [1 + (i-1)*(m/n) .. i * (m/n)]

Для каждого алгоритма были произведены пуски с использованием 1, 4, 9, 10, 16, 56 процессоров. В качестве результата бралось общее время работы всей задачи в секундах – в ней внутри каждого блока считался Якоби, 100 итераций. На рисунке 8 наглядно продемонстрированы полученные времена работы.

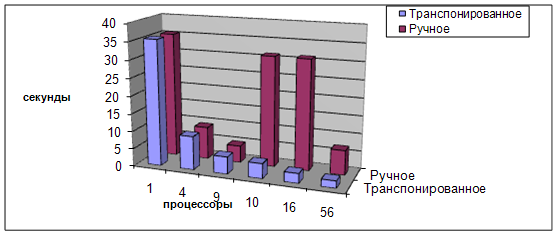
Рисунок 8. Сравнение результатов отображения различных алгоритмов на различном количестве процессоров

7 Заключение

В рамках этой работы рассмотрены разные алгоритмы для отображения многоблочных задач. Предложен эффективный алгоритм отображения подзадач, использующий возможность распараллеливания подзадач. Он реализован в составе статической библиотеки, подключаемой во время компиляции совместно с системой поддержки времени исполнения LibDVM, а также в виде интерактивного приложения для генерации отображений.

В дальнейшем стоит задача автоматического определения границ блоков (сейчас блоки определяются ручным образом) для сетки сложной структуры, а также задача усовершенствования предлагаемого алгоритма отображения вводом в рассмотрение неоднородных вычислительных систем, а также учётом затрат на коммуникации.

8 Список цитируемой литературы

1. Н.А. Коновалов, В.А. Крюков, А.А. Погребцов, Н.В. Поддерюгина, Ю.Л. Сазанов. Параллельное программирование в системе DVM. Языки Fortran DVM и C-DVM. Труды Международной конференции "Параллельные вычисления и задачи управления" (PACO’2001) Москва, 2-4 октября 2001 г., 140-154 с.

2. M. Jahed Djomehri, Rupak Biswas, Noe Lopez-Benitez. Load balancing strategies for multi-block overset grid applications [PDF] (http://www.nas.nasa.gov/News/Techreports/2003/PDF/nas-03-007.pdf)

3. Oliver Sinnen. Task Scheduling for Parallel Systems // John Wiley And Sons, Inc. 2007.

4. Nir Menakerman, Raphael Rom. Bin Packing with Item Fragmentation // Algortihms and Data Structures. Springer Berlin / Heidelberg, 2001. Volume 2125/2001. P. 313-324

5. Andrei Radulescu, Arjan J.C. van Gemund. A Low-Cost Approach towards Mixed Task and Data Parallel Scheduling // ICPP. 2001. P. 69-76

6. Buyya, Rajkumar. High Performance Cluster Computing : Architectures and Systems, Volume 1 // Prentice Hall. 1999.

7. GCC, the GNU Compiler Collection [PDF] (http://gcc.gnu.org/onlinedocs/gcc-4.5.0/gcc.pdf)