Расчет и анализ системы обслуживания робототехнического комплекса производства деталей ЭВА

2. Расчет и анализ системы обслуживания робототехнического комплекса производства деталей ЭВА

 

2.1 Расчет при бесприоритетном обслуживании

Таблица 3 - Исходные данные

i	li	ci	const
1	0,9	8	0,55
2	0,8	7
3	0,7	6
4	0,6	5

При бесприоритетном обслуживании имеем на входе суммарный пуассоновский поток с интенсивностью, которая определяется по формуле:

.(2.1.1)

Длительность обслуживания характеризуется вторым средневзвешенным моментом, который находится по формуле:

,(2.1.2)

где b_i⁽²⁾ – это дисперсия экспоненциального распределения, которая зависит от параметра распределения µ через соотношение:

.(2.1.3)

По условию, задано отношение , которое мы обозначили, как Const_, тогда:

,(2.1.4)

где b_i – математическое ожидание экспоненциального распределения.

, .

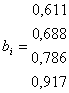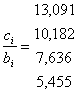.(2.1.5)

Тогда с учетом (2.1.2), (2.1.3) и (2.3.4) формул получим окончательное выражение суммарной дисперсии:

,(2.1.6)

где λ – интенсивность суммарного потока заявок в систему

,(2.1.7)

,

.

Длительность обслуживания характеризуется также средневзвешенными потерями:

,(2.1.8)

.

Тогда среднее время ожидания:

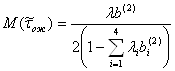,(2.1.9)

.

Суммарные потери вычисляются по формуле:

,(2.1.10)

.

 

2.2 Расчет при оптимальных относительных приоритетах

При относительных приоритетах среднее время ожидания заявок типа  равно:

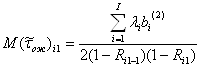,(2.2.1)

где R_i1—коэффициент загрузки системы всеми заявками от 1-го до i₁-го типа включительно.

Расчет коэффициента загрузки канала r:

,(2.2.2)

.

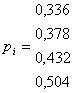Расчет коэффициента загрузки системы:

,(2.2.3)

.

С учетом выше приведенных формул выражение можно переписать в виде:

.(2.2.4)

Введя временную переменную V_remper= , получим следующее выражение:

, (2.2.5)

.

Расчет среднего времени ожидания заявок:

,

,

,

.

Суммарные потери:

.