Необходимо совершить поворот вокруг оси OZ по часовой стрелке на угол α

2. Необходимо совершить поворот вокруг оси OZ по часовой стрелке на угол α.

 .

Матрица поворота, таким образом, будет равна:

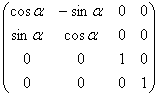
3. Необходимо совершить поворот вокруг оси OX по часовой стрелке на угол β.

.

Матрица поворота, таким образом, будет равна:

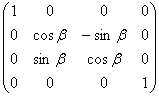
Умножив M₃ на M₂, а результат на M₁ получим искомую матрицу перехода:

2.3.4 Программная реализация

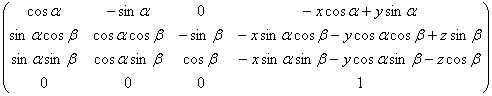
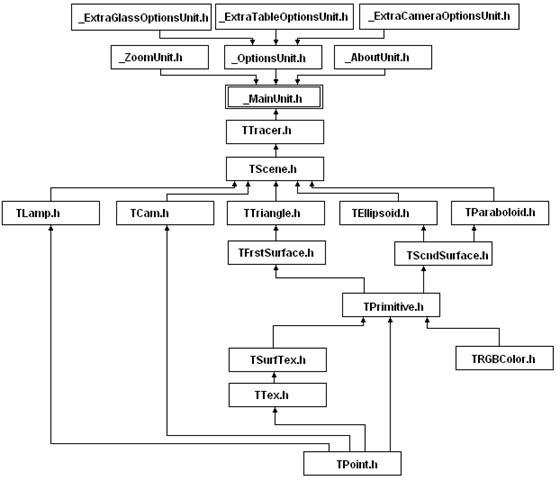
Во многих функциях и процедурах в программе в качестве входных и выходных параметров выступают матрицы. Поэтому в программе введен специальный тип:

TMatrix=Array [0. .11] of real

Это массив из 12 элементов типа real. Он представляет собой последовательно записанные три верхние строчки матрицы. Я не включил последнюю строчку, так как она одинаковая у всех матриц преобразования и равна (0, 0, 0,1).

Для операций над матрицами в программе предусмотрены следующие процедуры:

1. Procedure MatrixAB (var Res: TMatrix; const M1,M2: TMatrix)

Процедура умножает матрицу M1 на матрицу M2 и помещает результат в Res.

2. Procedure ShiftMatrix (var M: TMatrix; Z: real)

Создает матрицу перехода из текущей системы координат в систему координат, сдвинутую по оси OZ на z.

Процедура перемещает систему координат, задаваемую матрицей M, по оси OZ на z.

3. Procedure SetMatrix (var M: TMatrix; dx,dy,dz,x,y,z: real) overload

Создает матрицу перехода из текущей системы координат в систему координат, находящуюся в точке (x,y,z), ось OZ которой направлена по вектору (dx,dy,dz).

4. Procedure SetMatrix (var M: TMatrix; dx,dy,dz: real) overload

Создает матрицу перехода из текущей системы координат в систему координат, ось OZ которой направлена по вектору (dx,dy,dz).

Преобразование координат

Для преобразования координат точки из одной системы координат в другую необходимо умножить матрицу преобразования на столбец координат точки.

Для преобразования точки из одной системы координат в другую в программе существует процедура Trans (const M: TMatrix; var F: TPoint; const V: TPoint).

В V содержатся координаты точки, координаты которой надо преобразовать.

В F содержатся результат.

M - матрица преобразования.

В процедуру Ray передается только матрица перехода из глобальной системы координат в систему, связанную с лучом (M_i).

Процедура находит координаты вторичного луча в новой системе координат.

Составляет матрицу перехода из текущей системы в систему, связанную с лучом (L_i+1).

Умножает матрицы M_i+1=L_i+1M_i

Вызывает рекурсивно Ray с параметром M_i+1

 

2.3.5 Определение пересечения луча с треугольником

Преобразуем все вершины треугольника в локальную систему координат, связанную с лучом. Луч в этой системе координат имеет координаты (0, 0,1). После этого задача сводится плоской. Необходимо определить, лежит ли точка (0, 0) внутри треугольника в проекции на плоскость OXY.

Преобразуем координату x вершин треугольника в локальную систему координат.

Проверяем, лежат ли точки треугольника все справа от нуля или все слева. Если да, то пересечения с треугольником нет. Если нет, то:

Преобразуем координату у вершин треугольника в локальную систему координат.

Проверяем, лежат ли точки треугольника все сверху от нуля или все снизу. Если да, то пересечения с треугольником нет. Если нет, то:

Необходимо, чтобы при обходе треугольника по часовой стрелке точка (0,0) лежала справа от каждой стороны (либо наоборот). Это можно установить, проверив одного ли знака три векторных произведения:

, , .

Если не одного знака, то пересечения нет, Если одного, то:

Преобразуем координату z вершин треугольника в локальную систему координат.

Определяем нормаль к треугольнику, для этого умножим векторно два вектора

 и

В случае если, NZ равно нулю, луч параллелен оси OZ и соответственно лучу. Значит, пересечения нет. В другом случае пересечение есть.

Находим координаты пересечения.

Составим уравнение плоскости, в которой находится треугольник:

,

подставим x=0 и y=0,

 

2.3.4 Формирование отраженного луча

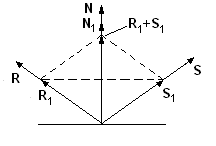
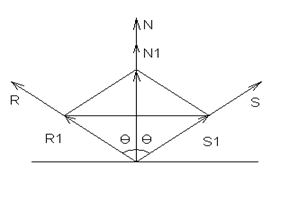
Обозначим отраженный луч через R, вектор, направленный против падающего луча - S, вектор нормали - N. Рассмотрим единичные векторы этих векторов R₁, S₁, N₁. Так как все три вектора находятся в одной плоскости, то можно записать R₁+S₁=N^’. Длина вектора N^’ равна 2cosθ. Так как векторы N^’ и N₁ сонаправленные, то можно записать:

N’=N₁2cosθ.

Таким образом

.   

Поставим условие, что падающий и отраженный лучи имеют одинаковую длину.

Так как падающий луч в локальной системе координат имеет координаты (0, 0,1). То вектор S будет иметь координаты (0, 0, - 1). Подставим его координаты в выражение для отраженного луча. Получим

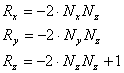
2.3.5 Формирование преломленного луча

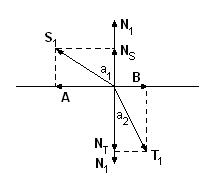
Обозначим преломленный луч, имеющий единичную длину, через T₁. Единичный вектор нормали - через N₁. А вектор, направленный противоположно падающему лучу - через S₁. Разложим вектор S₁ на A и N_s, а вектор T₁ на B и N_T. Вектор равен

.

Найдем вектор N_T. Этот вектор противоположен по направлению вектору нормали, а длина его равна

.

Таким образом

.

Для того, что бы определить cosα₂, запишем закон преломления

.

Воспользуемся тождеством

Получим

Значение для cosα₁ можно выразить через скалярное произведение единичных векторов S₁ и N₁. С учетом этого можно записать выражение для вектора

N_T:

Найдем вектор B. Он располагается на одной прямой с вектором A, причем

 .

Найдем отношение длин векторов A и B:

. Отсюда

.

Если подкоренное выражение отрицательно, то это соответствует полному внутреннему отражению. В этом случае преломленный луч создаваться не будет. Учтем то, что вектор S равен (0, 0,1).

2.4 Оболочки

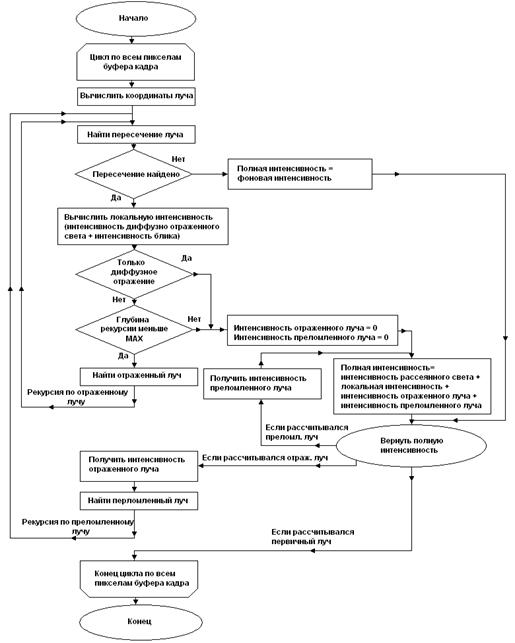
В алгоритме трассировки лучей от 70 до 90 процентов временных затрат занимает процедура определения пересечений луча с объектами сцены. Если перебирать все объекты сцены, то время будет пропорционально Cn, где С - количество пикселей, а n - число объектов на сцене. Улучшить алгоритм можно, если каким-нибудь образом попробовать сократить число перебираемых объектов. Очень простой, но эффективной является идея иерархических оболочек. Предположим, что нам надо изобразить содержимое полки с посудой. Проведем мысленно большую сферу вокруг полки, так чтобы она включала и полку, и посуду на ней. Затем сферу вокруг каждого предмета посуды. Теперь представим себе процесс рендеринга. Проверяем, пересекается ли луч с самой большой сферой. Если нет, то это значит, что луч не пересекает внутренние оболочки, переходим к другому лучу. Если пересекает, то смотрим пересечение луча с подсферами данной сферы. Как видно из такого примера, многие лучи могут совершить всего одну проверку и отсеяться.

При построении оболочек необходимо, чтобы главная оболочка целиком включала все ее подоболочки, иначе не будет работать правило: "Если луч не пересекает главную оболочку, то он не пересекает и все ее подоболочки". Так же при построении оболочек желательно, чтобы оболочки, имеющие один порядок вложенности, пересекались по как можно меньшему объему. Это улучшит эффективность алгоритма. Метод оболочек помогает сделать время рендеринга пропорциональным Clog (n).

2.4.1 Алгоритм построения иерархических оболочек

Для начала строятся сферические оболочки вокруг всех треугольников сцены. Этим занимается процедура Obol1. Сферы выбираются таким образом, чтобы все точки треугольника лежали внутри сферы. Для построения оболочки вокруг треугольника процедура:

Находит минимальный параллелепипед, в котором находится весь треугольник.

Определяет середину параллелепипеда.

Находит расстояния от центра до каждой вершины треугольника, определяет максимальное среди них. Оно и будет являться радиусом нашей оболочки. А центром будет центр параллелепипеда.

Далее вызывается процедура Obol2. Она и занимается собственно построением иерархии. Процедура создает одну оболочку, в которую записывает номера всех треугольников, сцены и вызывает рекурсивную процедуру step с параметром 1. Это значит, что step обработает первую оболочку.

Процедура step:

Определяет центр и радиус сферы, которая включает в себя все треугольники данной оболочки.

Перемещаем мысленно систему координат в центр этой сферы. Создаем 8 оболочек, каждая оболочка отвечает за свой октант в перенесенной системе координат.

Распределяем треугольники рассматриваемой сферы, по этим 8 оболочкам (октантам) по принципу: если центр сферы вокруг треугольника лежит в октанте, то треугольник помещается в соответствующую оболочку.

Если какая-то оболочка оказалась пуста (т.е. если в нее не попал не один треугольник), то она уничтожается.

Устанавливается связь: в запись оболочки добавляются номера ее подоболочек.

Так же, в текущую оболочку записываем номера треугольников, радиус оболочки которых больше четверти радиуса текущей оболочки. Эти треугольники не должны заноситься ни в одну из подоболочек. В процессе обхода оболочек они должны обрабатываться отдельно.

Рекурсивно вызываем процедуру Step для каждой из оболочек. Процесс будет продолжаться до тех пор, пока в каждой получившейся оболочке не будет один треугольник, либо пока очередное разбиение не изменит ситуацию (в результирующей оболочке останется столько же треугольников, сколько в исходной).

То, что большие треугольники рассматриваются отдельно, дает выигрыш во времени, так как при этом оболочки, мало перекрываются. Данное соотношение размеров было подобрано экспериментально. При нем достигается наибольший выигрыш по времени.

 

2.4.2 Алгоритм обхода оболочек в трассировке лучей

Устанавливаем текущей первую оболочку.

Для трассируемого луча проверяется, пересекается ли он с текущей оболочкой. Если нет, то выводим цвет фона. Если да, то идем на п.3.

Пересекаем луч с большими треугольниками данной оболочки.

Если у оболочки нет подоболочек, то ищем пересечения с треугольниками этой оболочки. Если же у нее есть подоболочки, то вызываем п.2 для них всех.

При пересечении оболочек с лучом необходимо преобразовать, центры оболочек в систему координат, связанную с лучом.

При повороте или сдвиге всех объектов сцены, необходимо преобразовывать и центры оболочек. Если же совершаются преобразования не над всей сценой, а только над отдельными объектами, то необходимо произвести полный перерасчет оболочек.

2.5 Текстурирование

 

2.5.1. Процедуры для работы с текстурами

Для работы с текстурой предусмотрены 3 функции:

1. AddTeksture

Эта функция загружает текстуру в память. Входным данным для нее является имя файла, в котором находится текстура. Для успешной загрузки текстуры необходимо, чтобы она:

имела размеры, равные степени двойки

была в формате BMP

имела глубину цвета равную 24.

Функция возвратит true при успешной загрузке текстуры и false при неудаче.