Навигация
1 при i - нечетном;
Ci =
1 при i - чётном;
4. С автоматическим выбором шага
Точность вычисления определенного интеграла зависит от величины шага интегрирования. Ошибка в выборе величины шага интегрирования либо не обеспечит нужной точности, либо приведет к необоснованным затратам машинного времени.
Заданную точность при рациональных затратах времени на вычисления обеспечивают алгоритмы интегрирования с автоматическим выбором шага. Идея метода автоматического выбора шага интегрирования для достижения заданной точности заключается в следующем:
а) выбирается начальное n и вычисляется шаг h= (b-a) /n;
б) рассчитывается значение интеграла I1 для этого шага h;
в) шаг h уменьшается в два раза, т.е. h=h/2 и вычисляется значение интеграла I2;
г) оценивается погрешность между двумя значениями r=½I1-I2½; если погрешность r меньше или равна заданной точности, т.е. r<=e, то точность достигнута и значение интеграла I=I2; если r>e, то точность не достигнута и величине I1 присваивается более точное значение I2;
д) теперь повторяются этапы в) и г) до выполнения условия r<=e.
Вычисление определенного интеграла с помощью пакета MathCAD в нормальном и символьном виде.
Для решения интеграла численно и в символьном виде необходимо задать функцию f (x) и найти от неё интеграл  на промежутке [a, b].
на промежутке [a, b].
Для вычисления численного значения заданного интеграла:
С помощью встроенных функций задаём определённый интеграл;
После нажатия клавиши "=", MathCAD выдаёт значение интеграла на заданном промежутке.
В Mathcad:
![]()
При решении интеграла в символьном виде:
С помощью встроенных функций задаём интеграл;
Вызов в меню "Математика" подменю "Булен" и нажатие "®" или Control+. приводит к вычислению интеграла в символьном виде.
В Mathcad:
![]()

В Turbo Pascal:
Текст программы вычисления
определенного интеграла методом
средних прямоугольников на TP
program Sredniipriamougolniki;
uses crt;
var a,b,h,s,y,x: real;
i,n: integer;
begin clrscr;
write ('Vvedite a,b,n=');
readln (a,b,n);
h: = (b-a) /n;
x: =a+h/2;
s: =0;
for i: =1 to n do
begin
s: =s+1/sqr (3*sin (x) +2*cos (x));
x: =x+h;
end;
y: =h*s;
writeln ('n=',n,' y=',y: 10: 3);
readkey;
end.
Результаты работы программы:
a=0 b=1 n=1000 y=0.117
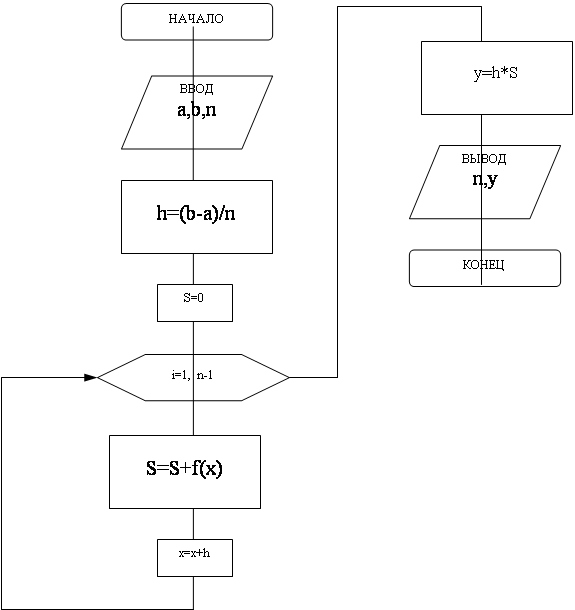
Блок-схема алгоритма решения задания №2.1
Вычисление определенного интеграла методом средних прямоугольников:
Текст программы вычисления
определенного интеграла методом
трапеции
program integral 2;
uses crt;
var a,b,h,S,S1,x,y: real;
i,n: integer;
function f (c: real): real;
begin
f: =1/sqr (3*sin (x) +2*cos (x));
end;
begin clrscr;
write ('a,b,n=');
readln (a,b,n);
h: = (b-a) /n;
x: =a;
s: =0;
for i: =1 to n-1 do
begin
x: =x+h;
s: =s+f (x);
end;
S1: = f (a) +f (b);
y: = (h/2) * (S1+2*s);
writeln ('n=',n, ' y=',y: 8: 3);
readkey;
end.
Результаты работы программы
a=0 b=1 n=1000 y=0.117
Блок-схема алгоритма решения задания № 2.2
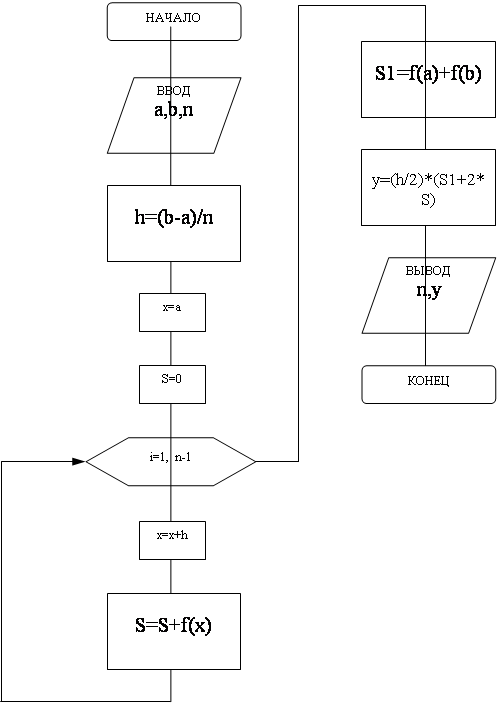 |
Вычисление определенного интеграла методом трапеции:
Текст программы вычисления
определенного интеграла
методом Симпсона
program simpson;
uses crt;
var a,b,h,x,y,s,s1: real;
i,n,c,m: integer;
function f (x: real): real;
begin
f: =1/sqr (3*sin (x) +2*cos (x));
end;
begin clrscr;
write ('a,b,n=');
readln (a,b,n);
h: = (b-a) / (2*n);
x: =a;
s: =0;
c: =1;
m: =2*n-1;
for i: =1 to m do
begin
x: =x+h;
s: =s+ (3+c) *f (x);
c: =-c;
end;
s1: =f (a) +f (b);
y: = (h/3) * (s1+s);
writeln ('y=',y: 10: 3,' n=',n);
readkey;
end.
Результаты работы программы
a=0 b=1 n=1000 y=0.117
Блок-схема алгоритма решения задания №2.3
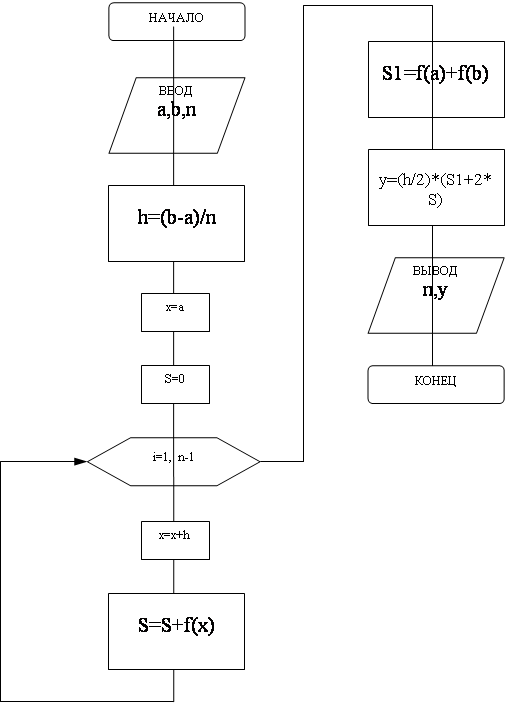 |
Вычисление определенного интеграла методом Симпсона:
![]() Текст программы вычисления
Текст программы вычисления
определенного интеграла с
автоматическим выбором шага
program avtomaticheskiyshag;
uses crt;
var e,a,b,s,h,sn,sn1: real;
i,n: integer;
function f (x: real): real;
var y: real;
begin
f: =1/sqr (3*sin (x) +2*cos (x));
end;
begin
clrscr;
write ('a='); read (a);
write ('b='); read (b);
write ('e='); read (e);
sn: =0;
sn1: =0;
n: =100;
repeat
n: =n*2;
h: = (b-a) /n;
s: =0;
sn: =sn1;
s: =s+f (a) +f (b);
for i: =1 to (n-1) do
s: =s+2*f (a+i*h);
s: = (h/2) *s;
sn1: =s;
until abs (sn-s) <e;
writeln ('s=',s: 8: 3);
readkey;
end.
Результаты работы программы
a=0 b=1 n=1000 s=0.117
Задание 3. Решение системы линейных уравнений Решение уравнения с помощью MathCAD
Данная задача в MathCAD будет выполнятся с использованием ранжированной переменной. В среде пакета MathCAD для выполнения итеративных вычислений предусмотрен аппарат ранжированных переменных.
Ранжированная переменная-это переменная, которой приписан диапазон изменения значений.
Пример ранжированной переменной:
x: =a,b. c,
где x - переменная, a,b,c - значения, которые принимает переменная, т.е. a-первое значение, b-второе значение, т.е. (b-a) - шаг изменения переменной, и c-последнее значение. .
Рассмотрим решение системы линейных уравнений матричным методом:
a11X1+a12X2+a13X3=b1,a21X1+a22X2+a23X3=b2,a31X1+a32X2+a33X3=b3.
Решение этим методом заключается в решении матричного уравнения вида:
R=M-1*V.
Для этого необходимо:
сформировать матрицу коэффициентов системы линейных уравнений
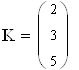
сформировать вектор-столбец коэффициентов свободных членов системы линейных уравнений V:
b1
V: = b2
b3
найти искомые параметры с помощью матричного уравнения: R=M-1*V.
получим:
X1
R = X2
X3
Рассмотрим решение системы линейных уравнений с помощью решающего блока Given - Find.
Для решения системы уравнений этим способом используется специальная конструкция, называемая решающим блоком. Блок состоит из заголовка (Given), его тела (определённой системы уравнений) конца блока (Find). Find включает в себя перечень переменных блока, относительно которых должна быть решена система уравнений.
Для решения этим методом введём начальные приближённые значения искомых значений:
X1: =0X2: =0X3: =0
опишем блок решения:
Given
x11X1+x12X2+x13X3=b1,x21X1+x22X2+x23X3=b2,x31X1+x32X2+x33X3=b3.
опишем ведущие переменные:
r: =find (X1, X2, X3)
найдём искомые параметры:
X1
r = X2
X3
Пример вычисления:
1) решение системы линейных уравнений матричным методом:
![]()
![]()
![]()


![]()
2) решение системы линейных уравнений с помощью решающего блока Given - Find.
![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()

Задание 4. Решение нелинейного уравнения
Задача нахождения корней нелинейных уравнений вида F (x) =0 встречается в различных областях научных исследований. Нелинейные уравнения можно разделить на два класса - алгебраические и трансцендентные. Алгебраическими уравнениями называются уравнения, содержащие только алгебраические функции. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.) называются трансцендентными.
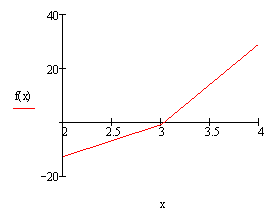
По условию задачи уравнение cosx-x+4=0 является трансцендентным. Поэтому для нахождения корней будем использовать приближённые методы вычисления (метод касательных и метод половинного деления).
Существуют различные итерационные методы решения трансцендентных уравнений. Наиболее известные: метод касательных, метод половинного деления, метод хорд, комбинированный метод хорд и касательных, метод итераций и т.д.
Метод половинного деления отрезка пополам является одним из простейших методов нахождения корней нелинейных уравнений. Метод довольно медленный, однако он всегда сходится, т.е. при использовании решение получается всегда, причём с заданной точностью. Требуемое обычно большее число итераций по сравнению с некоторыми другими методами не является препятствием к применению этого метода, если каждое значение функции несложно.
Метод касательных или метод Ньютона. В этом методе каждой итерации объём вычислений больший, чем в ранее рассмотренном методе половинного деления, поскольку приходится находить не только значение функции F (x), но и значения её производных. Однако скорость сходимости здесь значительно выше, чем в предыдущем методе.
Решение нелинейного уравнения в среде пакета MathCAD
По условию задачи данное нелинейное уравнение является трансцендентным. Для нахождения корней этого уравнения воспользуемся функцией root.
![]()
![]()
![]()
![]()
![]()
Решение трансцендентных уравнений методом касательных
program kasatelnie;
uses crt;
label 20;
var a,b,E,U,D,x: real;
function f (x: real): real;
begin
f: =u*u*u-7*u-7;
end;
function f1 (x: real): real;
begin
f1: =3*x*x-10;
end;
function f2 (x: real): real;
begin
f2: =6*x;
end;
begin
writeln ('a,b,E=');
read (a,b,E);
if f (a) *f2 (a) >0 then
u: =a else u: =b;
20: D: =f (u) /f1 (u);
u: =u-d;
if ABS (d) >E then goto 20;
writeln ('u=',u: 7: 3);
readkey;
end.
Результаты работы программы
a=2 b=4 e=0.01 x=3.000
Блок-схема алгоритма решения задания №4.2
 |
Метод касательных:
Решение трансцендентных уравнений методом деления отрезка пополам
Program polovinoedelenie;
uses crt;
label 20,30,40;
var a,b,E,V,W,X,Z: real;
function f (x: real): real;
begin
f: =x*x*x-7*x-7;
end;
begin
writeln ('a,b,E=');
read (a,b,E);
V: =f (a);
W: =f (b);
20: x: = (a+b) /2;
z: =f (x);
if z=0 then goto 30;
if V*Z>=0 then
begin
a: =x;
v: =z;
end;
begin
b: =x;
W: =z;
end;
40: if (b-a) >E then goto 20;
x: = (a+b) /2;
30: writeln ('x=',x: 6: 3);
readkey;
end.
Результаты работы программы
a=2 b=4 e=0.01 u=3.049
Блок-схема алгоритма решения задания №4.1
Метод деления отрезка пополам:

Задание 5. Организация нахождения минимума и максимума элемента в массиве случайных чисел в среде пакета MathCAD
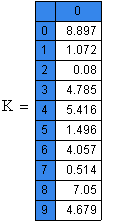
Организовать нахождение MIN и MAX элемента в массиве случайных чисел К. Генерацию элементов массива осуществить с помощью встроенной функции RND (N); вычисления провести с помощью встроенных функций MIN (К) и MAX (К)
В Mathcad:
Необходимое нахождение значений в среде MathCAD можно провести с помощью встроенных функций.
Для решения этой задачи нужно: задать промежуток, в котором будут генерироваться случайные числа; воспользоваться функцией rnd; после того, как будут выбраны случайные числа, воспользуемся функцией нахождения минимального и максимального значений: min (x) и max (x).
![]()
![]()
![]()
![]()

Задание 6
Определить среднее арифметическое, среднее квадратическое отклонение рядов Ni и Ki, дисперсию и коэффициент корреляции. Ввод Ni и Ki-в виде векторов из 10 элементов, каждый из внешних файлов данных, подготовленных вручную или с помощью любой программы, позволяющей создавать файлы в формате ASCIT. Вычисление - с помощью встроенных функций: mean (N), mean (K), var (N), var (K),stdev (K), stdev (K), corr (N,K).
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Похожие работы
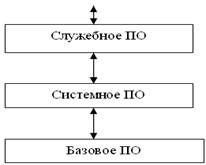
... (САПР) и пр.; - ПС, используемые в обучении – электронные учебники, тренажеры, тесты и пр.; - игровые программы; - программы, созданные пользователем с помощью сред программирования. Еще один класс программного обеспечения – специальное ПО. Основное его отличие от системного ПО в том, что пользователь сам решает, будет ли он использовать эти ПС или нет, а отличие ...
0 комментариев