Навигация
Метод исключения Гаусса для решения СЛАУ
1.3 Метод исключения Гаусса для решения СЛАУ
Суть всех методов исключения состоит в приведении исходной системы уравнений к системе более простого вида, для которой легко найти решение. К этим методам можно отнести метод исключения Гаусса, который имеет много вычислительных схем и, как показали исследования, является идеальным алгоритмом для решения СЛАУ.
Рассмотрим сначала самую простую схему – схему единственного деления. Применение схемы единственного деления продемонстрируем на примере СЛАУ 4- го порядка
![]()
![]()
![]()
![]()
Разделив первое уравнение системы на ![]() , получим
, получим
![]()
Из второго уравнения системы вычтем первое, умноженное на коэффициент при ![]() , то есть на
, то есть на ![]() . В результате получаем:
. В результате получаем:
![]()
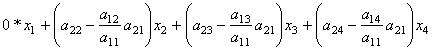
=![]()
![]()
![]()
Поступая таким же образом с третьим и последующими уравнениями системы, получим
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
![]() К выделенной системе применим тот же алгоритм, что и к исходной. В результате получаем
К выделенной системе применим тот же алгоритм, что и к исходной. В результате получаем
![]()
![]()
![]()
![]()
Прямой ход метода Гаусса закончен. Из полученной треугольной системы линейных алгебраических уравнений обратным ходом Гаусса отыскиваем вектор решения ![]() по следующим формулам
по следующим формулам
![]() ,
, ![]() ,
, ![]() .
.
В процессе построения методов Ньютона и секущих решения нелинейного скалярного уравнения ![]()
![]()
функция f(x) в окрестности текущей точки ![]() подменяется линейной функцией (аффинной моделью)
подменяется линейной функцией (аффинной моделью)
![]() . Приравнивание к нулю последней, т.е. решение линейного уравнения
. Приравнивание к нулю последней, т.е. решение линейного уравнения ![]() , порождает итерационную формулу
, порождает итерационную формулу ![]() для вычисления приближений к корню уравнения.
для вычисления приближений к корню уравнения.
Если потребовать, чтобы заменяющая функцию f(x) вблизи точки ![]() аффинная модель
аффинная модель ![]() имела в этой точке одинаковую с ней производную, то, дифференцируя, получаем значение коэффициента
имела в этой точке одинаковую с ней производную, то, дифференцируя, получаем значение коэффициента ![]() , подстановка которого в
, подстановка которого в ![]() приводит к известному методу Ньютона. Если же исходить из того, что наряду с равенством
приводит к известному методу Ньютона. Если же исходить из того, что наряду с равенством ![]() должно иметь место совпадение функций f(x) и
должно иметь место совпадение функций f(x) и ![]() в предшествующей
в предшествующей ![]() точке
точке ![]() т.е. из равенства
т.е. из равенства ![]() ,
, ![]() , получаем коэффициент
, получаем коэффициент ![]() , превращающий
, превращающий ![]() в известную формулу секущих.
в известную формулу секущих.
Равенство ![]() , переписанное в виде
, переписанное в виде ![]() , называют соотношением секущих в
, называют соотношением секущих в ![]() Оно легко обобщается на n -мерный случай и лежит в основе вывода метода Бройдена. Опишем этот вывод.
Оно легко обобщается на n -мерный случай и лежит в основе вывода метода Бройдена. Опишем этот вывод.
В n-мерном векторном пространстве ![]() соотношение секущих представляется равенством
соотношение секущих представляется равенством
![]() ,
,
где ![]() - известные n-мерные векторы,
- известные n-мерные векторы, ![]() - данное нелинейное отображение, а
- данное нелинейное отображение, а ![]() - некоторая матрица линейного преобразования в
- некоторая матрица линейного преобразования в ![]() . С обозначениями
. С обозначениями ![]() ,
, ![]() соотношение секущих в
соотношение секущих в ![]() обретает более короткую запись
обретает более короткую запись ![]() . Аналогично одномерному случаю, а именно, по аналогии с формулой
. Аналогично одномерному случаю, а именно, по аналогии с формулой ![]() , будем искать приближения к решению
, будем искать приближения к решению ![]() векторного уравнения
векторного уравнения ![]() по формуле
по формуле ![]() . Обратимую n x n-матрицу
. Обратимую n x n-матрицу ![]() в ней нужно подобрать так, чтобы она удовлетворяла соотношению секущих
в ней нужно подобрать так, чтобы она удовлетворяла соотношению секущих ![]() . Но это соотношение не определяет однозначно матрицу
. Но это соотношение не определяет однозначно матрицу ![]() : глядя на равенство
: глядя на равенство ![]() , легко понять, что при n>1 существует множество матриц
, легко понять, что при n>1 существует множество матриц ![]() , преобразующих заданный n-мерный вектор
, преобразующих заданный n-мерный вектор ![]() в другой заданный вектор
в другой заданный вектор ![]() (отсюда - ясность в понимании того, что могут быть различные обобщения одномерного метода секущих).
(отсюда - ясность в понимании того, что могут быть различные обобщения одномерного метода секущих).
При формировании матрицы ![]() будем рассуждать следующим образом. Переходя от имеющейся в точке
будем рассуждать следующим образом. Переходя от имеющейся в точке ![]() аффинной модели функции F(x)
аффинной модели функции F(x) ![]() к такой же модели в точке
к такой же модели в точке ![]()
![]() мы не имеем о матрице линейного преобразования
мы не имеем о матрице линейного преобразования ![]() никаких сведений, кроме соотношения секущих
никаких сведений, кроме соотношения секущих ![]() . Поэтому исходим из того, что при этом переходе изменения в модели должны быть минимальными. Эти изменения характеризует разность
. Поэтому исходим из того, что при этом переходе изменения в модели должны быть минимальными. Эти изменения характеризует разность ![]() . Вычтем из равенства
. Вычтем из равенства ![]() определяющее
определяющее ![]() равенство
равенство ![]() и преобразуем результат, привлекая соотношение секущих
и преобразуем результат, привлекая соотношение секущих ![]() . Имеем:
. Имеем:
![]()
Представим вектор ![]() в виде линейной комбинации фиксированного вектора
в виде линейной комбинации фиксированного вектора ![]() определенного в
определенного в ![]() , и некоторого вектора t, ему ортогонального:
, и некоторого вектора t, ему ортогонального: ![]() ,
, ![]()
Подстановкой этого представления вектора ![]() в разность
в разность ![]() получаем другой ее вид
получаем другой ее вид ![]()
Анализируя выражение ![]() , замечаем, что первое слагаемое в нем не может быть изменено, поскольку
, замечаем, что первое слагаемое в нем не может быть изменено, поскольку ![]() - фиксированный вектор при фиксированном k. Поэтому минимальному изменению аффинной модели
- фиксированный вектор при фиксированном k. Поэтому минимальному изменению аффинной модели ![]() будет отвечать случай, когда второе слагаемое в
будет отвечать случай, когда второе слагаемое в ![]() будет нуль-вектором при всяких векторах t, ортогональных векторам
будет нуль-вектором при всяких векторах t, ортогональных векторам ![]() , т.е.
, т.е. ![]() следует находить из условия
следует находить из условия ![]()
![]()
Непосредственной проверкой убеждаемся, что условие ![]()
![]() будет выполнено, если матричную поправку
будет выполнено, если матричную поправку ![]() взять в виде одноранговой nхn-матрицы
взять в виде одноранговой nхn-матрицы ![]() .
.
Таким образом, приходим к так называемой формуле пересчета С. Бройдена
![]()
Похожие работы
... - функции f. Дальше, имеем: . Отсюда , где W'(x) - транспонированная матрица Якоби. Поэтому окончательно , причем . 3. Программная реализация итерационных методов Реализация алгоритмов итерационных методов решения систем нелинейных уравнений будет показана на примере системы: 3.1 Метод простых итераций Приведём систему к виду: Проверим условие ...
... В состав системы включены следующие интерфейсные программы: COSMOS/M DESIGNER. Автономная интерфейсная программа для системы AutoCAD. Она позволяет вызывать на выполнение вычислительные модули программы COSMOS/M прямо из среды AutoCAD через дополнительное меню. (AutoCAD продукция Autodesk, Inc.) COSMOS/M ENGINEER. Автономная интерфейсная программа для системы Рго/ENGINEER на рабочих станциях ...
... сети, позволяющая реализовать автоматическое изменение числа нейронов в зависимости от потребностей задачи, позволяет не только исследовать, но и контролировать процесс воспитания психологической интуиции искусственных нейронных сетей. - Впервые применена выборочная константа Липшица для оценки необходимой для решения конкретной задачи структуры нейронной сети. Практическая значимость ...


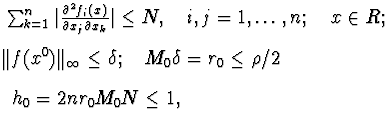
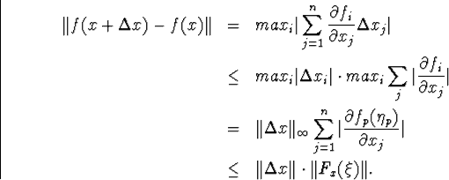
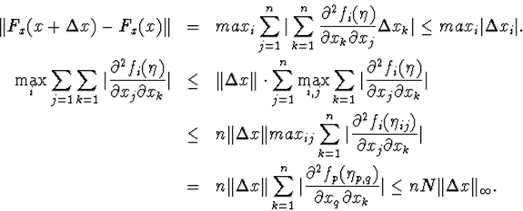

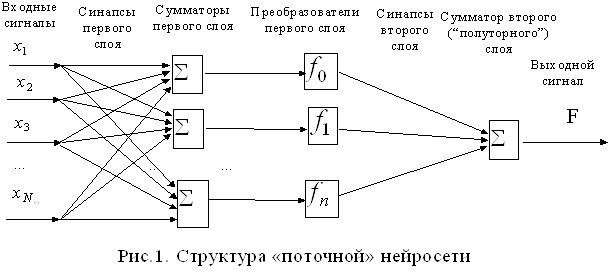

0 комментариев