РАЗРАБОТКА ПРОГРАММЫ И ИСЛЕДОВВАНИЕ РЕЗУЛЬТАТА ЕЕ РАБОТЫ

2. РАЗРАБОТКА ПРОГРАММЫ И ИСЛЕДОВВАНИЕ РЕЗУЛЬТАТА ЕЕ РАБОТЫ

Задача. Разработать программу, реализующую метод Бройдена.

Структура программы. Программа была разработана в интегрированной среде разработке приложений Microsoft Visual Studio 2008 на языке программирования C#, проект программы Console Application. В ходные данные программы начальный вектор решения, начальная матрица Якоби и удовлетворяющая погрешность. Программа решает систему уравнений 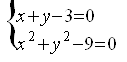. Если программа не находит решения удовлетворяющего требуемой точности за 10 итераций, то поиск решения прекращается, а так же если процесс расходится (в соответствии с приложением А).

Введем матрицу Якоби , погрешность 0,3 начальное решение является точным решение. На 1 итерации получаем результат решения (рисунок 1).

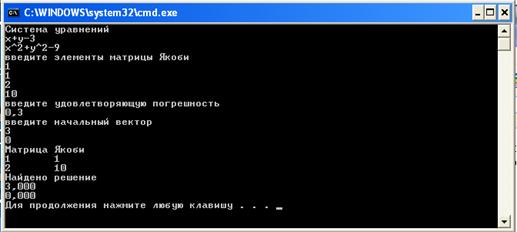
Рисунок 1 – Первый пример работы программы

Результат точное решение на 1 шаге. Попробуем задать начальное решение отличное от точного (рисунок 2).

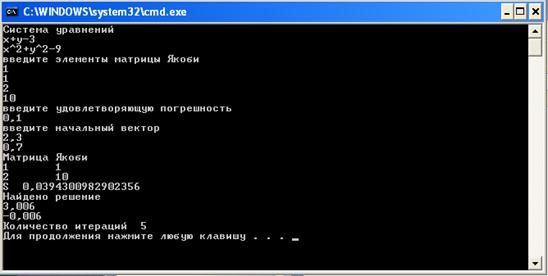
Рисунок 2 – второй пример работы программы

Получили близко решение к точному решению. Попробуем уменьшить погрешность (рисунок 3).

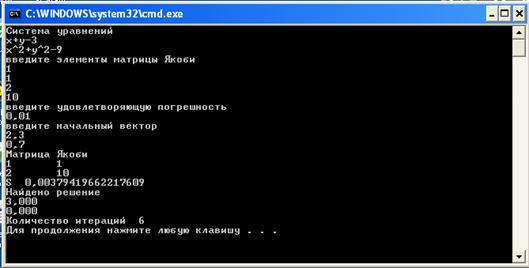
Рисунок 3 – третий пример работы программы

Получили точное решение. Попробуем сильнее отойти в начальном решении от точного (рисунок 4).

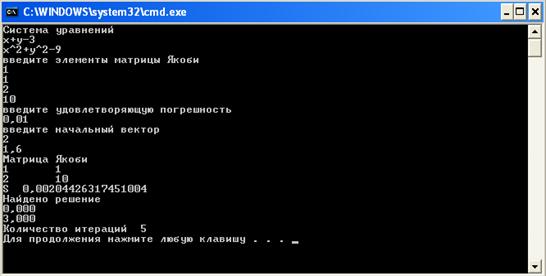
Рисунок 4 – Четвертый пример работы программы

Получаем точное решение. Уменьшим погрешность и сильнее отойдем от точного решения. Теперь начальное решение произвольное (рисунок 5).

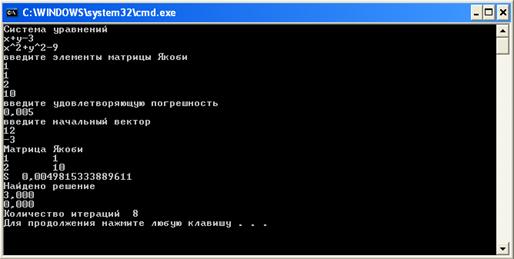
Рисунок 5 – Пятый пример работы программы

Видим увеличение количества итераций. Решение получили точное. Немного изменим начальную матрицу Якоби (рисунок 6).

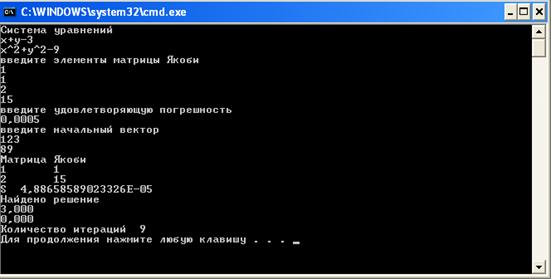
Рисунок 6 – Шестой пример работы программы

Увеличение количества итераций. Решение точное. Теперь возьмем другую матрицу Якоби (рисунок 7).

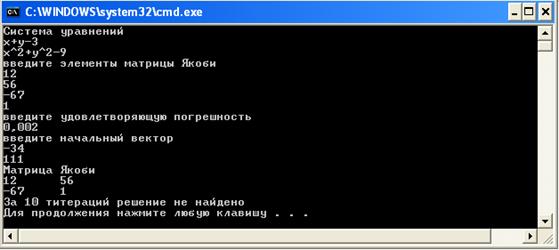
Рисунок 7 – Седьмой пример работы программы

Получили плохой результат решения. Попробуем выяснить из-за чего. Или матрица Якоби в начале исследования была близка к расчетной матрицы Якоби на основе конечно разностной аппроксимации производных или при таком начальном решении требуется слишком много итераций.

Попробуем с начальной матрицей Якоби. Процесс решения стал расходится. Делаем вывод, что не смогли найти решения из-за начального решения (рисунок 8).

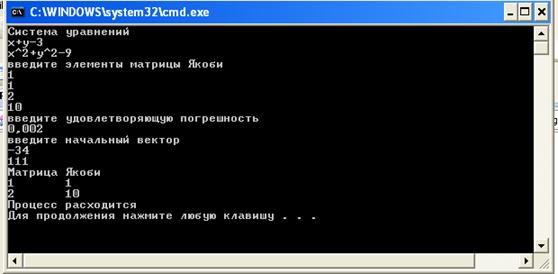
Рисунок 8 – Восьмой пример работы программы

На основе рисунка 9, рисунка 10 и рисунка 11 видим, что наша первая матрица Якоби была удачно выбрана.

Матрица Якоби близка к первой матрице Якоби (рисунок 12).

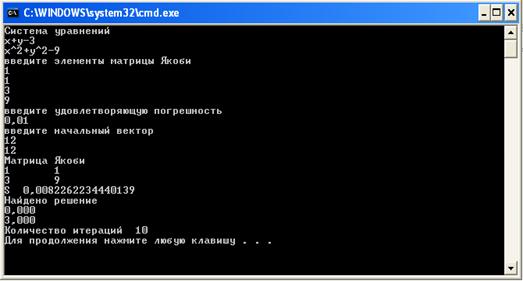
Рисунок 9 – Девятый пример работы программы

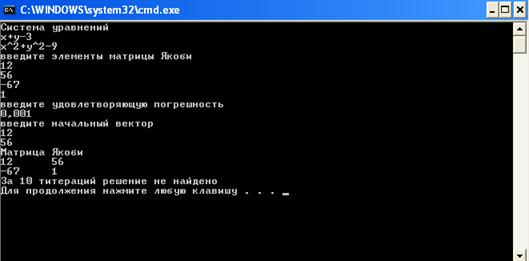
Рисунок 10 – Десятый пример работы программы

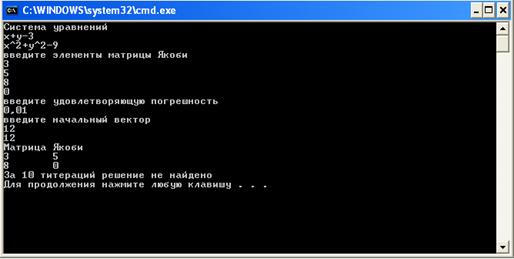
Рисунок 11 – Одиннадцатый пример работы программы

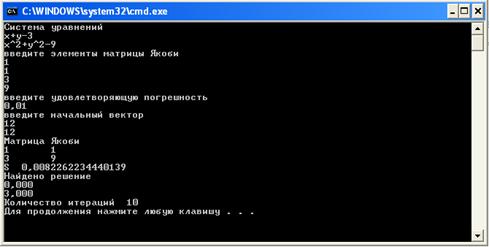
Рисунок 12 – Двенадцатый пример работы программы

Попробуем изменить систему уравнений, решаемую программой и посмотрим на результаты работы программы (рисунок 13,14).

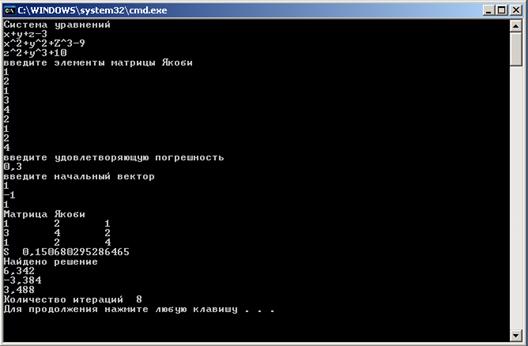
Рисунок 13 – Тринадцатый пример работы программы

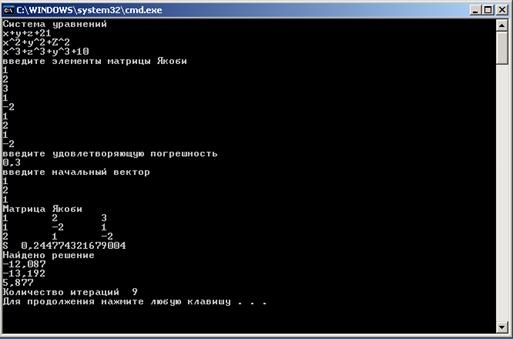
Рисунок 14 – Четырнадцатый пример работы программы

ЗАКЛЮЧЕНИЕ

Если начальное приближение выбрано достаточно близко к решению и если начальная аппроксимация матрицы Якоби достаточно точна, то метод Бройдена обладает сверхлинейной сходимостью, но не квадратичной, как метод Ньютона.

Данная курсовая работа выполнена в полном объеме. В курсовой работе был рассмотрен метод Бройдена, написана программа реализующая его.

СПИСОК ЛИТЕРАТУРЫ

1.    С.Л. Подвальный, Л.В. Холопкина. Вычислительная математика- учебное пособие ВГТУ, 2004 - 147 с.

2.    Методы решения систем нелинейных уравнений. Метод Ньютона. Его реализации и модификации. - Электрон. дан. – Режим доступа: www.exponenta.ru/educat/referat/XVkonkurs/15/index.asp.

ПРИЛОЖЕНИЕ

Текст программы

/*программа предназначена для решения системы нелинейных уравнений.

Программа выполнена 1 ноября 2009 года. Обем необходимой памяти для работы составляет 124 КБ. Версия программы №1.Автор Харитонова Яна Андреевна.*/

using System;

using System.Collections.Generic;

using System.Linq;

using System.Text;

namespace Broiden

{

class Program

{

static void Main(string[] args)

{

int N = 2;

Console.WriteLine("Система уравнений");

Console.WriteLine("x+y-3" + "\n" + "x^2+y^2-9");

double[,] yakob = new double[N, N];

Console.WriteLine("введите элементы матрицы Якоби");

for (int i = 0; i < N; i++)

{

for (int j = 0; j < N; j++)

{

yakob[i, j] = Convert.ToDouble(Console.ReadLine());

}

}

double[] V = new double[N];

double[] B = new double[N];

double[] Bnach = new double[N];

double e;

Console.WriteLine("введите удовлетворяющую погрешность ");

e = Convert.ToDouble(Console.ReadLine());

Console.WriteLine("введите начальный вектор");

for (int i = 0; i < N; i++)

{

[i] = Convert.ToDouble(Console.ReadLine());

}

int maunI = 0;

int naid = 0;

int stop = 0;

double S=0;

Console.WriteLine("Матрица Якоби");

for (int i = 0; i < N; i++)

{

for (int j = 0; j < N; j++)

{

Console.Write(yakob[i, j] + "\t");

}

Console.WriteLine();

}

while ((maunI != 10) && (naid != 1) && (stop != 1))

{

maunI++;

Bnach[0] = V[0] + V[1] - 3;

Bnach[1] = V[0] * V[0] + V[1] * V[1] - 9;

int iter = 0;

double[,] A = new double[N, N];

for (int i = 0; i < N; i++)

{

for (int j = 0; j < N; j++)

{

A[i, j] = yakob[i, j];

}

}

while (iter != N - 1)

{

for (int h = 0; h < N; h++) { B[h] = Bnach[h] * (-1); }

double pomny = A[iter, iter];

for (int j = iter; j < N; j++)

{

A[iter, j] = A[iter, j] / pomny;

}

B[iter] = B[iter] / pomny;

for (int i = iter + 1; i < N; i++)

{

double zap = A[i, iter];

for (int j = iter; j < N; j++)

{

A[i, j] = A[i, j] - A[iter, j] * zap;

}

B[i] = B[i] - B[iter] * zap;

}

iter++;

}

double[] X = new double[N];

if (A[N - 1, N - 1] != 0)

{ X[N - 1] = B[N - 1] / A[N - 1, N - 1]; }

else X[N - 1] = 0;

double SYM = 0;

int l = N - 2;

for (int i = N - 2; i >= 0; i--)

{

SYM = 0;

for (int j = i + 1; j <= N - 1; j++)

{

SYM = SYM + A[i, j] * X[j];

}

if (A[i, l] != 0)

{ X[i] = (B[i] - SYM) / A[i, l]; }

else X[i] = 0;

l--;

}

double[] XJ = new double[N];

double promq = 0; double mq = 0; double nq = 0;

S = 0;

for (int i = 0; i < N; i++)

{

XJ[i] = V[i] + X[i];

if (X[i] >= 0)

{ promq = X[i] + promq; }

else {promq = -X[i] + promq; }

if (V[i] >= 0)

{ mq = mq + V[i]; }

else

{ mq = mq - V[i]; }

if (XJ[i] >= 0)

{ nq = nq + XJ[i]; }

else { nq = nq - XJ[i]; }

}

if (mq != 0) { S = promq / mq; }

else { S = promq / nq; }

if (S < 0) { S = -S; }

if (S < e)

{

Console.WriteLine("S "+S);

naid = 1;

Console.WriteLine("Найдено решение");

for (int i = 0; i < N; i++)

{

Console.WriteLine("{0:n3}", XJ[i]);

}

Console.WriteLine("Количество итераций " + maunI);

}

else

{

if (S > 20) { Console.WriteLine("Процесс расходится"); stop = 1; }

else

{

if (maunI = 10) { Console.WriteLine("За 10 титераций решение не найдено"); }

else

{

double[] Y = new double[N];

Y[0] = (XJ[0] + XJ[1] - 3) - Bnach[0];

Y[1] = (XJ[0] * XJ[0] + XJ[1] * XJ[1] - 9) - Bnach[1];

double[,] J = new double[N, N];

for (int i = 0; i < N; i++)

{

for (int j = 0; j < N; j++)

{

J[i, j] = yakob[i, j];

yakob[i, j] = 0;

}

}

double[] ymnMAS = new double[N]; double[] PRMAS = new double[N];

for (int i = 0; i < N; i++)

{

double Ymn = 0;

for (int j = 0; j < N; j++)

{

Ymn = Ymn + J[i, j] * X[j];

}

ymnMAS[i] = Ymn;

PRMAS[i] = Y[i] - ymnMAS[i];

}

double del = 0;

for (int i = 0; i < N; i++) { del = del + X[i] * X[i]; }

for (int i = 0; i < N; i++)

{

for (int j = 0; j < N; j++)

{

yakob[i, j] = J[i, j] + ((PRMAS[i] * X[j]) / del);

}

}

for (int i = 0; i < N; i++)

{ V[i] = XJ[i]; }

}

}

}

}

}

}

}