Навигация
Решение транспортной задачи методом потенциалов
Министерство Российской Федерации по атомной энергии
Саровский Государственный Физико-Технический Институт
Политехникум СарФТИ
КУСОВАЯ РАБОТА
По специальности– «Программное обеспечение»
Тема: Решение транспортной задачи методом потенциалов
Студент:
Группа:
Преподаватель:
Дата: 05 Мая
Оценка:…
г. Саров
2005 г.
Содержание
Введение.. 3
1. Транспортная задача.. 4
1.1 Составление опорного плана. 7
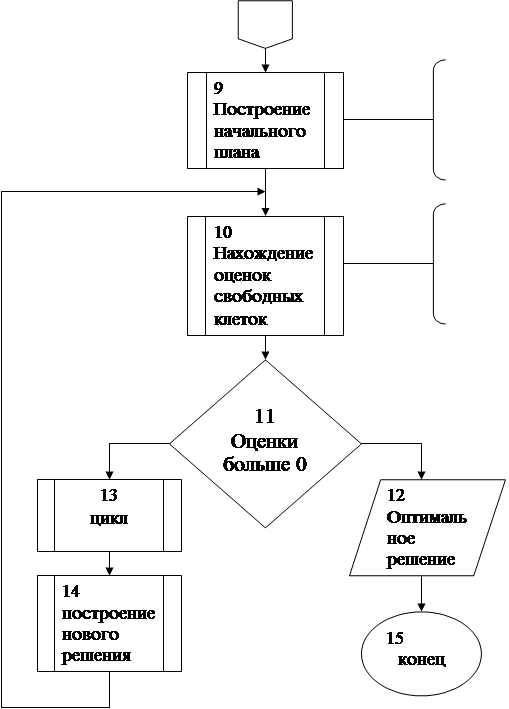
1.2 Метод потенциалов. 9
2. Практическая часть.. 16
2.1 Обоснование выбора языка программирования. 16
2.2 Разработка. 16
2.3 Руководство пользователей. 16
Заключение.. 18
Литература.. 19
Введение
Данный курсовой проект представляет собой программу для решения транспортной задачи методом потенциалов. Программа предоставляет пользователю возможность пошагового нахождения оптимального решения. Все промежуточные результаты выводятся на экран, пользователь может следить за ходом решения.
Транспортная задача заключается в нахождении такого плана поставок, при котором его цена минимальна.
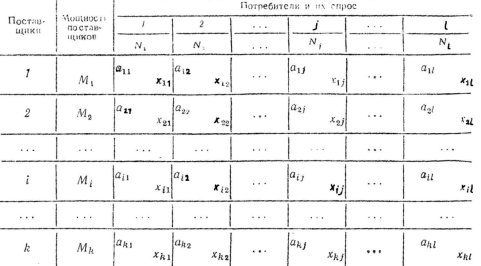
Условия задачи задаются в виде таблицы:
| поставщик | потребитель | Запас груза | |||
| В1 | В2 | … | Вn | ||
| А1 | C11 X11 | C12 X12 | … | C1n X1n | a1 |
| А2 | C21 X21 | C22 X22 | … | C2n X2n | a2 |
| … | … | … | … | … | … |
| Аm | Cm1 Xm1 | Cm2 Xm2 | … | Cmn Xmn | am |
| Потребность в грузе | b1 | b2 | … | bn | |
Матрица (cij)m*n называется матрицей тарифов. Планом транспортной задачи называется матрица х=(xij)m*n, где каждое число обозначает количество единиц груза, которое надо доставить из i–го пункта отправления в j–й пункт назначения.
1. Транспортная задача
Транспортная задача ставится следующим образом: имеется m пунктов отправления, в которых сосредоточены запасы каких-то однородных грузов. Имеется n пунктов назначения подавшие заявки соответственно на груза. Известны стоимости рijперевозки единицы груза от каждого пункта отправления до каждого пункта назначения. Все числа рij, образующие прямоугольную таблицу заданы. Требуется составить такой план перевозок (откуда, куда и сколько единиц поставить), чтобы все заявки были выполнены, а общая стоимость всех перевозок была минимальна.
Далее, предполагается, что
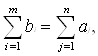 (1)
(1)
где bi есть количество продукции, находящееся на складе i, и aj – потребность потребителя j.
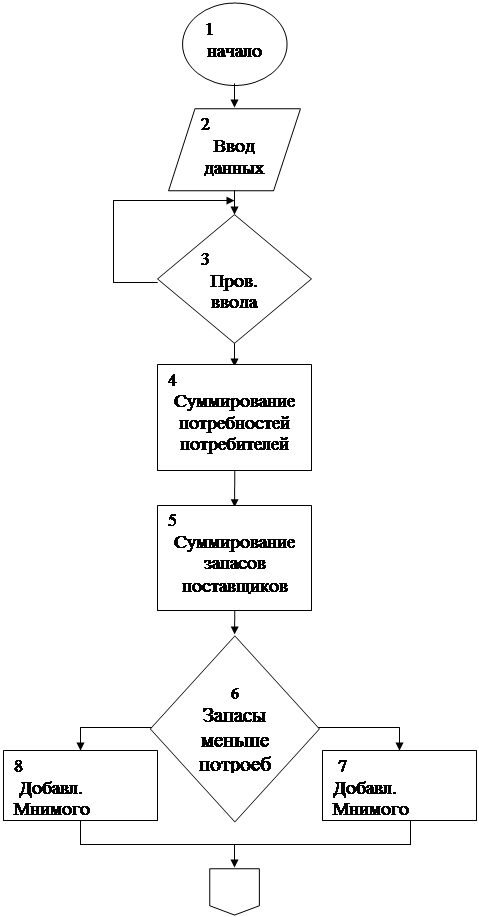
Замечание. Если ![]() то количество продукции, равное
то количество продукции, равное ![]() остается на складах. В этом случае мы введем "фиктивного" потребителя n +1 с потребностью
остается на складах. В этом случае мы введем "фиктивного" потребителя n +1 с потребностью ![]() и положим транспортные расходы pi,n+1 равными 0 для всех i.
и положим транспортные расходы pi,n+1 равными 0 для всех i.
Если ![]() то потребность не может быть покрыта. В этом случае начальные условия должны быть изменены таким образом, чтобы потребность в продукции могла быть обеспечена.
то потребность не может быть покрыта. В этом случае начальные условия должны быть изменены таким образом, чтобы потребность в продукции могла быть обеспечена.
Обозначим через xij количество продукции, поставляемое со склада i потребителю j. В предложении (1) нам нужно решить следующую задачу (математическая модель транспортной задачи):
![]()
![]() (2)
(2)
![]()
![]()
![]()
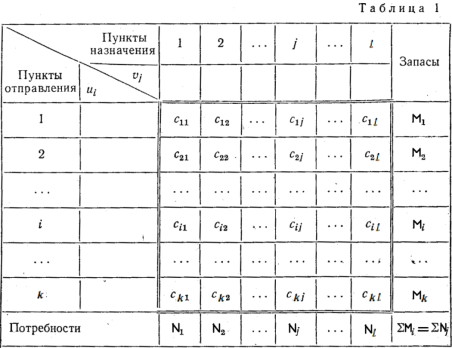
Транспортную задачу мы можем характеризовать транспортной таблицей и таблицей издержек:
| а1 | … | аn | ||||
| b1 . . . bm | . | |||||
| . | ||||||
| . | ||||||
| . | ||||||
| . | ||||||
| . | ||||||
| p11 | … | p1n |
| . | . | |
| . | . | |
| . | . | |
| pm1 | … | pmn |
Допустимый план перевозок будем представлять в виде транспортной таблицы:
| а1 | … | аn | |
| b . . . bm |
| … |
|
| . | . | ||
| . | . | ||
| . | . | ||
|
| … |
|
Cумма элементов строки i должна быть равна bi, а сумма элементов столбца j должна быть равна aj, и все ![]()
![]() должны быть неотрицательными.
должны быть неотрицательными.
Пример 1.
| 20 | 5 | 10 | 10 | 5 | |
| 15 | |||||
| 15 | |||||
| 20 |
| 5 | 6 | 3 | 5 | 9 |
| 6 | 4 | 7 | 3 | 5 |
| 2 | 5 | 3 | 1 | 8 |
Мы получаем следующую задачу:
х11+х12+х13+х14+х15 =15,
х21+х22+х23+х24+х55 =15,
х31+х32+х33+х34+х35 =20,
х11 +х21 +х31=20,
х12+х22 +х32=5,
х13+х23 +х33 =10,
х14 +х24 +х34 =10,
х15+х25+х35=5;
хij
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... метод потенциалов. Однако на распределительном методе основаны некоторые другие способы решения задач, что и вызывает необходимость его изучения. [5] 9. Метод потенциалов Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид. Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая ...
... Ai в Bj равна Cij; таблица стоимостей задана. Требуется найти план перевозок xij, который удовлетворял бы балансовым условиям и при этом стоимость всех перевозок бала минимальна. Идея метода потенциалов для решения транспортной задачи сводиться к следующему. Представим себе что каждый из пунктов отправления Ai вносит за перевозку единицы груза (всё равно куда) какую-то сумму ai; в свою ...
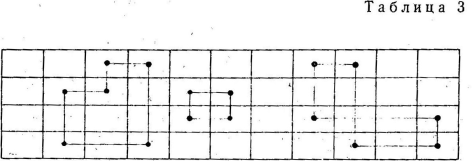
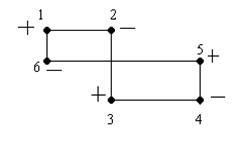
... . Система векторов условий транспортной задачи линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимое решение транспортной задачи , i=1,2,…,m; j=1,2,…,n является опорным только в том случае, когда из занятых им клеток таблицы нельзя образовать ни одного цикла. Метод вычеркивания. Для проверки возможности ...





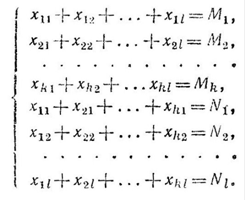

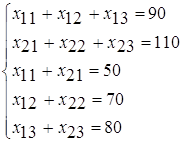
0 комментариев