Навигация
ЗМІСТ
Вступ
1. Теоретична частина.
1.1 Постановка задачі.
1.2 Методи розв'язування задачі
2. Практична частина
2.1 Архітектура програми
2.2 Опис програми
2.3 Контрольний приклад та аналіз результатів машинного експерименту.
Висновки
Список використаної літератури.
Додатки
Вступ
Центральним поняттям програмування є, безперечно, поняття алгоритму. З нього починається робота над програмою і від якості алгоритму залежить її успішне створення. Тому вміння програмувати в значній мірі означає розробляти хороші алгоритми і застосовувати вже відомі.
На сьогодні існує велика кількість різноманітних мов програмування, кожна з яких має свої певні переваги та недоліки. В цьому розмаїтті не завжди легко зробити свій вибір на користь якоїсь певної мови програмування.
Для реалізації поставленої задачі вибрано середовище Turbo Pascal. Алгоритмічна мова Паскаль була створена Н.Віртом на початку 70-х років. Завдяки зусиллям розробників ця мова програмування стала потужним інструментом професійних програмістів‚ не втративши простоти і ясності, властивих цій мові від народження.
Розробник системи Turbo Pascal - фірма Borland International виникла в 1984 році і за порівняно короткий час неодноразово дивувала користувачів персональних ЕОМ своїми Turbo системами. Було випущено кілька версій Turbo Pascal: 3.0‚ 4.0‚ 5.0‚ 5.5‚ 6.0‚ 7.0‚ Pascal for Windows, Borland Pascal.
Головні особливості середовища Turbo Pascal:
Ø широкий спектр типів даних‚ можливість обробки рядкових та структурних типів даних;
Ø достатній набір операторів управління розгалуженнями та циклами;
Ø добре розвинутий апарат підпрограм та зручні конструкції роботи з файлами;
Ø великі можливості управління усіма ресурсами ПЕОМ;
Ø різноманітні варіанти стикування з мовою Асемблера;
Ø підтримка ідей об'єктно-орієнтованого програмування (ООП).
Саме з огляду на ці особливості програмна реалізація курсового проекту було здійснено в середовищі Turbo Pascal.
Розробник системи програмування Turbo Pascal - фірма Borland International виникла в 1984 році і за порівняно короткий час неодноразово дивувала користувачів персональних ЕОМ своїми Turbo системами. Було випущено на ринок програмних продуктів декілька версій Turbo Pascal: 3.0, 4.0, 5.0, 5.5, 6.0, 7.0, Pascal for Windows, Borland Pascal.
Курсовий проект складається зі вступу, двох розділів, висновків, списку використаної літератури, графічної частини та додатків. Текст пояснювальної записки набрано та роздруковано з використанням текстового редактора Word. Графічна частина виконана з допомогою графічного редактора Visio.
1. Теоретична частина
1.1 Постановка задачі
У наукових дослідженнях часто для встановлення справедливості певного факту висловлюють гіпотези‚ які можна перевірити статистично‚ тобто виходячи з результатів спостережень випадкової вибірки з генеральної сукупності.
Сукупність усіх можливих значень досліджуваної величини (ознаки) називають генеральною сукупністю. Генеральна сукупність може бути скінченною і нескінченною. Результати обмеженого ряду спостережень ![]() випадкової величини Х називають вибіркою з генеральної сукупності. Кількість елементів вибірки називають її обсягом‚ а окреме значення ознаки - варіантою. Число‚яке показує‚ скільки разів варіанта зустрічається у вибірці‚ називають частотою. Сума всіх частот вибірки дорівнює її обсягу. Щоб вивчити закономірності частоти появи варіант‚ їх розміщують у зростаючому або спадаючому порядку і вказують частоту появи кожної варіанти у вибірці. При цьому отримують таблицю‚ яка називається варіаційним рядом‚ або емпіричним рядом.
випадкової величини Х називають вибіркою з генеральної сукупності. Кількість елементів вибірки називають її обсягом‚ а окреме значення ознаки - варіантою. Число‚яке показує‚ скільки разів варіанта зустрічається у вибірці‚ називають частотою. Сума всіх частот вибірки дорівнює її обсягу. Щоб вивчити закономірності частоти появи варіант‚ їх розміщують у зростаючому або спадаючому порядку і вказують частоту появи кожної варіанти у вибірці. При цьому отримують таблицю‚ яка називається варіаційним рядом‚ або емпіричним рядом.
Варіаційні ряди дають уявлення про варіацію ознаки у вибірковій сукупності. Для повнішої характеристики вибірки використовують узагальнюючі числові характеристики. Характеристики розподілів ймовірностей у генеральній сукупності називають параметрами‚а вибіркові (емпіричні) характеристики - оцінками‚ або статистиками.
Нехай маємо експериментальні значення ![]() випадкової величини (ознаки) Х‚ тоді можемо визначити деякі вибіркові статистики.
випадкової величини (ознаки) Х‚ тоді можемо визначити деякі вибіркові статистики.
Середнє значення визначаємо за формулою
![]() ‚ (1)
‚ (1)
яке є наближеним значенням (оцінкою) математичного сподівання М(Х) ознаки Х генеральної сукупності. Якщо за даними спостереження побудовано варіаційний ряд‚ то вводять поняття середньої зваженої
![]() ‚ (2)
‚ (2)
де ![]() - варіанта‚ якщо ряд дискретний і центр інтервалу‚ якщо ряд інтервальний;
- варіанта‚ якщо ряд дискретний і центр інтервалу‚ якщо ряд інтервальний; ![]() - частота варіанти або статистична вага‚
- частота варіанти або статистична вага‚ ![]() - кількість інтервалів.
- кількість інтервалів.
Характеристикою розсіяння навколо середньої є емпірична дисперсія‚ яку визначають за формулою
![]() . (3)
. (3)
Середнім квадратичним відхиленням називають корінь квадратний з дисперсії:
![]() . (4)
. (4)
Середнє квадратичне має ту розмірність‚ що й значення ознаки і є абсолютною характеристикою коливання ознаки навколо середнього значення.
Під статистичною гіпотезою розуміють будь-яке твердження щодо генеральної сукупності‚ яке перевіряється на основі вибірки. Статистичні гіпотези висловлюють як щодо законів розподілу‚ так і відносно параметрів розподілу. Наприклад‚ гіпотеза про те‚ що число відмов у телефонній мережі підпорядкований розподілу Пуассона‚ є гіпотезою про закон розподілу. Гіпотеза про те‚ що середні розміри деталей‚ які виготовляються на однотипних‚ паралельно працюючих станках‚ приблизно однакові‚ є гіпотезою про параметри розподілу.
Зроблений на основі статистичних даних висновок про те‚ що між кількома генеральними сукупностями або між емпіричним і теоретичним розподілом істотних відмінностей немає‚ називають нульовою (основною) гіпотезою. Гіпотезу‚ яка заперечує основну‚ називають альтернативною гіпотезою. Нульову гіпотезу зазвичай позначають літерою H0‚ альтернативну - літерою H1.
В результаті перевірки статистичної гіпотези‚ яка ґрунтується на статистичних спостереженнях‚ можна прийняти або відхилити нульову гіпотезу. Помилкове рішення можна допустити в обидвох випадках. Тому розрізняють помилки двох видів. Помилка першого виду полягає в тому‚ що нульова гіпотеза заперечується‚ тоді як насправді вона правильна. Помилка другого виду полягає в тому‚ що нульова гіпотеза приймається‚ тоді як правильною є альтернативна гіпотеза.
Ймовірність допустити помилку першого типу називають рівнем значущості і позначають грецькою літерою α. Рівень значущості встановлює дослідник залежно від важливості досліджуваної задачі. Рівень значущості - це та мінімальна ймовірність‚ починаючи з якої можна вважати подію практично неможливою. Найчастіше рівень значущості беруть рівним 0,05 або 0,01‚ значно рідше 0,1.
Є два типи задач перевірки гіпотез. Задачі першого типу пов'язані з перевіркою гіпотез про достовірність істотної відмінності між параметрами статистичних сукупностей. Відмінність між параметрами статистичних сукупностей вважають істотною‚ якщо вона перевищує ту‚ яку б можна було б пояснити випадковими коливаннями. Прикладом задачі першого типу є‚ наприклад‚ оцінка достовірності істотної відмінності між дисперсіями дох вибірок або між їх середніми значеннями.
Задачі другого типу пов'язані з оцінкою ступеня розбіжності емпіричного та теоретичного розподілів. Прикладом задачі цього типу може бути перевірка гіпотези про те‚ що емпіричний розподіл узгоджується з нормальним законом розподілу.
Перевірка гіпотези полягає в тому‚ що з вибірковими даними обчислюються значення деякої величини‚ яка має відомий стандартний розподіл (нормальний‚ Пуассона‚ Стьюдента‚ Пірсона та ін.). Цю величину називають статистикою критерію або просто значенням критерію.
Якщо обчислене за вибіркою значення критерію не перевищує граничного (критичного) значення‚ взятого з відповідних таблиць‚ то нульову гіпотезу визнають за вірну при заданому рівні значущості α. У цьому разі отриману за вибірковими даними відмінність можна пояснити тільки випадковістю вибірки. Але прийняття гіпотези зовсім не означає‚ що рівність параметрів генеральних сукупностей доведена‚ або те‚ що теоретичний закон відповідає емпіричному розподілу. Наявний статистичний матеріал не дає підстав про відхилення нульової гіпотези. Якщо обчислене значення критерію буде більше ніж критичне значення при заданому рівні значущості α‚ то відмінність генеральних сукупностей не модна пояснити тільки випадковістю вибірки. У цьому разі нульову гіпотезу відхиляють і кажуть‚ що при заданому рівні значущості відмінність є істотною.
Для статистичної перевірки гіпотез використовують ряд критеріїв: Фішера‚ Колмогорова_Смірнова‚ Стьюдента‚ Краскалла-Уолліса‚ Манна-Уїтні‚ Бартлета‚ Спірмена та ін.
В даному курсовому проекті реалізовано задачу побудови теоретичного ряду за розподілом Пуассона і обчислення ступеня згоди цього ряду з емпіричним за критерієм ![]() (хі-квадрат) Пірсона.
(хі-квадрат) Пірсона.
Похожие работы
... ів. Негативно класифіковані активи – це «сумнівна» та «безнадійна» заборгованість за основною сумою боргу, прострочені понад 31 день та сумнівні відсотки. 2.2 Міжнародні підходи щодо класифікації кредитного портфеля банку В процесі багатовікового та динамічного розвитку банківської системи створювались все нові підходи до класифікації кредитного портфеля, що дає змогу банкам оцінити якість ...
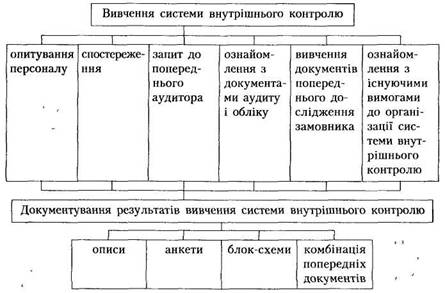
... ів загальновиробничих та загальногосподарських витрат, капітального ремонту, списання матеріалів на обсяг виробництва продукції або будівельних матеріалів, на обсяг виконаних будівельно-монтажних робіт 13. Нормативні перевірки Застосовуються аудитором для отримання доказів про виконання певного завдання. На підставі цих даних аудитор оцінює дотримання показників і розробляє пропозиції, які ...
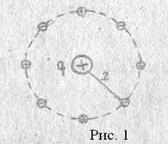
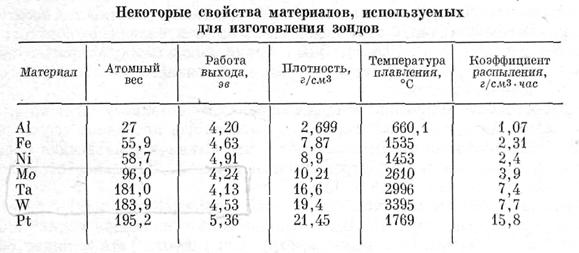
... до спеціальних керамічних матеріалів, таких, як спеченний окис алюмінію і різні сполуки магнію, кремнію і цирконію у випадку гарячих плазм. 2. Потенціал електростатичного зонду в плазмовому гетерогенному середовищі. Зазвичай лінійні розміри зондів, що використовуються для діагностики запиленої плазми лежать в інтервалі [0.1, 10.0] мм та помітно перевищують як дебаєвську довжину електронного ...
... программного обеспечения: критерии, оценки, метод выбора // НТУУ КПІ, 2005, VII МНПК “Системний аналіз та інформаційні технології”, Київ, 2005. С.189. АНОТАЦІЯ Дідковська М. В. Методи оцінки та засоби підвищення надійності програмного забезпечення. – Рукопис. Дисертація на здобуття наукового ступеня кандидата технічних наук за спеціальністю 05.13.06 – “Автоматизовані системи управління та ...
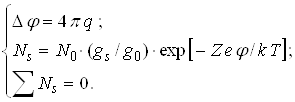
0 комментариев